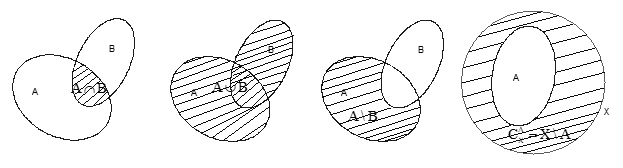
Bài viết trình bày các phép toán trên tập hợp: giao của hai tập hợp, hợp của hai tập hợp, hiệu của hai tập hợp và phần bù của tập hợp
1. Phép giao
A∩B={x∈A và x∈B} hay x∈A∩B⇔{x∈Ax∈B
Ví dụ: Cho tập A={1;4;3},B={1;2} thì A∩B={1}
2. Phép hợp
A∪B={x|x∈Ahayx∈B} hay x∈A∪B⇔[x∈Ax∈B
Ví dụ: Cho tập A={1;4;3},B={1;2} thì A∪B={1;2;3;4}
3. Hiệu của hai tập hợp
A∖B={x∈A và x∉B} hay x∈A∖B⇔{x∈Ax∉B
Ví dụ: Cho tập A={1;4;3},B={1;2} thì A∖B={3;4} và B∖A={2}
A∖B⊂A,B∖A⊂B
4. Phần bù
Cho tập A⊂X, khi đó phần bù của A trong X là X∖A, kí hiệu là CXA.
Vậy CXA=X∖A={x|x∈X và x∉A}
Ví dụ: Cho tập A={1;4;3},B={1;3} thì CAB=A∖B={4}