I. Các khái niệm cơ bản
- Mặt cầu ngoại tiếp hình đa diện nếu nó đi qua mọi đỉnh của đa diện.
- Mặt cầu nội tiếp hình đa diện nếu nó tiếp xúc với mọi mặt của đa diện.
- Trục đa giác đáy là đường thẳng đi qua tâm đường tròn ngoại tiếp đa giác đáy và vuông góc với mặt phẳng chứa đa giác đáy.
+ Mọi điểm nằm trên trục đa giác đáy thì cách đều các đỉnh của đa giác đáy và ngược lại.
- Mặt phẳng trung trực của đoạn thẳng: là mặt phẳng đi qua trung điểm của đoạn thẳng và vuông góc với đoạn
thẳng đó.
+ Mọi điểm nằm trên mặt phẳng trung trực của đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng và ngược lại.
II. Mặt cầu nội, ngoại tiếp một số đa diện cơ bản
- Hình hộp chữ nhật có mặt cầu ngoại tiếp, hình lập phương có cả mặt cầu ngoại tiếp và mặt cầu nội tiếp.

- Hình chóp nội tiếp được mặt cầu nếu và chỉ nếu đáy của nó là đa giác nội tiếp được đường tròn.
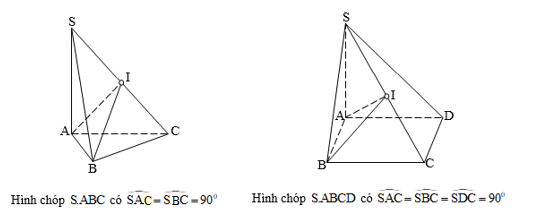
+ Hình chóp có các đỉnh nhìn đoạn thẳng nối hai đỉnh còn lại dưới một góc vuông.
- Hình chóp đều:
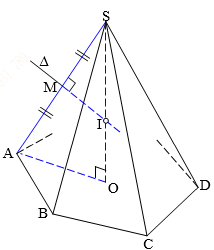
Bán kính: \(R = \dfrac{{{b^2}}}{{2h}}\) với \(b\) là độ dài cạnh bên,
\(h\) là chiều cao hình chóp.
- Hình chóp có cạnh bên vuông góc với đáy:
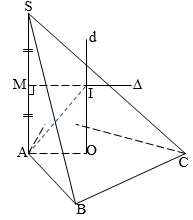
Bán kính \(R = \sqrt {{r^2} + \dfrac{{{h^2}}}{4}} \) với \(r\) là bán kính đường tròn đáy, \(h\) là chiều cao hình chóp.
Đặc biệt: tứ diện vuông: \(R = \sqrt {\dfrac{{{a^2} + {b^2} + {c^2}}}{4}} \) với \(a,b,c\) là ba cạnh bên xuất phát từ đỉnh các góc vuông.
- Lăng trụ nội tiếp được mặt cầu nếu nó là lăng trụ đứng và đáy là đa giác nội tiếp được đường tròn.
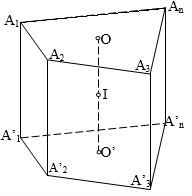
Bán kính \(R = \sqrt {{r^2} + \dfrac{{{h^2}}}{4}} \) với \(r\) là bán kính đường tròn đáy, \(h\) là chiều cao lăng trụ đứng.
III. Công thức tính diện tích mặt cầu, thể tích khối cầu
Cho mặt cầu \(\left( S \right)\) có bán kính \(R\), khi đó:
- Công thức tính diện tích mặt cầu: \(S = 4\pi {R^2}\)
- Công thức tính thể tích khối cầu: \(V = \dfrac{4}{3}\pi {R^3}\)

