Bài viết trình bày dạng hàm số bậc ba và các bước khảo sát hàm số đa thức bậc ba.
Hàm số bậc ba: \(y = a{x^3} + b{x^2} + cx + d\left( {a \ne 0} \right)\)
+) TXĐ: $D = R$
+) Sự biến thiên:
\(y' = 3a{x^2} + 2bx + c\)
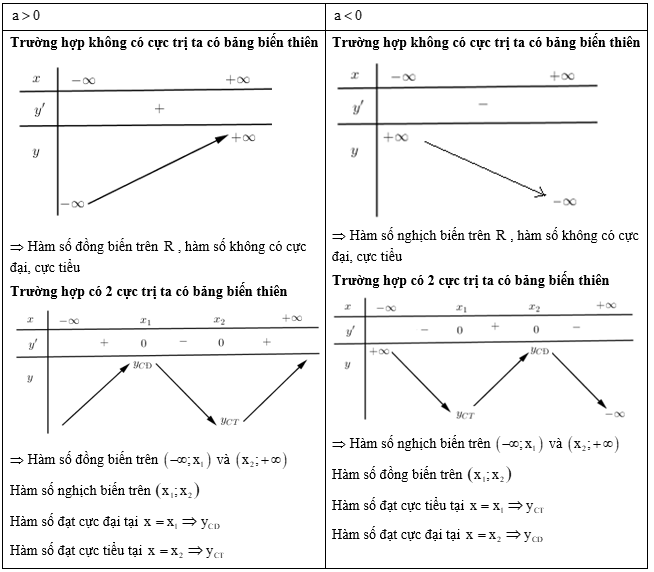
\(y' = 0\) có hai nghiệm phân biệt \({x_1},{x_2} \Rightarrow \) có cực trị.
\(y' = 0\) vô nghiệm hoặc có nghiệm kép \( \Rightarrow \) không có cực trị.
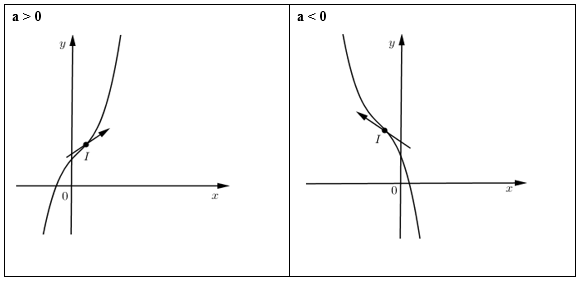
+) Đồ thị:
- Điểm uốn \(I\left( {{x_0};{y_0}} \right)\) với \({x_0}\) là nghiệm của phương trình \(y'' = 0\) và \({y_0} = f\left( {{x_0}} \right)\).
TH1: \(y' = 0\) có hai nghiệm phân biệt \( \Leftrightarrow \Delta ' = {b^2} - 3ac > 0\)
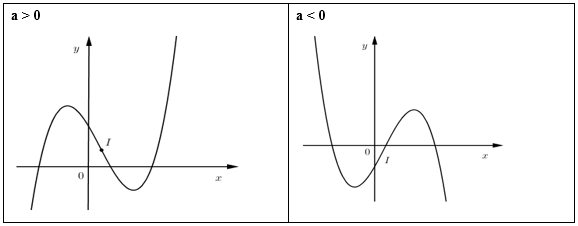
TH2:\(y' = 0\) có nghiệm kép \( \Leftrightarrow \Delta ' = {b^2} - 3ac = 0\)
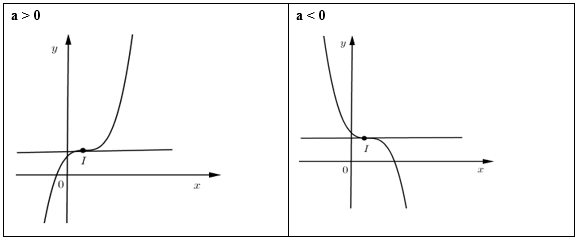
TH3: \(y' = 0\) vô nghiệm \( \Leftrightarrow \Delta ' = {b^2} - 3ac < 0\)