I. Công thức tính diện tích hình phẳng
- Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f(x), trục Ox và hai đường thẳng x=a,x=b(a<b):
S=b∫a|f(x)|dx
- Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f(x),y=g(x) và hai đường thẳng x=a,x=b(a<b):
S=b∫a|f(x)−g(x)|dx
II. Tính diện tích hình phẳng khi biết hai đường giới hạn
Phương pháp:
- Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f(x), trục Ox và hai đường thẳng x=a,x=b(a<b):
Công thức:
S=b∫a|f(x)|dx
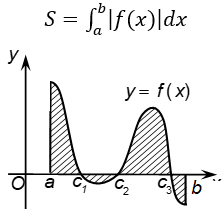
Các bước thực hiện:
+ Bước 1: Gọi S là diện tích cần xác định, ta có: S=∫ba|f(x)|dx.
+ Bước 2: Xét dấu biểu thức f(x) trên [a;b]. Từ đó phân được đoạn [a;b] thành các đoạn nhỏ, giả sử: [a;b]=[a;c1]∪[c1;c2]∪…∪[ck;b] mà trên mỗi đoạn f(x) chỉ có một dấu.
+Bước 3: S=∫c1a|f(x)|dx+∫c2c1|f(x)|dx+…+∫bck|f(x)|dx.
Chú ý: Nếu bài toán phát biểu dưới dạng: "Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số x=f(y) (liên tục trên đoạn [a;b] ) hai đường thẳng y=a,y=b và trục Oy", khi đó công thức tính diện tích là: S=∫ba|f(y)|dy.
- Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f(x),y=g(x) và hai đường thẳng x=a,x=b(a<b):
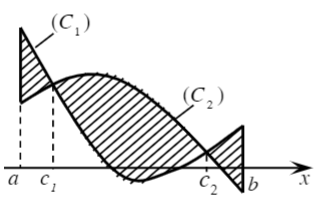
Công thức:
S=b∫a|f(x)−g(x)|dx
Ví dụ: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y=x+1x−2 và các trục tọa độ. Chọn kết quả đúng nhất.
A. 3ln6
B. 3ln32
C. 3ln32−2
D.3ln32−1
Giải:
Đồ thị hàm số cắt Ox tại (−1;0), cắt Oy tại (0;−12).
Hàm số y=x+1x−2 có y′=−3(x−2)2<0,∀x∈(−1;0) nên hàm số y=x+1x−2 nghịch biến trên (−1;0).
Do đó y<0,∀x∈(−1;0)
Do đó S=0∫−1|x+1x−2|dx=0∫−1(−x+1x−2)dx=−0∫−1(1+3x−2)dx
=−(x+3ln|x−2||0−1)=−3ln2−1+3ln3=3ln32−1
Chọn D.
III. Tính diện tích hình phẳng nếu chưa biết hai đường giới hạn
Phương pháp:
- Bước 1: Giải phương trình f(x)=g(x) tìm nghiệm.
- Bước 2: Phá dấu giá trị tuyệt đối của biểu thức |f(x)−g(x)|
- Bước 3: Tính diện tích hình phẳng theo công thức tích phân:
S=b∫a|f(x)−g(x)|dx

