I. Định nghĩa
Hai mặt phẳng gọi là vuông góc với nhau nếu góc giữa chúng bằng \({90^0}\).
Kí hiệu \(\left( P \right) \bot \left( Q \right)\).
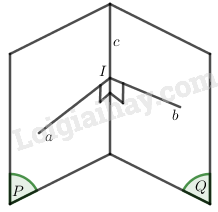
II. Điều kiện để hai mặt phẳng vuông góc
Nếu một mặt phẳng chứa một đường thẳng vuông góc với một mặt phẳng khác thì hai mặt phẳng vuông góc với nhau.
Kí hiệu: \(\left\{ \begin{array}{l}a \bot \left( Q \right)\\a \subset \left( P \right)\end{array} \right. \Rightarrow \left( P \right) \bot \left( Q \right)\)
III. Tính chất
- Nếu hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này vuông góc với giao tuyến đều vuông góc với mặt phẳng kia.
Kí hiệu: \(\left\{ \begin{array}{l}\left( P \right) \bot \left( Q \right)\\\left( P \right) \cap \left( Q \right) = d\\a \subset \left( Q \right)\\a \bot d\end{array} \right. \Rightarrow a \bot \left( P \right)\)
- Nếu hai mặt phẳng \(\left( P \right),\left( Q \right)\) vuông góc với nhau và \(A \in \left( P \right)\) thì đường thẳng \(a\) qua \(A\) và vuông góc với \(\left( Q \right)\) sẽ nằm trong \(\left( P \right)\).
Kí hiệu: \(\left\{ \begin{array}{l}\left( P \right) \bot \left( Q \right)\\A \in \left( P \right)\\a \bot \left( Q \right)\\A \in a\end{array} \right. \Rightarrow a \subset \left( P \right)\)
- Nếu hai mặt phẳng cắt nhau và cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng cũng vuông góc với mặt phẳng thứ ba.
Kí hiệu: \(\left\{ \begin{array}{l}\left( P \right) \cap \left( Q \right) = a\\\left( P \right) \bot \left( R \right)\\\left( Q \right) \bot \left( R \right)\end{array} \right. \Rightarrow a \bot \left( R \right)\)
- Qua đường thẳng \(a\) không vuông góc với mặt phẳng \(\left( Q \right)\), có duy nhất một mặt phẳng \(\left( P \right)\) vuông góc với \(\left( Q \right)\).
IV. Chứng minh hai mặt phẳng vuông góc
Phương pháp chung:
Tìm một đường thẳng \(a\) nằm trong mặt phẳng \(\left( P \right)\) mà \(a \bot \left( Q \right)\).
Ví dụ: Cho tứ diện \(ABCD\) có \(AB \bot \left( {BCD} \right)\). Gọi \(E\) là hình chiếu của \(B\) trên \(CD\). Chứng minh \(\left( {ABE} \right) \bot \left( {ACD} \right)\).
Giải:
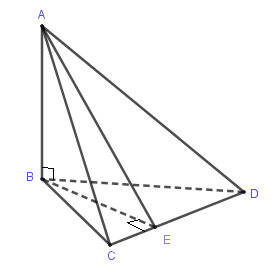
Để chứng minh \(\left( {ACD} \right) \bot \left( {ABE} \right)\) ta sẽ tìm một đường thẳng trong mặt phẳng này mà nó vuông góc với mặt phẳng kia.
Thật vậy,
Ta có: \(AB \bot \left( {BCD} \right) \Rightarrow AB \bot CD\).
Lại có \(BE \bot CD\) nên \(CD \bot \left( {ABE} \right)\).
Mà \(CD \subset \left( {ACD} \right)\) nên \(CD\) chính là đường thẳng nằm trong mặt phẳng \(\left( {ACD} \right)\) mà vuông góc với \(\left( {ABE} \right)\).
Vậy \(\left( {ACD} \right) \bot \left( {ABE} \right)\).
V. Chứng minh đường thẳng vuông góc mặt phẳng
Phương pháp chung:
Ngoài một số phương pháp đề cập từ bài trước, ta có thể sử dụng thêm một trong các phương pháp dưới đây:
+) Chứng minh \(a \subset \left( Q \right)\) với \(\left( Q \right) \bot \left( P \right)\) và \(a\) vuông góc với giao tuyến của \(\left( P \right)\) và \(\left( Q \right)\).
+) Chứng minh \(a\) là giao tuyến của hai mặt phẳng \(\left( Q \right),\left( R \right)\) mà cùng vuông góc với \(\left( P \right)\).

