Góc giữa hai mặt phẳng

I. Cách xác định góc giữa hai mặt phẳng

TH1: Hai mặt phẳng $\left( P \right),\left( Q \right)$ song song hoặc trùng nhau thì góc giữa chúng bằng ${0^0}$.

TH2: Hai mặt phẳng $\left( P \right),\left( Q \right)$ không song song hoặc trùng nhau.

Cách 1:

+) Dựng hai đường thẳng $n,p$ lần lượt vuông góc với hai mặt phẳng $\left( P \right)$ và $\left( Q \right)$.

+) Khi đó, góc giữa hai mặt phẳng $\left( P \right)$ và $\left( Q \right)$ là góc giữa hai đường thẳng $n,p$.

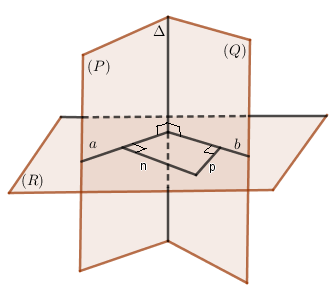
Cách 2:

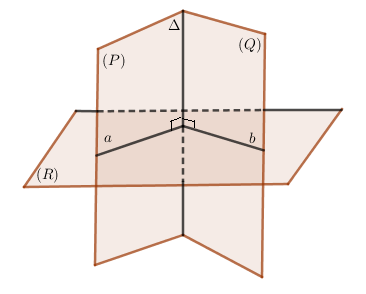
+) Xác định giao tuyến $\Delta$ của hai mặt phẳng $\left( P \right),\left( Q \right)$.

+) Tìm một mặt phẳng $\left( R \right)$ vuông góc $\Delta$ và cắt và hai mặt phẳng theo các giao tuyến $a,b$.

+) Góc giữa hai mặt phẳng $\left( P \right),\left( Q \right)$ là góc giữa $a$ và $b$.

II. Diện tích hình chiếu của đa giác

Gọi $S$ là diện tích của đa giác $\left( H \right)$ trong $\left( P \right),S'$ là diện tích hình chiếu $\left( {H'} \right)$ của $\left( H \right)$ trên mặt phẳng $\left( Q \right)$ và $\alpha  = \left( {\left( P \right),\left( Q \right)} \right)$. Khi đó:

Ví dụ: Cho tứ diện $ABCD$ có $\Delta BCD$ vuông cân tại $B$, $AB \bot \left( {BCD} \right),BC = BD = a$, góc giữa $\left( {ACD} \right)$ và $\left( {BCD} \right)$ là ${30^0}$. Tính diện tích toàn phần của tứ diện $ABCD$.

Giải:

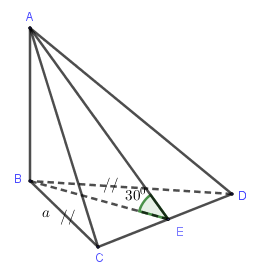
- Xác định góc giữa hai mặt phẳng $\left( {ACD} \right)$ và $\left( {BCD} \right)$:

Ta có: $\Delta ABC = \Delta ABC\left( {c.g.c} \right) \Rightarrow AC = AD$ (cạnh tương ứng)

Gọi $E$ là trung điểm của $CD \Rightarrow AE \bot CD,BE \bot CD$.

Ta có: $\left\{ \begin{array}{l}\left( {ACD} \right) \cap \left( {BCD} \right) = CD\\AE \bot CD\\BE \bot CD\end{array} \right.$  nên góc giữa hai mặt phẳng $\left( {ACD} \right)$ và $\left( {BCD} \right)$ là góc giữa hai đường thẳng $AE,BE$.

Do đó $\widehat {AEB} = {30^0}$.

- Tính diện tích toàn phần của tứ diện:

Tam giác vuông cân $BCE$ có:

$CD = \sqrt {B{C^2} + B{D^2}}  = a\sqrt 2  \Rightarrow BE = \dfrac{1}{2}CD = \dfrac{1}{2}.a\sqrt 2  = \dfrac{{a\sqrt 2 }}{2}$

Tam giác vuông $ABE$ có $AB = BE.\tan {30^0} = \dfrac{{a\sqrt 2 }}{2}.\dfrac{{\sqrt 3 }}{3} = \dfrac{{a\sqrt 6 }}{6}$

Do đó:

${S_{ABC}} = \dfrac{1}{2}BA.BC = \dfrac{1}{2}.\dfrac{{a\sqrt 6 }}{6}.a = \dfrac{{{a^2}\sqrt 6 }}{{12}}$

${S_{ABD}} = \dfrac{1}{2}BA.BD = \dfrac{1}{2}.\dfrac{{a\sqrt 6 }}{6}.a = \dfrac{{{a^2}\sqrt 6 }}{{12}}$

${S_{BCD}} = \dfrac{1}{2}BC.BD = \dfrac{{{a^2}}}{2}$

${S_{ACD}} = \dfrac{{{S_{BCD}}}}{{\cos {{30}^0}}} = \dfrac{1}{2}{a^2}:\dfrac{{\sqrt 3 }}{2} = \dfrac{{{a^2}}}{{\sqrt 3 }} = \dfrac{{{a^2}\sqrt 3 }}{3}$

Vậy diện tích toàn phần của tứ diện là:

$S = {S_{ABC}} + {S_{ABD}} + {S_{BCD}} + {S_{ACD}} = \dfrac{{{a^2}\sqrt 6 }}{{12}} + \dfrac{{{a^2}\sqrt 6 }}{{12}} + \dfrac{{{a^2}\sqrt 3 }}{3} + \dfrac{{{a^2}}}{2} = \dfrac{{{a^2}\left( {\sqrt 6  + 2\sqrt 3  + 3} \right)}}{6}$ .