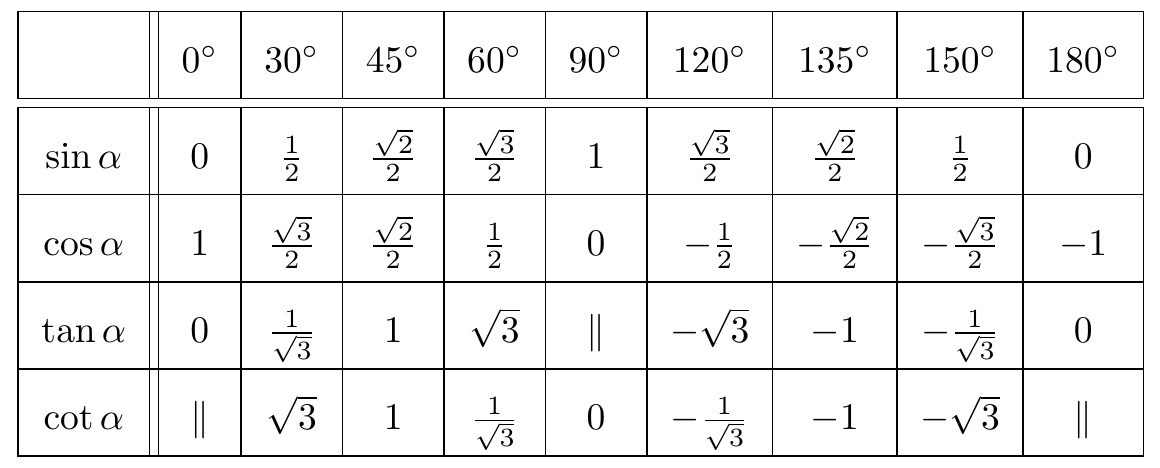
I. Giá trị lượng giác sin, cos, tan, cot
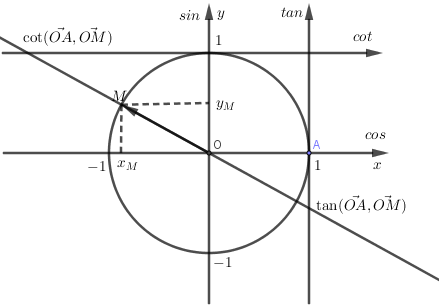
Tính chất:
\(\sin \alpha ,\,\cos \alpha \) xác định với mọi giá trị của \(\alpha \) và \( - 1 \le \sin \alpha \le 1,\, - 1 \le \cos \alpha \le 1\).
\(\tan \alpha \) được xác định khi \(\alpha \ne \dfrac{\pi }{2} + k\pi \), \(\cot \alpha \) xác định khi \(\alpha \ne k\pi \)
\(\sin \alpha = \sin \left( {\alpha + k2\pi } \right),\,\cos \alpha = \cos \left( {\alpha + k2\pi } \right)\)
\(\tan \alpha = \tan \left( {\alpha + k\pi } \right),\,\cot \alpha = \cot \left( {\alpha + k\pi } \right)\)
Bảng xét dấu giá trị lượng giác của một góc, cung lượng giác
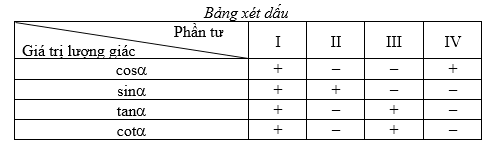
II. Các hệ thức lượng giác cơ bản
\(\begin{array}{l}1){\sin ^2}\alpha + {\cos ^2}\alpha = 1\\2)\tan \alpha = \dfrac{{\sin \alpha }}{{\cos \alpha }}\left( {\alpha \ne \dfrac{\pi }{2} + k\pi } \right)\\3)\cot \alpha = \dfrac{{\cos \alpha }}{{\sin \alpha }}\left( {\alpha \ne k\pi } \right)\\4)1 + {\tan ^2}\alpha = \dfrac{1}{{{{\cos }^2}\alpha }}(\alpha \ne \dfrac{\pi }{2} + k\pi )\\5)1 + {\cot ^2}\alpha = \dfrac{1}{{{{\sin }^2}\alpha }}(\alpha \ne k\pi )\\6)\tan \alpha .\cot \alpha = 1(\alpha \ne \dfrac{{k\pi }}{2})\end{array}\)
III. Giá trị lượng giác của một góc
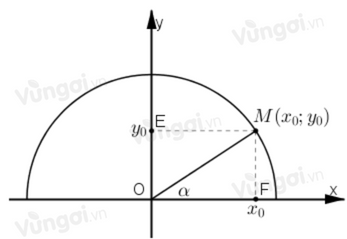
- Sin của góc \(\alpha \), kí hiệu là \(\sin \alpha \), được xác định bởi: \(\sin \alpha = {y_0}\);
- Côsin của góc \(\alpha \), kí hiệu là \(\cos \alpha \), được xác định bởi: \(\cos \alpha = {x_0}\);
- Tang của góc \(\alpha \), kí hiệu là tan \(\alpha \), được xác định bởi: \(\tan \alpha = \dfrac{{{y_0}}}{{{x_0}}}\left( {{x_0} \ne 0} \right)\);
- Côtang của góc \(\alpha \), kí hiệu là \(\cot \alpha \), được xác định bởi: \(\cot \alpha = \dfrac{{{x_0}}}{{{y_0}}}\left( {{y_0} \ne 0} \right)\).
Các số \(\sin \alpha ,\cos \alpha ,\tan \alpha ,\cot \alpha \) được gọi là các giá trị lượng giác của góc \(\alpha \).
Bảng giá trị lượng giác của một số góc đặc biệt: