I. Thể tích và tỉ số thể tích của khối chóp
a) Thể tích khối chóp
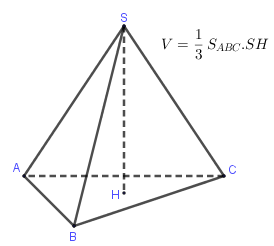
- Thể tích khối chóp: \(V = \dfrac{1}{3}Sh\) với \(S\) là diện tích đáy, \(h\) là chiều cao.
- Một phép vị tự tỉ số \(k\) biến khối đa diện có thể tích $V$ thành khối đa diện có thể tích \(V'\) thì: \(\dfrac{{V'}}{V} = {\left| k \right|^3}\)
b) Tỉ số thể tích hai khối chóp tam giác
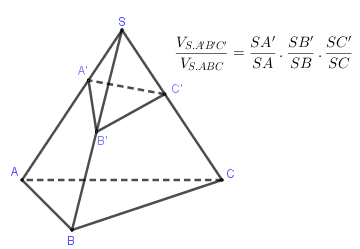
Nếu \(A',B',C'\) là ba điểm lần lượt nằm trên các cạnh \(SA,SB,SC\) của hình chóp tam giác \(S.ABC\). Khi đó:
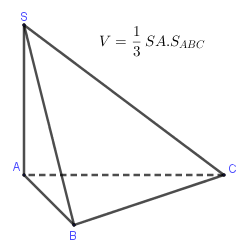
II. Tính thể tích khối chóp có cạnh bên vuông góc với đáy
Cho khối chóp $S.ABC$ có cạnh bên $SA$ vuông góc với $(ABC)$
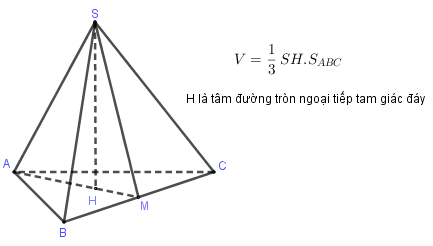
III. Tính thể tích khối chóp đều
Hình chóp đều là hình chóp có đáy là đa giác đều và chân đường cao là tâm của đáy.
IV. Tính thể tích khối chóp có mặt bên vuông góc với đáy
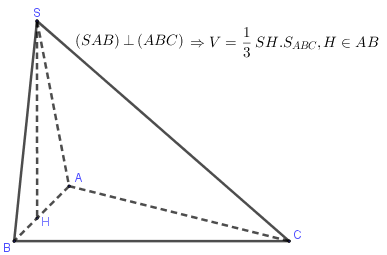
V. Tính tỉ lệ thể tích các khối chóp.
Phương pháp:
- Bước 1: Chia các khối chóp cần tính tỉ lệ thể tích thành các khối chóp tam giác tương ứng với nhau.
- Bước 2: Áp dụng công thức tính tỉ số thể tích các khối chóp \(\dfrac{{{V_{S.A'B'C'}}}}{{{V_{S.ABC}}}} = \dfrac{{SA'}}{{SA}}.\dfrac{{SB'}}{{SB}}.\dfrac{{SC'}}{{SC}}\), ở đó \(A' \in SA,B' \in SB,C' \in SC\)
Một số công thức tính thể tích khối tứ diện thường gặp trong đề thi
- Tứ diện đều cạnh \(a\): \(V = \dfrac{{{a^3}\sqrt 2 }}{{12}}\).
- Tứ diện vuông (các góc tại một đỉnh của tứ diện là góc vuông):
Tứ diện \(ABCD\) có \(AB,AC,AD\) đôi một vuông góc và \(AB = a,AC = b,AD = c\) ta có \(V = \dfrac{1}{6}abc\).
- Công thức tính thể tích sử dụng các độ dài, khoảng cách và góc giữa hai cạnh đối diện của tứ diện:
Tứ diện \(ABCD\) có \(AD = a,BC = b\), khi đó: \(V = \dfrac{1}{6}ab.\sin \left( {AD,BC} \right).d\left( {AD,BC} \right)\)
- Tứ diện gần đều (các cặp cạnh đối tương ứng bằng nhau):
Tứ diện \(ABCD\) có \(AB = CD = a;BC = AD = b;AC = BD = c\) ta có:
\(V = \dfrac{{\sqrt {2} }}{{12}}\sqrt {\left( {{a^2} + {b^2} - {c^2}} \right)\left( {{b^2} + {c^2} - {a^2}} \right)\left( {{a^2} + {c^2} - {b^2}} \right)} \)

