I. Tính thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi một đồ thị quanh trục Ox
Bài toán: Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng (H) giới hạn bởi đồ thị hàm số y=f(x), trục Ox (y=0) và hai đường thẳng x=a,x=b(a<b) quanh trục Ox
- Nếu thiếu cận thì giải phương trình f(x)=0 để bổ sung cận.
- Công thức tính:
V=πb∫af2(x)dx
Ví dụ: Cho đường cong y=−x2+1 và đường thẳng y=0. Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi hai đường trên quanh Ox.
Ta có: −x2+1=0⇔[x=−1x=1
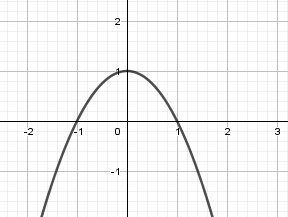
Thể tích: V=π1∫−1(−x2+1)2dx=π1∫−1(x4−2x2+1)dx
=π(x55−2x33+x)|1−1=16π15.
II. Tính thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi một đồ thị quanh trục Oy
Bài toán: Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng (H) giới hạn bởi đồ thị hàm số x=f(y), trục Oy và hai đường thẳng y=a,y=b(a<b) quanh trục Oy.
- Giải phương trình f(y)=0 để bổ sung cận.
- Công thức tính:
V=πb∫af2(y)dy
III. Tính thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi hai đồ thị quanh trục Ox
Bài toán: Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng (H) giới hạn bởi các đồ thị hàm số y=f(x),y=g(x) liên tục trên [a;b],0≤f(x)≤g(x),∀x∈[a;b] quay quanh trục Ox
Công thức tính:
V=πb∫a[g2(x)−f2(x)]dx
IV. Tính thể tích của vật thể biết diện tích thiết diện cắt bởi các mặt phẳng vuông góc với Ox
Bài toán: Tính thể tích của vật thể giới hạn bởi các mặt phẳng x=a,x=b biết diện tích thiết diện cắt bởi mặt phẳng vuông góc trục Ox là S=S(x).
Công thức tính:
V=b∫aS(x)dx
Khi miền D giới hạn bởi nhiều đồ thị hàm số thì ta nên vẽ hình, sau đó từ hình vẽ suy ra cách tính.

