Giải bài toán bằng cách lập hệ phương trình

Gọi số cần tìm là \(\overline {ab} ,\,\,a \in {\mathbb{N}^*},\,\,b \in {\mathbb{N}^*}\), $a,b \le 9$.

Đổi chỗ hai chữ số của nó thì được một số mới là \(\overline {ba} \)

Ta có hệ phương trình :

\(\left\{ \begin{array}{l}\overline {ba}  - \overline {ab}  = 63\\\overline {ba}  + \overline {ab}  = 99\end{array} \right. \Rightarrow \left\{ \begin{array}{l}2\overline {ab}  = 36\\\overline {ba}  + \overline {ab}  = 99\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\overline {ab}  = 18\\\overline {ba}  = 81\end{array} \right.\,\)(thỏa mãn)

Vậy số cần tìm là $18$  nên tổng các chữ số là $1 + 8 = 9$.

Gọi số cần tìm là \(\overline {ab} ,\,\,a \in {\mathbb{N}^*},\,\,b \in {\mathbb{N}^*}\), $a,b \le 9$.

Đổi chỗ hai chữ số của nó thì được một số mới là \(\overline {ba} \)

Ta có hệ phương trình :

$\left\{ \begin{array}{l}a - b = 5\\\overline {ba}  = \dfrac{3}{8}\overline {ab} \end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}a = b + 5\\b.10 + a = \dfrac{3}{8}\left( {a.10 + b} \right)\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}a = b + 5\\80b + 8\left( {b + 5} \right) = 30\left( {b + 5} \right) + 3b\end{array} \right.$

$ \Leftrightarrow \left\{ \begin{array}{l}a = b + 5\\55b = 110\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 2\\a = 7\end{array} \right.$(thỏa mãn)

Vậy số cần tìm là $72$ nên tích các chữ số là $2.7 = 14$.

Gọi số tiền mà người thứ nhất, thứ hai, thứ ba thứ tư trả lần lượt là \(x,y,z,t\left( {x,y,z,t \in {\mathbb{N}^*}} \right)\).

Theo đề bài ta có hệ: \(\left\{ \begin{array}{l}x + y + z + t = 60.000\\y = \dfrac{1}{2}\left( {y + z + t} \right)\\z = \dfrac{1}{3}\left( {x + y + t} \right)\\t = \dfrac{1}{4}\left( {x + y + z} \right)\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}x + y + z + t = 60.000\\2y = x + t + z\\3z = x + y + t\\4t = x + y + z\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 13.000\\y = 20.000\\z = 15.000\\t = 12.000\end{array} \right.\)

Vậy người thứ nhất trả 13.000 đồng.

Gọi thời gian ô tô đi trên mỗi đoạn đường $AB$ và $BC$ lần lượt là $x,y$

($x>0;y>0,5$ ; đơn vị : giờ). Ta có hệ phương trình :

\(\left\{ \begin{array}{l}50.x + 45.y = 165\\y - x = 0,5\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = 1,5\\y = 2\end{array} \right.\) (Thỏa mãn)

Vậy thời gian ô tô đi hết quãng đường $AB$ là $1,5$ giờ. Thời gian ô tô đi hết quãng đường $BC$ là $2$  giờ.

Bước 1:

Gọi số tiền mua 1 quyển tập, 1 bút bi, 1 bút chì lần lượt là: \(x;y;z\left( {x;y;z > 0} \right)\) (nghìn đồng).

Bước 2:

Theo bài ta có hệ:

\(\begin{array}{l}\left\{ \begin{array}{l}2x + 2y + 3z = 68000\\3x + 2y + 4z = 74000\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}6x + 6y + 9z = 204000\\6x + 4y + 8z = 148000\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}2y + z = 56000\\3x = 74000 - \left( {2y + 4z} \right)\end{array} \right.\end{array}\)

Bước 3:

Số tiền bạn C phải trả là:

\(\begin{array}{l}3x + 4y + 5z = 74000 - \left( {2y + 4z} \right)+ 4y + 5z\\ = 74000 + 2y + z = 74000 + 56000\\ = 130000\end{array}\)

Vậy số tiền bạn C phải trả là 130.000 đồng.

Gọi năng suất lúa mới và lúa cũ trên $1$ ha lần lượt là $x;y\,\,\left( {x,y > 0} \right)$ đơn vị: tấn/ha

Vì cấy $60$ ha lúa giống mới và $40$  ha lúa giống cũ, thu hoạch được tất cả $460$  tấn thóc nên ta có

$60x + 40y = 460$

 Vì $3$ ha trồng lúa mới thu hoạch được ít hơn $4$ ha trồng lúa cũ là $1$  tấn nên ta có phương trình

$4y - 3x = 1$

Suy ra hệ phương trình $\left\{ \begin{array}{l}4y - 3x = 1\\60x + 40y = 460\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 30x + 40y = 10\\60x + 40y = 460\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 5\\y = 4\end{array} \right.$ (thỏa mãn)

Vậy năng suất  lúa mới trên $1$  ha là $5$ tấn.

Bước 1:

Gọi năng suất lúa mới và lúa cũ trên 1 ha lần lượt là $x;y (x;y>0)$, (tấn/ha)

Bước 2:

Vì cấy 60 (ha) lúa giống mới và 40 (ha) lúa giống cũ, thua hoạch được tất cả 460 tấn thóc nên ta có phương trình:

\(60x + 40y = 460\)

Bước 3:

Vì 3 (ha) trồng lúa mới thu hoạch được ít hơn 4 (ha) trồng lúa cũ là 1 tấn nên ta có phương trình \(4y - 3x = 1\).

Bước 4:

Khi đó ta có hệ phương trình \(\left\{ \begin{array}{l} - 3x + 4y = 1\\60x + 40y = 460\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 5\\y = 4\end{array} \right.\left( {tm} \right)\)

Vậy năng suất lúa mới trên 1 ha là 5 tấn.

Bước 1:

Gọi số trâu đứng, trâu nằm, trâu già lần lượt là \(x,y,z\) (con), \(\left( {0 < x,y,z < 100;x,y,z \in \mathbb{N}} \right)\), (\(y\) là số lẻ).

Bước 2:

Theo đề bài,

Tổng số con trâu là 100 nên ta có: \(x + y + z = 100\left( 1 \right)\).

Trâu đứng ăn năm tức là mỗi con trâu đứng ăn 5 bó

Trâu nằm ăn ba tức là mỗi con trâu nằm ăn 3 bó.

Trâu già, ba con 1 bó tức là cứ 3 con bò thì ăn hết 1 bó.

=> Ta có phương trình tương ứng về tổng số bó cỏ là \(5x + 3y + \dfrac{1}{3}z = 100\).

Từ (1), (2) ta được hệ: \(\left\{ \begin{array}{l}x + y + z = 100\\5x + 3y + \dfrac{1}{3}z = 100\end{array} \right.\)

Bước 3:

\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}x + y + z = 100\\15x + 9y + z = 300\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x + y + z = 100\\14x + 8y = 200\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x + y + z = 100\\7x + 4y = 100\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x + y + z = 100\\y = \dfrac{{100 - 7z}}{4}\end{array} \right.\end{array}\)

Ta có \(y = \dfrac{{100 - 7x}}{4} = 25 - \dfrac{{7x}}{4}\) là số lẻ nên \(x \vdots 4,\dfrac{{7x}}{4} < 25\) và \(\dfrac{{7x}}{4}\) chẵn.

\(\dfrac{{7x}}{4} < 25 \Leftrightarrow x < \dfrac{{100}}{7} \Rightarrow x \le 14\)

Do \(x \vdots 4 \Rightarrow x \in \left\{ {4;8;12} \right\}\)

Với \(x = 4 \Rightarrow \dfrac{{7x}}{4} = 7\)(KTM).

Với \(x = 8\)\( \Rightarrow \dfrac{{7x}}{4} = 14\)(TM)

=> \(y = 25 - 14 = 11\)

Với \(x = 12 \Rightarrow \dfrac{{7x}}{4} = 21\)(KTM).

Vậy số trâu nằm là 11 con.

Bước 1:

Gọi thời gian người A, người B, người C làm một mình xong công việc lần lượt là \(x,y,z\) (giờ), \(\left( {x,y,z > 0} \right)\).

Bước 2:

Mỗi giờ người A, B, C làm được công việc lần lượt là \(\dfrac{1}{x},\dfrac{1}{y},\dfrac{1}{z}\) (công việc).

Theo đề bài,

Hai người A và B cùng làm xong công việc trong 72 giờ nên ta có: \(\dfrac{1}{x} + \dfrac{1}{y} = \dfrac{1}{{72}}\).

Người A và C cùng làm xong công việc trong 63 giờ nên ta có: \(\dfrac{1}{x} + \dfrac{1}{z} = \dfrac{1}{{63}}\).

Người B và C cùng làm xong công việc trong 56 giờ nên ta có: \(\dfrac{1}{y} + \dfrac{1}{z} = \dfrac{1}{{56}}\)

=> Ta được hệ: \(\left\{ \begin{array}{l}\dfrac{1}{x} + \dfrac{1}{y} = \dfrac{1}{{72}}\\\dfrac{1}{x} + \dfrac{1}{z} = \dfrac{1}{{63}}\\\dfrac{1}{y} + \dfrac{1}{z} = \dfrac{1}{{56}}\end{array} \right.\)

Bước 3:

=> Trong một giờ cả ba cùng làm được số công việc là \(\dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z} = \left( {\dfrac{1}{{72}} + \dfrac{1}{{63}} + \dfrac{1}{{56}}} \right):2 = \dfrac{1}{{42}}\)(công việc).

Vậy cả ba cùng làm thì hoàn thành công việc trong \(42\) (giờ).

Bước 1:

Gọi số học sinh của trường thứ nhất dự thi là \(x\) (học sinh) \(\left( {x \in {\mathbb{N}^*},x < 300} \right)\).

Số học sinh của trường thứ hai dự thi là \(y\) (học sinh) \(\left( {y \in {\mathbb{N}^*},y < 300} \right)\).

Hai trường có tất cả 300 học sinh tham gia cuộc thi nên ta có phương trình \(x + y = 300\left( 1 \right)\)

Trường A có 75% học sinh đạt, trường B có 60% đạt nên cả hai trường có 207 học sinh đạt, ta có:

\(0,75x + 0,6y = 207\left( 2 \right)\)

Bước 2:

Từ (1) và (2) ta được hệ:

\(\begin{array}{l}\left\{ \begin{array}{l}x + y = 300\\0,75x + 0,6y = 207\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 180\left( {tm} \right)\\y = 120\left( {tm} \right)\end{array} \right.\end{array}\)

Bước 3:

Vậy số học sinh của trường A dự thi là 180 học sinh, số học sinh của trường B dự thi là 120 học sinh.

Bước 1:

Gọi năng suất của Minh là x (công việc/giờ), năng suất của hai thợ phụ là y (công việc/giờ) và thời gian họ nghỉ ăn trưa là z (giờ) \(\left( {x,y,z > 0} \right)\).

Bước 2:

Thời gian cả 3 người cùng làm việc ngày thứ nhất là \(16 - 8 - z = 8 - z\)(giờ).

Ngày thứ nhất, cả 3 người làm được 50% ngôi nhà nên có phương trình \(\left( {8 - z} \right)\left( {x + y} \right) = \dfrac{{50}}{{100}}\left( 1 \right)\).

Thời gian làm việc của 2 thợ phụ ngày thứ hai (tính cả lúc ăn trưa) là 6 giờ 12 phút = \(\dfrac{{31}}{5}\left( h \right)\).

Thời gian làm việc ngày thứ 2 (không tính lúc ăn trưa) là \(\dfrac{{31}}{5} - z\)(giờ).

Do lượng công việc của hai thợ phụ làm được là 24% ngôi nhà nên ta có: \(\left( {\dfrac{{31}}{5} - z} \right).y = \dfrac{{24}}{{100}}\left( 2 \right)\).

Thời gian Minh làm ngày thứ 3 (không tính lúc ăn trưa) là \(\dfrac{{56}}{5} - z\) (giờ).

Ngày thứ ba Minh làm được 100%-50%-24%=26% ngôi nhà nên ta có phương trình:

\(\left( {\dfrac{{56}}{5} - z} \right).x = \dfrac{{26}}{{100}}\left( 3 \right)\) .

Bước 3:

Lấy (1)-(2)-(3) ta được:

\(\begin{array}{l}\left( {8 - z} \right)\left( {x + y} \right) - \left( {\dfrac{{31}}{5} - z} \right).y - \left( {\dfrac{{56}}{5} - z} \right).x = 0\\ \Leftrightarrow 8\left( {x + y} \right) - \dfrac{{31}}{5}y - \dfrac{{56}}{5}x = 0\\ \Leftrightarrow \dfrac{y}{x} = \dfrac{{16}}{9}\end{array}\)

Lấy (2) chia cho (3) ta được:

\(\begin{array}{l}\dfrac{{\dfrac{{31}}{5} - z}}{{\dfrac{{56}}{5} - z}}.\dfrac{y}{x} = \dfrac{{24}}{{26}} \Leftrightarrow \dfrac{{31 - 5z}}{{56 - 5z}} = \dfrac{{12}}{{13}}.\dfrac{9}{{16}} = \dfrac{{27}}{{52}}\\ \Leftrightarrow z = 0,8\left( {tm} \right)\end{array}\)

Bước 4:

Vậy ba người nghỉ ăn trưa \(0,8\left( h \right) = 48\) phút.

Bước 1:

Gọi số cá của An, Phương, Minh lần lượt là \(x,y,z\left( {0 < x,y,z < 24;x,y,z \in \mathbb{N}} \right)\).

Bước 2:

Ta có bảng sau:

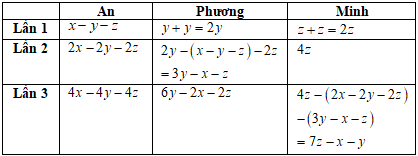
Vì sau lần 3 cả ba bạn có số cá bằng nhau và tổng số cá 3 bạn câu được là 24 con nên sau 3 lần nhường cá thì mỗi bạn có 8 con.

Bước 3:

Ta có hệ: \(\left\{ \begin{array}{l}4x - 4y - 4z = 8\\6y - 2x - 2z = 8\\7z - x - y = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 13\\y = 7\\z = 4\end{array} \right.\left( {tm} \right)\)

Bước 4:

Vậy lúc đầu An câu được 13 con, Phương câu được 7 con và Minh câu được 4 con.

Bước 1: Gọi số học sinh nữ và học sinh nam của lớp học đó là: \(x,y\) (học sinh),\(\left( {x,y \in {\mathbb{N}^*},y < x < 30} \right)\).

Khi đó ta có: \(x + y = 30\)   (1)

Bước 2: Gọi giá tiền của một cái bánh phô mai và một cốc cô-ca lần lượt là \(a,b\) (đô-la), \(\left( {a,b \in {\mathbb{N}^*}} \right)\).

Bước 3:

Số tiền đã tiêu sau giải lao lần thứ nhất là: \(ax + by\) (đô-la).

Số tiền đã tiêu sau giải lao lần thứ hai là: \(ay + bx\) (đô-la).

Lần giải lao thứ hai, cả lớp tiêu ít hơn lần thứ nhất là 2 đô – la nên ta có phương trình:

\(\begin{array}{l}ax + by - \left( {ay + bx} \right) = 2\\ \Leftrightarrow a\left( {x - y} \right) - b\left( {x - y} \right) = 2\end{array}\)

\( \Leftrightarrow \left( {a - b} \right)\left( {x - y} \right) = 2\)

Vì \(a,b,x,y\) đều là các số tự nhiên nên ta có: \(x - y \in \left\{ { \pm 1; \pm 2} \right\}\)

Lại có \(x + y = 30\) là số chẵn nên \(x - y\) cũng phải là số chẵn, mà \(x > y =  > x - y > 0\).

\( \Rightarrow x - y = 2\)   (2)

Từ (1) và (2) ta có \(\left\{ \begin{array}{l}x + y = 30\\x - y = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 16\left( {tm} \right)\\y = 14\left( {tm} \right)\end{array} \right.\)

Vậy lớp đó có 16 bạn nam và 14 bạn nữ.

Bước 1:

Gọi số hộp lớn có chứa hộp nhỡ  là: \(x\) (hộp),\(\left( {x \in {\mathbb{N}^*},x < 11} \right)\).

Gọi số hộp nhỡ có chứa hộp nhỏ  là: \(y\) (hộp),\(\left( {y \in {\mathbb{N}^*},y < 8} \right)\).

Bước 2:

Số hộp nhỡ là \(8x\) (hộp).

Số hộp nhỏ là \(8y\) (hộp).

Số chiếc hộp lớn không chứa các hộp nhỡ là: \(11 - x\) (hộp).

Số chiếc hộp nhỡ không chứa các hộp nhỏ là: \(8x - y\) (hộp).

Theo đề bài ta có 102 cái hộp rỗng nên ta có phương trình:

\(11 - x + 8x - y + 8y = 102 \Leftrightarrow x + y = 13\)

Bước 3:

Tổng số hộp là \(11 + 8x + 8y = 11 + 8\left( {x + y} \right) = 115\) (hộp).

Bước 1:

Gọi số tiền 1 kg cam là \(x\) (đồng) \(\left( {x > 0} \right)\)

Gọi số tiền 1 kg quýt là \(y\) (đồng) \(\left( {y > 0} \right)\)

Gọi số tiền 1 kg táo là \(z\) (đồng) \(\left( {z > 0} \right)\)

Bác Mai mua 2 kg cam, 2 kg quýt và 1 kg táo hết 108.000 đồng nên ta có phương trình:

\(2x + 2y + z = 108000\)   (1)

Cô Loan mua 3 kg cam, 1 kg quýt và 2 kg táo hết 121.000 đồng nên ta có phương trình:

\(3x + y + 2z = 121000\)   (2)

Chị Hà mua 2 kg cam, 3 kg quýt và 1 kg táo hết 133.000 đồng nên ta có phương trình:

\(2x + 3y + z = 133000\)    (3)

Bước 2:

Từ (1), (2) và (3) ta có hệ phương trình:

\(\begin{array}{l}\left\{ \begin{array}{l}2x + 2y + z = 108000\\3x + y + 2z = 121000\\2x + 3y + z = 133000\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 20000\left( {tm} \right)\\y = 25000\left( {tm} \right)\\z = 18000\left( {tm} \right)\end{array} \right.\end{array}\)

Bước 3:

Vậy chị Thu mua 1 kg cam, 4 kg quýt và 2 kg táo thì hết số tiền là

\(1.20000 + 4.25000 + 2.18000 = 156000\) (đồng).

Bước 1:

Gọi độ dài các cạnh góc vuông của \(\Delta ABC\) là \(x,y\left( m \right)\), độ dài cạnh huyền là \(z\left( m \right),\left( {0 < x,y,z < 24} \right)\).

Chu vi của tam giác là \(24\)m nên ta có phương trình \(x + y + z = 24\).

Tổng bình phương của ba cạnh của tam giác là 200 nên ta có: \({x^2} + {y^2} + {z^2} = 200\).

Áp dụng định lý Pitago ta có phương trình: \({x^2} + {y^2} = {z^2}\)

Bước 2:

Vậy ta có hệ \(\left\{ \begin{array}{l}x + y + z = 24\\{x^2} + {y^2} + {z^2} = 200\\{x^2} + {y^2} = {z^2}\end{array} \right.\)\( \Leftrightarrow 2{z^2} = 200 \Leftrightarrow z = 10\left( {tm} \right)\)

Bước 3:

\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}x + y = 14\\{x^2} + {y^2} = 100\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 14 - x\\2{x^2} - 28x + 96 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 6,y = 8\\x = 8,y = 6\end{array} \right.\end{array}\)

Độ dài cạnh huyền của tam giác đã cho là 10 m.

Bước 1:

Gọi vận tốc thực của thuyền và vận tốc của dòng nước lần lượt là \(x,y\left( {km/h} \right),\left( {0 < y < x} \right)\).

Bước 2:

\( \Rightarrow \)Vận tốc của thuyền khi nước xuôi dòng và ngược dòng lần lượt là:

\(x + y\left( {km/h} \right),x - y\left( {km/h} \right)\).

\( \Rightarrow \)Thời gian thuyền đi xuôi dòng và ngược dòng hết  40km  lần lượt là \(\dfrac{{40}}{{x + y}}\left( h \right),\dfrac{{40}}{{x - y}}\left( h \right)\).

Chiếc thuyền đã đi xuôi dòng và ngược dòng khúc sông dài 40 km hết 4 giờ 30 phút = \(\dfrac{9}{2}\left( h \right)\) nên ta có phương trình: \(\dfrac{{40}}{{x + y}} + \dfrac{{40}}{{x - y}} = \dfrac{9}{2}\left( 1 \right)\)

Thời gian thuyền xuôi dòng 5 km là: \(\dfrac{5}{{x + y}}\left( h \right)\)

Thời gian thuyền ngược dòng 4 km là \(\dfrac{4}{{x - y}}\left( h \right)\).

Khi đó ta có phương trình \(\dfrac{5}{{x + y}} = \dfrac{4}{{x - y}}\)  (2)

Bước 3:

Từ (1) và (2) ta có hệ: \(\left\{ \begin{array}{l}\dfrac{{40}}{{x + y}} + \dfrac{{40}}{{x - y}} = \dfrac{9}{2}\\\dfrac{5}{{x + y}} = \dfrac{4}{{x - y}}\end{array} \right.\)

Đặt \(\dfrac{1}{{x + y}} = a,\dfrac{1}{{x - y}} = b\). Khi đó hệ phương trình trên trở thành: \(\left\{ \begin{array}{l}40a + 40b = \dfrac{9}{2}\\5a = 4b\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \dfrac{1}{{20}}\\b = \dfrac{1}{{16}}\end{array} \right.\)

\( \Rightarrow \left\{ \begin{array}{l}x + y = 20\\x - y = 16\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 18\\y = 2\end{array} \right.\left( {tm} \right)\)

Bước 4: Vậy vận tốc dòng nước là 2km/h.

Bước 1:

Gọi số có hai chữ số cần tìm là: \(\overline {ab} \left( {a \in {\mathbb{N}^*},b \in \mathbb{N},0 < a \le 90 \le b \le 9} \right)\).

Bước 2:

Số đảo ngược của số ban đầu là: \(\overline {ba} \left( {b \ne 0} \right)\).

Theo đề bài, hiệu của số ban đầu với số đảo ngược của nó bằng 18 nên ta có:

\(\begin{array}{l}\overline {ab}  - \overline {ba}  = 18\\ \Leftrightarrow 10a + b - 10b - a = 18\\ \Leftrightarrow 9a - 9b = 18\\ \Leftrightarrow a - b = 2\left( 1 \right)\end{array}\)

Tổng của số ban đầu với bình phương số đảo ngược của nó bằng 618 nên ta có:

\(\begin{array}{l}\overline {ab}  + {\left( {\overline {ba} } \right)^2} = 618\\ \Leftrightarrow 10a + b + {\left( {10b + a} \right)^2} = 618\\ \Leftrightarrow 10a + b + 100{b^2} + 20ab + {a^2} = 618\end{array}\)

Bước 3:

Từ (1) và (2) ta có hệ phương trình:

\(\begin{array}{l}\left\{ \begin{array}{l}a - b = 2\\10a + b + 100{b^2} + 20ab + {a^2} = 618\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}a = b + 2\\10\left( {b + 2} \right) + b + 100{b^2} + 20\left( {b + 2} \right)b + \left( {b + 2} \right) = 618\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}a = b + 2\\121{b^2} + 55b - 594 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}a = b + 2\\\left[ \begin{array}{l}b = 2\left( {tm} \right)\\b =  - \dfrac{{27}}{{11}}\left( {ktm} \right)\end{array} \right.\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 4\\b = 2\end{array} \right.\left( {tm} \right)\end{array}\)

Vậy số cần tìm là 42.

Bước 1: Gọi số sách khối 8 và khối 9 quyên góp được lần lượt là \(x,y\) (quyển), \(\left( {0 < x,y < 540;x,y \in \mathbb{N}} \right)\).

Bước 2:

Số sách cả hai khối quyên góp được là: \(x + y = 540\)   (1)

Số sách một bạn học sinh khối 8 quyên góp là: \(\dfrac{x}{{120}}\) (quyển)

Số sách một bạn học sinh khối 9 quyên góp là: \(\dfrac{y}{{100}}\)(quyển)

Mỗi học sinh khối 9 quyên góp nhiều hơn nhiều hơn mỗi học sinh khối 8 một quyển nên ta có phương trình:

\(\dfrac{y}{{100}} - \dfrac{x}{{120}} = 1 \Leftrightarrow  - 5x + 6y = 600\)   (2)

Bước 3:

Từ (1) và (2) ta có hệ phương trình:

\(\left\{ \begin{array}{l}x + y = 540\\ - 5x + 6y = 600\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 240\left( {tm} \right)\\y = 300\left( {tm} \right)\end{array} \right.\)

Vậy khối 9 đã quyên góp được 300 quyên sách, khối 8 quyên góp được 240 quyển.

Bước 1:

Gọi khối lượng kẹo $A, B$ có trong thùng lần lượt là $x, y(kg)$, $x>0,y>0$

Khi đó ta có: $x+y=18$

Một thùng (khi đầy) có thể chứa được 14kg kẹo loại A hoặc 21 kg kẹo loại B nên ta có $\dfrac{x}{14}+\dfrac{y}{21}=1$
Bước 2:

Ta có hệ $\left\{\begin{array}{l}\dfrac{x}{14}+\dfrac{y}{21}=1 \\ x+y=18\end{array} \Leftrightarrow\left\{\begin{array}{l}x=6 \\ y=12\end{array}\right.\right.$.

Bước 3:
Do số tiền cho mỗi loại kẹo bằng nhau nên số tiền cho mỗi loại sẽ là $\dfrac{1,200,000}{2}=600,000$.
Vậy giá tiền mỗi kg kẹo loại $A$ và $B$ lần lượt là $\dfrac{600,000}{6}=100,000$ và $\dfrac{600,000}{12}=50,000$

Vậy có đáp án D là thỏa mãn bài toán.