Thể tích của khối chóp
Kỳ thi ĐGNL ĐHQG Hồ Chí Minh
Cho khối chóp có thể tích \(V\), diện tích đáy là \(S\) và chiều cao \(h\). Chọn công thức đúng:
Công thức tính thể tích khối chóp \(V = \dfrac{1}{3}Sh\).
Phép vị tự tỉ số \(k > 0\) biến khối chóp có thể tích \(V\) thành khối chóp có thể tích \(V'\). Khi đó:
Phép vị tự tỉ số \(k > 0\) biến khối chóp có thể tích \(V\) thành khối chóp có thể tích \(V'\). Khi đó \(\dfrac{{V'}}{V} = {k^3}\).
Cho khối chóp tam giác \(S.ABC\), trên các cạnh \(SA,SB,SC\) lần lượt lấy các điểm \(A',B',C'\). Khi đó:
Nếu \(A',B',C'\) là ba điểm lần lượt nằm trên các cạnh \(SA,SB,SC\) của hình chóp tam giác \(S.ABC\). Khi đó:
\(\dfrac{{{V_{S.A'B'C'}}}}{{{V_{S.ABC}}}} = \dfrac{{SA'}}{{SA}}.\dfrac{{SB'}}{{SB}}.\dfrac{{SC'}}{{SC}}\)
Đáy của hình chóp $S.ABCD$ là một hình vuông cạnh \(a\). Cạnh bên \(SA\) vuông góc với mặt đáy và có độ dài là \(a\). Thể tích khối tứ diện \(S.BCD\) bằng:
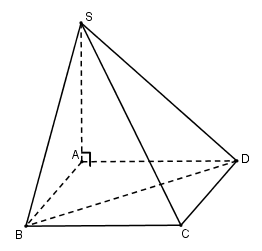
Ta có: \({S_{\Delta BCD}} = \dfrac{1}{2}{S_{ABCD}} = \dfrac{1}{2}{a^2}\)
\({V_{S.BCD}} = \dfrac{1}{3}SA.{S_{BCD}} = \dfrac{1}{3}a.\dfrac{1}{2}{a^2} = \dfrac{{{a^3}}}{6}\)
Cho hình chóp \(S.ABCD\) có \(ABCD\) là hình thang vuông tại \(A\) và \(D\) thỏa mãn \(SA \bot \left( {ABCD} \right)\) và \(AB = 2AD = 2CD = 2a = \sqrt 2 SA\). Thể tích khối chóp \(S.BCD\) là:
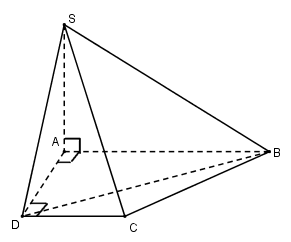
Ta có: \({S_{ABCD}} = \dfrac{1}{2}\left( {AB + CD} \right).AD = \dfrac{1}{2}\left( {2a + a} \right)a = \dfrac{{3{a^2}}}{2}\)
\({S_{\Delta ABD}} = \dfrac{1}{2}AD.AB = \dfrac{1}{2}a.2a = {a^2}\)
\( \Rightarrow {S_{BCD}} = {S_{ABCD}} - {S_{ABD}} = \dfrac{{3{a^2}}}{2} - {a^2} = \dfrac{{{a^2}}}{2}\)
\(SA = \dfrac{{2a}}{{\sqrt 2 }} = a\sqrt 2 \)
\( \Rightarrow {V_{S.BCD}} = \dfrac{1}{3}SA.{S_{BCD}} = \dfrac{1}{3}a\sqrt 2 .\dfrac{{{a^2}}}{2} = \dfrac{{{a^3}\sqrt 2 }}{6}\)
Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\). Biết \(AC = a\sqrt 2 \), cạnh \(SC\) tạo với đáy một góc \({60^0}\) và diện tích tứ giác \(ABCD\) là \(\dfrac{{3{a^2}}}{2}\). Gọi \(H\) là hình chiếu của \(A\) trên cạnh \(SC\). Tính thể tích khối chóp \(H.ABCD\).
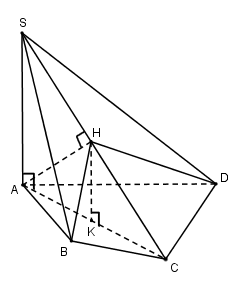
Ta có: \(SA \bot \left( {ABCD} \right) \Rightarrow AC\)là hình chiếu của $SC$ trên \(\left( {ABCD} \right) \Rightarrow \widehat {\left( {SC;\left( {ABCD} \right)} \right)} = \widehat {\left( {SC;AC} \right)} = {60^0}\)
\(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AC \Rightarrow \Delta SAC\) vuông tại $A$ và $\widehat {SCA} = {60^0}$
Xét tam giác vuông $SAC$ có: \(SA = AC.\tan 60 = a\sqrt 2 .\sqrt 3 = a\sqrt 6 ;\,SC = \dfrac{{AC}}{{{\rm{cos60}}}} = \dfrac{{a\sqrt 2 }}{{\dfrac{1}{2}}} = 2a\sqrt 2 \)
Áp dụng hệ thức lượng trong tam giác vuông $SAC$ có: \(A{C^2} = HC.SC \Rightarrow \dfrac{{HC}}{{SC}} = \dfrac{{A{C^2}}}{{S{C^2}}} = \dfrac{{2{a^2}}}{{8{a^2}}} = \dfrac{1}{4}\)
Trong $\left( {SAC} \right)$ kẻ \(HK//SA \Rightarrow HK \bot \left( {ABCD} \right)\)
Ta có: \(\dfrac{{HK}}{{SA}} = \dfrac{{HC}}{{SC}} = \dfrac{1}{4} \Rightarrow HK = \dfrac{1}{4}SA = \dfrac{{a\sqrt 6 }}{4}\)
Vậy \({V_{H.ABCD}} = \dfrac{1}{3}HK.{S_{ABCD}} = \dfrac{1}{3}.\dfrac{{a\sqrt 6 }}{4}.\dfrac{{3{a^2}}}{2} = \dfrac{{{a^3}\sqrt 6 }}{8}\)
Cho hình chóp \(S.ABC\) có \(SA \bot SB,SB \bot SC,SA \bot SC;SA = 2a,SB = b,SC = c\). Thể tích khối chóp là:
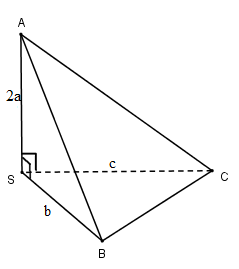
Ta có: \(\left. \begin{array}{l}SA \bot SB\\SA \bot SC\\SB \bot SC\end{array} \right\} \Rightarrow S.ABC\) là tứ diện vuông.
\( \Rightarrow {V_{S.ABC}} = \dfrac{1}{6}SA.SB.SC = \dfrac{1}{6}.2a.b.c = \dfrac{1}{3}abc\).
Cho hình chóp \(S.ABC\) có đáy \(ABC\) vuông tại \(A\) và \(SB\) vuông góc với đáy. Biết \(SB = a,SC\) hợp với \(\left( {SAB} \right)\) một góc \({30^0}\) và \(\left( {SAC} \right)\) hợp với đáy \(\left( {ABC} \right)\) một góc \({60^0}\). Thể tích khối chóp là:
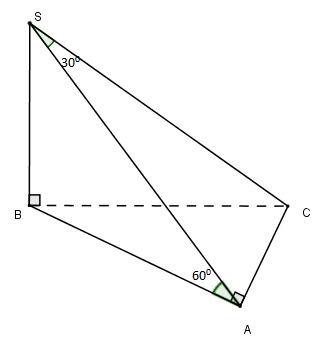
Ta có:
\(\left. \begin{array}{l}AC \bot AB\\AC \bot SB\,\,\left( {SB \bot \left( {ABC} \right)} \right)\end{array} \right\} \Rightarrow AC \bot \left( {SAB} \right) \Rightarrow AC \bot SA\)
\( \Rightarrow SA\) là hình chiếu vuông góc của $SC$ trên $\left( {SAB} \right) \Rightarrow \widehat {\left( {SC;\left( {SAB} \right)} \right)} = \widehat {\left( {SC;SA} \right)} = \widehat {CSA} = {30^0}$
\(\left. \begin{array}{l}\left( {SAC} \right) \cap \left( {ABC} \right) = AC\\\left( {SAC} \right) \supset SA \bot AC\\\left( {ABC} \right) \supset AB \bot AC\end{array} \right\} \Rightarrow \widehat {\left( {\left( {SAC} \right);\left( {ABC} \right)} \right)} = \widehat {\left( {SA;AB} \right)} = \widehat {SAB} = {60^0}\)
\(SB \bot \left( {ABC} \right) \Rightarrow SB \bot AB \Rightarrow \Delta SAB\) vuông tại $B$
\( \Rightarrow AB = SB.\cot {60^0} = a.\dfrac{1}{{\sqrt 3 }} = \dfrac{{a\sqrt 3 }}{3}\)
\( \Rightarrow SA = \sqrt {S{B^2} + A{B^2}} = \sqrt {{a^2} + \dfrac{{{a^2}}}{3}} = \dfrac{{2a}}{{\sqrt 3 }}\)
Xét tam giác vuông $SAC$ ta có: \(AC = SA.\tan {30^0} = \dfrac{{2a}}{{\sqrt 3 }}.\dfrac{1}{{\sqrt 3 }} = \dfrac{{2a}}{3}\)
\({S_{ABC}} = \dfrac{1}{2}AB.AC = \dfrac{1}{2}\dfrac{{a\sqrt 3 }}{3}.\dfrac{{2a}}{3} = \dfrac{{{a^2}\sqrt 3 }}{9}\)
\({V_{S.ABC}} = \dfrac{1}{3}SB.{S_{ABC}} = \dfrac{1}{3}.a.\dfrac{{{a^2}\sqrt 3 }}{9} = \dfrac{{{a^3}\sqrt 3 }}{{27}}\)
Cho tứ diện \(ABCD\) có các cạnh \(AB,AC,AD\) đôi một vuông góc với nhau, \(AB = 6a,AC = 7a,AD = 4a\). Gọi \(M,N,P\) lần lượt là trung điểm của các cạnh \(BC,CD,DB\). Thể tích \(V\) của tứ diện \(AMNP\) là:
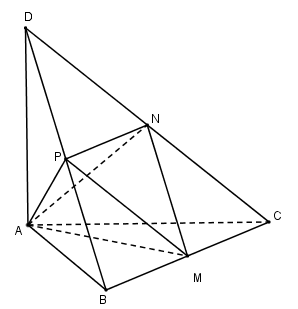
Ta có:
\(ABCD\) là tứ diện vuông tại \(A\) nên \({V_{ABCD}} = \dfrac{1}{6}AB.AC.AD = \dfrac{1}{6}.6a.7a.4a = 28{a^3}\).
Áp dụng công thức tính tỉ lệ thể tích các khối tứ diện ta có:
\(\dfrac{{{V_{DAPN}}}}{{{V_{DABC}}}} = \dfrac{{DA}}{{DA}}.\dfrac{{DP}}{{DB}}.\dfrac{{DN}}{{DC}} = \dfrac{1}{1}.\dfrac{1}{2}.\dfrac{1}{2} = \dfrac{1}{4} \Rightarrow {V_{DAPN}} = \dfrac{1}{4}{V_{DABC}} = \dfrac{1}{4}.28{a^3} = 7{a^3}\)
\(\dfrac{{{V_{BAPM}}}}{{{V_{BADC}}}} = \dfrac{{BA}}{{BA}}.\dfrac{{BP}}{{BD}}.\dfrac{{BM}}{{BC}} = \dfrac{1}{1}.\dfrac{1}{2}.\dfrac{1}{2} = \dfrac{1}{4} \Rightarrow {V_{BAPM}} = \dfrac{1}{4}{V_{BADC}} = \dfrac{1}{4}.28{a^3} = 7{a^3}\)
\(\dfrac{{{V_{CAMN}}}}{{{V_{CABD}}}} = \dfrac{{CA}}{{CA}}.\dfrac{{CM}}{{CB}}.\dfrac{{CN}}{{CD}} = \dfrac{1}{1}.\dfrac{1}{2}.\dfrac{1}{2} = \dfrac{1}{4} \Rightarrow {V_{CAMN}} = \dfrac{1}{4}{V_{CABD}} = \dfrac{1}{4}.28{a^3} = 7{a^3}\)
Do đó \({V_{AMNP}} = {V_{ABCD}} - {V_{DAPN}} - {V_{BAPM}} - {V_{CAMN}} = 28{a^3} - 7{a^3} - 7{a^3} - 7{a^3} = 7{a^3}\)
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\). Mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SAD} \right)\) cùng vuông góc với mặt phẳng \(\left( {ABCD} \right)\). Đường thẳng \(SC\) tạo với đáy góc \({45^0}\). Gọi \(M,N\) lần lượt là trung điểm của \(AB\) và \(AD\). Thể tích của khối chóp \(S.MCDN\) là:
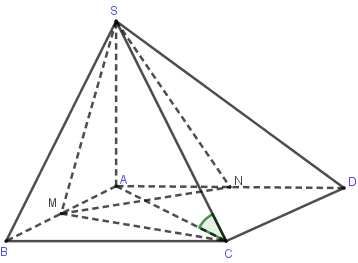
\(\left. \begin{array}{l}\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAD} \right) \bot \left( {ABCD} \right)\\\left( {SAB} \right) \cap \left( {SAD} \right) = SA\end{array} \right\} \Rightarrow SA \bot \left( {ABCD} \right)\)
\( \Rightarrow AC\) là hình chiếu vuông góc của $SC$ trên \(\left( {ABCD} \right) \Rightarrow \widehat {\left( {SC;\left( {ABCD} \right)} \right)} = \widehat {\left( {SC;AC} \right)} = \widehat {SCA} = {45^0}\)
(vì \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AC \Rightarrow \Delta SAC\) vuông tại \(A \Rightarrow \widehat {SCA} < {90^o}\))
\( \Rightarrow SA = AC = a\sqrt 2 \)
\(\begin{array}{l}{S_{ABCD}} = {a^2}\\{S_{AMN}} = \dfrac{1}{2}AM.AN = \dfrac{1}{2}\dfrac{a}{2}\dfrac{a}{2} = \dfrac{{{a^2}}}{8}\\{S_{BCM}} = \dfrac{1}{2}BM.BC = \dfrac{1}{2}\dfrac{a}{2}.a = \dfrac{{{a^2}}}{4}\\ \Rightarrow {S_{MCDN}} = {S_{ABCD}} - {S_{AMN}} - {S_{BCM}} = {a^2} - \dfrac{{{a^2}}}{8} - \dfrac{{{a^2}}}{4} = \dfrac{{5{a^2}}}{8}\\ \Rightarrow {V_{S.MCDN}} = \dfrac{1}{3}SA.{S_{MCDN}} = \dfrac{1}{3}a\sqrt 2 .\dfrac{{5{a^2}}}{8} = \dfrac{{5{a^3}\sqrt 2 }}{{24}}\end{array}\)
Cho khối lăng trụ tam giác đều \(ABC.{A_1}{B_1}{C_1}\) có tất cả các cạnh bằng \(a\). Gọi \(M\) là trung điểm của \(A{A_1}\). Thể tích khối chóp \(M.BC{A_1}\) là:
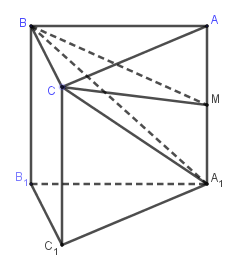
$\Delta ABC$ là tam giác đều cạnh $a$ nên có diện tích ${S_{ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}$
Ta có $AM = \dfrac{{A{A_1}}}{2} = \dfrac{a}{2}$
Hai tứ diện $MABC$ và $M{A_1}BC$ có chung đỉnh $C$, diện tích hai đáy $MAB$ và $M{A_1}B$ bằng nhau nên có thể tích bằng nhau, suy ra
${V_{M.BC{A_1}}} = {V_{M.ABC}} = \dfrac{1}{3}AM.{S_{ABC}} = \dfrac{{{a^3}\sqrt 3 }}{{24}}$
Cho hình chóp đều $S.ABCD$ có cạnh bên và cạnh đáy bằng $a$. Thể tích của khối chóp $S.ABCD$ là:
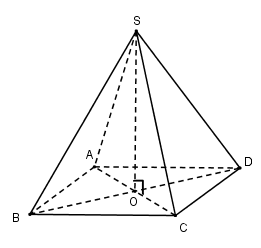
Gọi \(O = AC \cap BD\)
Vì chóp $S.ABCD$ đều nên \(SO \bot \left( {ABCD} \right)\)
Ta có: \(AC = BD = a\sqrt 2 \Rightarrow OA = \dfrac{1}{2}AC = \dfrac{{a\sqrt 2 }}{2}\)
\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OA \Rightarrow \Delta SOA\) vuông tại O \( \Rightarrow SO = \sqrt {S{A^2} - O{A^2}} = \sqrt {{a^2} - \dfrac{{{a^2}}}{2}} = \dfrac{{a\sqrt 2 }}{2}\)
Vậy \({V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}} = \dfrac{1}{3}\dfrac{{a\sqrt 2 }}{2}{a^2} = \dfrac{{{a^3}\sqrt 2 }}{6}\)
Cho hình chóp tam giác đều $S.ABC$ có cạnh đáy bằng $a$, góc giữa cạnh bên và mặt đáy bằng \({60^0}\). Tính thể tích khối chóp $S.ABC$?
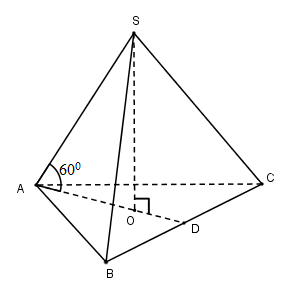
Gọi O là trọng tâm tam giác đều ABC
Vì chóp S.ABC đều nên \(SO \bot \left( {ABC} \right)\)
\( \Rightarrow OA\) là hình chiếu vuông góc của SA lên \(\left( {ABC} \right)\)\( \Rightarrow \widehat {\left( {SA;\left( {ABC} \right)} \right)} = \widehat {\left( {SA;OA} \right)} = \widehat {SAO} = {60^0}\)
\(SO \bot \left( {ABC} \right) \Rightarrow SO \bot OA \Rightarrow \Delta SAO\) vuông tại O
Gọi D là trung điểm của BC ta có: \(AD = \dfrac{{a\sqrt 3 }}{2}\)\( \Rightarrow AO = \dfrac{2}{3}AD = \dfrac{2}{3}\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\)
\( \Rightarrow SO = AO.\tan 60 = \dfrac{{a\sqrt 3 }}{3}.\sqrt 3 = a\)
Vì tam giác ABC đều nên \({S_{\Delta ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\)
Vậy \({V_{S.ABC}} = \dfrac{1}{3}SO.{S_{\Delta ABC}} = \dfrac{1}{3}a\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 3 }}{{12}}\)
Cho hình chóp đều $S.ABCD$ có diện tích đáy là \(16c{m^2}\), diện tích một mặt bên là \(8\sqrt 3 c{m^2}\). Thể tích khối chóp $S.ABCD$ là:
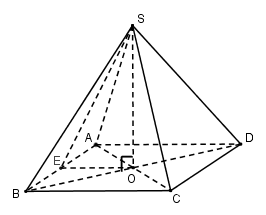
Gọi \(O = AC \cap BD\). Vì chóp $S.ABCD$ đều nên \(SO \bot \left( {ABCD} \right)\)
Vì chóp $S.ABCD$ đều nên $ABCD$ là hình vuông \( \Rightarrow {S_{ABCD}} = A{B^2} = 16 \Rightarrow AB = 4\left( {cm} \right) = AD\)
Gọi $E$ là trung điểm của AB\( \Rightarrow OE\) là đường trung bình của tam giác ABD\( \Rightarrow OE//AD \Rightarrow OE \bot AB\) và \(OE = \dfrac{1}{2}AD = \dfrac{1}{2}.4 = 2\left( {cm} \right)\)
\(\left. \begin{array}{l}OE \bot AB\\SO \bot AB\,\,\left( {SO \bot \left( {ABCD} \right)} \right)\end{array} \right\} \Rightarrow AB \bot \left( {SOE} \right) \Rightarrow AB \bot SE\)
\( \Rightarrow {S_{\Delta SAB}} = \dfrac{1}{2}SE.AB = 8\sqrt 3 \Rightarrow SE = \dfrac{{16\sqrt 3 }}{{AB}} = \dfrac{{16\sqrt 3 }}{4} = 4\sqrt 3 \left( {cm} \right)\)
\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OE \Rightarrow \Delta SOE\) vuông tại O\( \Rightarrow SO = \sqrt {S{E^2} - O{E^2}} = \sqrt {48 - 4} = \sqrt {44} = 2\sqrt {11} \left( {cm} \right)\)
Vậy \({V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}} = \dfrac{1}{3}.2\sqrt {11} .16 = \dfrac{{32\sqrt {11} }}{3}\left( {c{m^3}} \right)\)
Cho hình chóp tam giác đều $S.ABC$ có cạnh đáy bằng $a$ và mặt bên hợp với đáy một góc \({60^0}\). Thể tích khối chóp $S.ABC$ là:
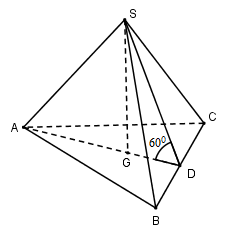
Bước 1:
Gọi $G$ là trọng tâm tam giác $ABC$. Vì chóp $S.ABC$ đều nên \(SG \bot \left( {ABC} \right)\)
Gọi $D$ là trung điểm của $BC$ ta có: \(AD \bot BC\)
Ta có: \(\left. \begin{array}{l}BC \bot AD\\BC \bot SG\,\,\left( {SG \bot \left( {ABC} \right)} \right)\end{array} \right\} \Rightarrow BC \bot \left( {SAD} \right) \Rightarrow BC \bot SD\)
\(\left. \begin{array}{l}\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\\left( {SBC} \right) \supset SD \bot BC\\\left( {ABC} \right) \supset AD \bot BC\end{array} \right\} \Rightarrow \widehat {\left( {\left( {SBC} \right);\left( {ABC} \right)} \right)} = \widehat {\left( {SD;AD} \right)} = \widehat {SDA} = {60^0}\)
Bước 2:
Vì tam giác $ABC$ đều cạnh $a$ nên \(AD = \dfrac{{a\sqrt 3 }}{2} \Rightarrow DG = \dfrac{1}{3}AD = \dfrac{{a\sqrt 3 }}{6}\)
\(SG \bot \left( {ABC} \right) \Rightarrow SG \bot AD \Rightarrow \Delta SGD\) vuông tại $G$
\( \Rightarrow SG = GD.\tan 60 = \dfrac{{a\sqrt 3 }}{6}.\sqrt 3 = \dfrac{a}{2}\)
Bước 3:
Tam giác $ABC$ đều \( \Rightarrow {S_{\Delta ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\)
Bước 4:
\( \Rightarrow {V_{S.ABC}} = \dfrac{1}{3}SG.{S_{\Delta ABC}} = \dfrac{1}{3}.\dfrac{a}{2}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 3 }}{{24}}\)
Cho hình chóp tứ giác đều $S.ABCD$ có chiều cao $h$, góc ở đỉnh của mặt bên bằng \({60^0}\). Thể tích hình chóp là:
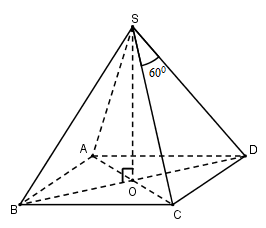
Gọi \(O = AC \cap BD\).
Vì chóp $S.ABCD$ đều nên \(SO \bot \left( {ABCD} \right)\)
Đặt \(SA = SB = SC = SD = a\)
Tam giác $SCD$ có:\(SC = SD;\widehat {CSD} = {60^0} \Rightarrow \Delta SCD\) đều\( \Rightarrow CD = SC = SD = a\)
\( \Rightarrow \) Hình vuông $ABCD$ cạnh \(a \Rightarrow AC = BD = a\sqrt 2 \Rightarrow OC = \dfrac{1}{2}AC = \dfrac{{a\sqrt 2 }}{2}\)
\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OC \Rightarrow \Delta SOC\) vuông tại $O$
\( \Rightarrow SO = \sqrt {S{C^2} - O{C^2}} \Rightarrow h = \sqrt {{a^2} - \dfrac{{{a^2}}}{2}} = \dfrac{{a\sqrt 2 }}{2} \Rightarrow a = h\sqrt 2 \)
\( \Rightarrow {S_{ABCD}} = {a^2} = {\left( {h\sqrt 2 } \right)^2} = 2{h^2}\)
Vậy \({V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}} = \dfrac{1}{3}h.2{h^2} = \dfrac{{2{h^3}}}{3}\)
Thể tích khối bát diện đều cạnh \(a\) bằng:
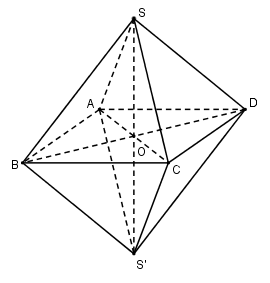
Thể tích khối bát diện đều \(V = 2{V_{S.ABCD}}\)
Gọi \(O = AC \cap BD \Rightarrow SO \bot \left( {ABCD} \right)\)
Vì ABCD là hình vuông nên \(AC = BD = a\sqrt 2 \Rightarrow OA = \dfrac{1}{2}AC = \dfrac{{a\sqrt 2 }}{2}\)
\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OA \Rightarrow \Delta SOA\) vuông tại O\( \Rightarrow SO = \sqrt {S{A^2} - O{A^2}} = \sqrt {{a^2} - \dfrac{{{a^2}}}{2}} = \dfrac{{a\sqrt 2 }}{2}\)
\( \Rightarrow {V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}} = \dfrac{1}{3}\dfrac{{a\sqrt 2 }}{2}.{a^2} = \dfrac{{{a^3}\sqrt 2 }}{6}\)
\( \Rightarrow V = 2\dfrac{{{a^3}\sqrt 2 }}{6} = \dfrac{{{a^3}\sqrt 2 }}{3}\)
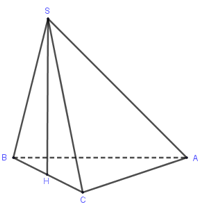
Cho hình chóp \(S.ABC\) đáy \(ABC\) là tam giác vuông tại \(A,AB = a,AC = a\sqrt 3 \). Tam giác $SBC$ đều nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp $S.ABC$
Trong $mp(SBC)$ kẻ \(SH \bot BC\left( {H \in BC} \right) \Rightarrow SH \bot \left( {ABC} \right),H\) là trung điểm \(BC\)
Xét tam giác vuông $ABC$ có \(BC = \sqrt {{a^2} + 3{a^2}} = 2a \Rightarrow \Delta SBC\) đều cạnh $2a$
\( \Rightarrow SH = \dfrac{{2a\sqrt 3 }}{2} = a\sqrt 3 \Rightarrow {V_{S.ABC}} = \dfrac{1}{3}SH.{S_{\Delta ABC}} = \dfrac{1}{6}SH.AB.AC = \dfrac{1}{2}{a^3}\)
Cho hình chóp đều $S.ABCD$ có cạnh đáy bằng $2a$. Khoảng cách giữa hai đường thẳng $SA$ và $CD$ bằng \(a\sqrt 3 \). Thể tích khối chóp $S.ABCD$ là:
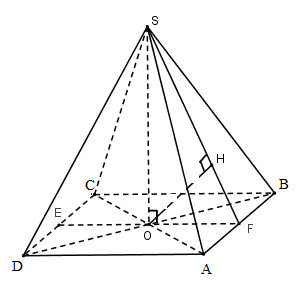
Gọi \(O = AC \cap BD\). Vì chóp $S.ABCD$ đều nên \(SO \bot \left( {ABCD} \right)\)
Gọi $E$ và $F$ lần lượt là trung điểm của $CD$ và $AB$
Ta có:
\(\begin{array}{l}AB//CD \Rightarrow SA \subset \left( {SAB} \right)//CD\\ \Rightarrow d\left( {CD;SA} \right) = d\left( {CD;\left( {SAB} \right)} \right) = d\left( {E;\left( {SAB} \right)} \right) = 2d\left( {O;\left( {SAB} \right)} \right) = a\sqrt 3 \\ \Rightarrow d\left( {O;\left( {SAB} \right)} \right) = \dfrac{{a\sqrt 3 }}{2}\end{array}\)
Ta có:
\(\left. \begin{array}{l}OF \bot AB\\SO \bot AB\,\,\left( {SO \bot \left( {ABCD} \right)} \right)\end{array} \right\} \Rightarrow AB \bot \left( {SOF} \right)\)
Trong $\left( {SOF} \right)$ kẻ \(OH \bot SF\,\,\left( 1 \right)\)
Vì \(AB \bot \left( {SOF} \right) \Rightarrow AB \bot OH\,\,\left( 2 \right)\)
Từ (1) và (2) suy ra \(OH \bot \left( {SAB} \right) \Rightarrow d\left( {O;\left( {SAB} \right)} \right) = OH = \dfrac{{a\sqrt 3 }}{2}\)
Xét tam giác vuông SOF có: \(\dfrac{1}{{O{H^2}}} = \dfrac{1}{{S{O^2}}} + \dfrac{1}{{O{F^2}}}\)
\( \Rightarrow \dfrac{1}{{S{O^2}}} = \dfrac{1}{{O{H^2}}} - \dfrac{1}{{O{F^2}}} = \dfrac{4}{{3{a^2}}} - \dfrac{1}{{{a^2}}} = \dfrac{1}{{3{a^2}}} \Rightarrow SO = a\sqrt 3 \)
Vậy \({V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}} = \dfrac{1}{3}a\sqrt 3 .4{a^2} = \dfrac{{4{a^3}\sqrt 3 }}{3}\)
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\), \(SA\) vuông góc với mặt phẳng đáy \(\left( {ABCD} \right)\) và \(SA = a\). Điểm $M$ thuộc cạnh $SA$ sao cho \(\dfrac{{SM}}{{SA}} = k\). Xác định $k$ sao cho mặt phẳng \(\left( {BMC} \right)\) chia khối chóp \(S.ABCD\) thành hai phần có thể tích bằng nhau.
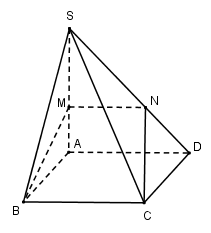
Vì $BC//AD$ nên mặt phẳng $\left( {BMC} \right)$ cắt $\left( {SAD} \right)$ theo đoạn thẳng $MN//AD\left( {N \in SD} \right)$
Vì \(MN//AD \Rightarrow \dfrac{{SM}}{{SA}} = \dfrac{{SN}}{{SD}} = k\)
$\begin{array}{l}\dfrac{{{V_{S.MBC}}}}{{{V_{S.ABC}}}} = \dfrac{{SM}}{{SA}} = k \Rightarrow {V_{S.MBC}} = k.{V_{S.ABC}} = \dfrac{k}{2}.{V_{S.ABCD}}\\\dfrac{{{V_{S.MNC}}}}{{{V_{S.ADC}}}} = \dfrac{{SM}}{{SA}}.\dfrac{{SN}}{{SD}} = {k^2} \Rightarrow {V_{S.MNC}} = {k^2}.{V_{S.ADC}} = \dfrac{{{k^2}}}{2}.{V_{S.ABCD}}\\ \Rightarrow {V_{S.MBCN}} = {V_{S.MBC}} + {V_{S.MNC}} = \left( {\dfrac{k}{2} + \dfrac{{{k^2}}}{2}} \right){V_{S.ABCD}}\end{array}$
Để mặt phẳng $\left( {BMNC} \right)$ chia hình chóp thành 2 phần có thể tích bằng nhau thì $\dfrac{k}{2} + \dfrac{{{k^2}}}{2} = \dfrac{1}{2} \Leftrightarrow {k^2} + k - 1 = 0 \Leftrightarrow k = \dfrac{{ - 1 + \sqrt 5 }}{2}$ do $k > 0$.

