Phương trình logarit và một số phương pháp giải

Phương trình tương đương với:

$3 - x = {\left( {\dfrac{1}{2}} \right)^2} \Leftrightarrow x = \dfrac{{11}}{4}$

Vậy $x = \dfrac{{11}}{4}$.

Điều kiện: $\left\{ \begin{array}{l}{x^2} - 1 > 0\\2x > 0\end{array} \right. \Leftrightarrow x > 1$.

Với điều kiện này thì phương trình đã cho tương đương với

${x^2} - 1 = 2x \Leftrightarrow {x^2} - 2x - 1 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1 + \sqrt 2 {\rm{ }}\left( {TM} \right)\\x = 1 - \sqrt 2 {\rm{ }}\left( L \right)\end{array} \right.$.

Vậy tập nghiệm của phương trình đã cho là $S = \left\{ {1 + \sqrt 2 } \right\}$

${\log _3}(x + 2) + {\log _9}{(x + 2)^2} = \dfrac{5}{4}$ (*)

Đkxđ: $x >  - 2$

$(*) \Leftrightarrow {\log _3}(x + 2) + {\log _3}(x + 2) = \dfrac{5}{4} \Leftrightarrow {\log _3}(x + 2) = \dfrac{5}{8}$

$\Leftrightarrow x + 2 = {3^{\dfrac{5}{8}}} \Leftrightarrow x = \sqrt[8]{{{3^5}}} - 2(tm)$

${\log _3}\left( {2x - 1} \right) = 2 \Leftrightarrow 2x - 1 = {3^2} \Leftrightarrow 2x = 10 \Leftrightarrow x = 5$

Điều kiện $x \ge 1$

${\log _4}\left( {x - 1} \right) = 3 \Leftrightarrow x - 1 = {4^3} \Leftrightarrow x = 65$

Điều kiện : $x>1.$

${\log _2}\left( {x - 1} \right) + {\log _2}\left( {x + 1} \right) = 3 \Leftrightarrow {\log _2}\left( {\left( {x - 1} \right).\left( {x + 1} \right)} \right) = 3$

$\Leftrightarrow {x^2} - 1 = {2^3} \Leftrightarrow x =  \pm 3$

So sánh với điều kiện suy ra $x=3$.

Đặt ${\log _4}a = {\log _6}b = {\log _9}\left( {a + b} \right) = x \Leftrightarrow \left\{ \begin{array}{l}a = {4^x}\\b = {6^x}\\a + b = {9^x}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\dfrac{a}{b} = {\left( {\dfrac{4}{6}} \right)^x} = {\left( {\dfrac{2}{3}} \right)^x} > 0\\{4^x} + {6^x} = {9^x}(1)\end{array} \right.$

giải (1) ${4^x} + {6^x} = {9^x} \Leftrightarrow {\left( {\dfrac{2}{3}} \right)^{2x}} + {\left( {\dfrac{2}{3}} \right)^x} - 1 = 0 \Leftrightarrow \left[ \begin{array}{l}{\left( {\dfrac{2}{3}} \right)^x} = \dfrac{{ - 1 + \sqrt 5 }}{2}\\{\left( {\dfrac{2}{3}} \right)^x} = \dfrac{{ - 1 - \sqrt 5 }}{2} < 0(loai)\end{array} \right. \Rightarrow \dfrac{a}{b} = \dfrac{{ - 1 + \sqrt 5 }}{2}$

Điều kiện: $\left\{ \begin{array}{l}{x^2} - 4x + 3 > 0\\4x - 4 > 0\end{array} \right. \Leftrightarrow x > 3.$

${\log _2}\left( {{x^2} - 4x + 3} \right) = {\log _2}\left( {4x - 4} \right) \Leftrightarrow {x^2} - 4x + 3 = 4x - 4 \Leftrightarrow \left[ \begin{array}{l}x = 1(l)\\x = 7\end{array} \right.$ .

Vậy $S = \left\{ 7 \right\}$ .

Điều kiện $\left\{ {\begin{array}{*{20}{c}}{x + 1 > 0}\\{x - 3 > 0}\end{array}} \right. \Leftrightarrow x > 3$

Ta có

$\begin{array}{l}{\log _4}\left( {x + 1} \right) + {\log _4}\left( {x - 3} \right) = 3 \Leftrightarrow {\log _4}\left( {x + 1} \right)\left( {x - 3} \right) = 3\\ \Leftrightarrow \left( {x + 1} \right)\left( {x - 3} \right) = {4^3} \Leftrightarrow {x^2} - 2{\rm{x}} - 67 = 0 \Leftrightarrow x = 1 \pm 2\sqrt {17} \end{array}$

So sánh với điều kiện nghiệm của pt là $x = 1 + 2\sqrt {17}$

Điều kiện:  $x >  - \dfrac{{{3^{50}}}}{2}$

Phương trình đã cho tương đương với:

$\begin{array}{l}{\log _3}\left( {{9^{50}} + 6{x^2}} \right) = {\log _3}\left( {{9^{50}} + 4x{{.3}^{50}} + 4{x^2}} \right)\\ \Leftrightarrow 6{x^2} = 4x{.3^{50}} + 4{x^2} \Leftrightarrow {x^2} = 2x{.3^{50}} \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = {2.3^{50}}\end{array} \right.\end{array}$

Phương trình đã cho tương đương với:

$\begin{array}{l}{\log _2}({2^x} - 1)[\log _{4}2 + \log _{4}({2^x} - 1)] = 1 \Leftrightarrow {\log _2}\left( {{2^x} - 1} \right)\left[ {\dfrac{1}{2} + \dfrac{1}{2}{{\log }_2}\left( {{2^x} - 1} \right)} \right] = 1\\ \Leftrightarrow {\log _2}\left( {{2^x} - 1} \right)\left[ {1 + {{\log }_2}\left( {{2^x} - 1} \right)} \right] = 2 \Leftrightarrow \log _2^2\left( {{2^x} - 1} \right) + {\log _2}\left( {{2^x} - 1} \right) - 2 = 0\\ \Leftrightarrow \left[ \begin{array}{l}{\log _2}\left( {{2^x} - 1} \right) = 1\\{\log _2}\left( {{2^x} - 1} \right) =  - 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{2^x} - 1 = 2\\{2^x} - 1 = \dfrac{1}{4}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{2^x} = 3\\{2^x} = \dfrac{5}{4}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = {\log _2}3\\x = {\log _2}\dfrac{5}{4}\end{array} \right.\end{array}$

${\log _4}\left( {{{3.2}^x} - 1} \right) = x - 1 \Leftrightarrow {3.2^x} - 1 = {4^{x - 1}} \Leftrightarrow {4^x} - {12.2^x} + 4 = 0$

Đặt $t = {2^x}$ khi đó phương trình trở thành ${t^2} - 12t + 4 = 0$ , phương trình có hai nghiệm ${t_1},{t_2}$ thỏa mãn ${t_1}{t_2} = 4 \Leftrightarrow {2^{{x_1}}}{.2^{{x_2}}} = 4 \Leftrightarrow {2^{{x_1} + {x_2}}} = {2^2} \Leftrightarrow {x_1} + {x_2} = 2$

Điều kiện $x > 0$

Ta đặt ${\log _3}x = u;{\log _5}x = v \Rightarrow u.v = u + v$

Khi đó $x = {3^u} = {5^v}$ suy ra ${\log _3}{3^u} = {\log _3}{5^v} \Leftrightarrow u = v{\log _3}5$

$\Rightarrow uv = u + v \Leftrightarrow {v^2}{\log _3}5 = v{\log _3}5 + v$ $\Leftrightarrow {v^2}{\log _3}5 - v\left( {{{\log }_3}5 + 1} \right) = 0$ $\Leftrightarrow v\left( {v{{\log }_3}5 - {{\log }_3}5 - 1} \right) = 0$

$\Leftrightarrow \left[ \begin{array}{l}v = 0\\v{\log _3}5 - {\log _3}5 - 1 = 0\end{array} \right.$ $\Leftrightarrow \left[ \begin{array}{l}v = 0\\v = \dfrac{{{{\log }_3}5 + 1}}{{{{\log }_3}5}} = 1 + \dfrac{1}{{{{\log }_3}5}}\end{array} \right.$   

$\Rightarrow \left[ \begin{array}{l}u = 0\\u = 1 + {\log _3}5\end{array} \right. \Rightarrow \left[ \begin{array}{l}x = 1\left( {TM} \right)\\x = {3^{1 + {{\log }_3}5}} = 15\left( {TM} \right)\end{array} \right.$

Do đó phương trình có hai nghiệm ${x_1} = 1,{x_2} = 15$ và tổng hai nghiệm bằng $16$ là một số chính phương.

TXĐ : $D = R$.

$2{\log _2}\left| x \right| + {\log _2}\left| {x + 3} \right| = m \Leftrightarrow {\log _2}{\left| x \right|^2} + {\log _2}\left| {x + 3} \right| = m$

$\Leftrightarrow {\log _2}\left( {{{\left| x \right|}^2}.\left| {x + 3} \right|} \right) = m \Leftrightarrow {\left| x \right|^2}.\left| {x + 3} \right| = {2^m}$

$\Leftrightarrow {x^2}.\left| {x + 3} \right| = {2^m}$.

Xét hàm $f(x) = {x^2}.\left| {x + 3} \right|$. Ta có : $f(x) = {x^2}.\left| {x + 3} \right| = \left| {{x^3} + 3{x^2}} \right|$

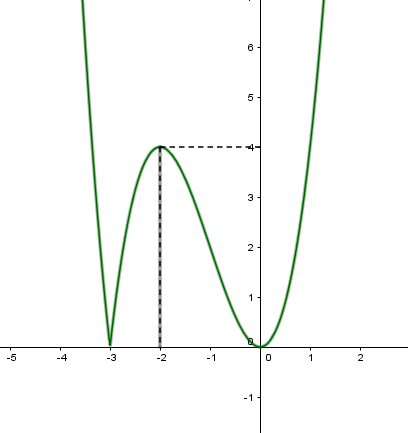
Để phương trình có 3 nghiệm phân biệt thì ${2^m} = 4 \Leftrightarrow m = 2$

$4\log _a^2x - 8{\log _b}x.{\log _a}x + 3\log _b^2x = 0$

Ta có: $\Delta ' = {(4{\log _b}x)^2} - 3.4.{\log _b}x = 4\log _b^2x > 0 \Rightarrow \left[ \begin{array}{l}{\log _a}x = \dfrac{3}{2}{\log _b}x\\{\log _a}x = \dfrac{1}{2}{\log _b}x\end{array} \right.$.

Suy ra

${\log _a}x = \dfrac{3}{2}{\log _b}x \Rightarrow {\log _a}x = {\log _{\sqrt[3]{{{b^2}}}}}x \Rightarrow a = \sqrt[3]{{{b^2}}} \Rightarrow {a^3} = {b^2}$

${\log _a}x = \dfrac{1}{2}{\log _b}x \Rightarrow {\log _a}x = {\log _{{b^2}}}x \Rightarrow a = {b^2}$

$\begin{array}{l} VT= {\log _x}2 + {\log _x}3 + {\log _x}4 + ... + {\log _x}2017 = {\log _x}(2.3.4...2017)\\ \Rightarrow {x^M} = 2017! \Rightarrow x = \sqrt[M]{{2017!}}\end{array}$

Điều kiện: $x > 0;x \ne 1$

${\log _3}x + \dfrac{1}{{{{\log }_9}x}} = 3 \Leftrightarrow {\log _3}x + \dfrac{2}{{{{\log }_3}x}} = 3 \Leftrightarrow {\left( {{{\log }_3}x} \right)^2} - 3{\log _3}x + 2 = 0$

$\Leftrightarrow \left[ \begin{array}{l}{\log _3}x = 1\\{\log _3}x = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = {3^2} = 9\end{array} \right.$

Phương trình đã cho tương đương với $\left\{ \begin{array}{l}{\log _2}\left( {\dfrac{x}{{x - 2}}} \right) = m\\x > 2\end{array} \right.$

Để phương trình đã cho có nghiệm thì đường thẳng $y = m$ cắt đồ thị hàm số $y = {\log _2}f\left( x \right)$ với $f\left( x \right) = \dfrac{x}{{x - 2}}$ trên khoảng $\left( {2; + \infty } \right)$

Có $f'\left( x \right) =  - \dfrac{2}{{{{\left( {x - 2} \right)}^2}}} < 0, ∀x > 2$ và $\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) =  + \infty ;\mathop {\lim }\limits_{x \to  + \infty } f\left( x \right) = 1$ nên ta có các tập giá trị của các hàm số là $f\left( x \right) \in \left( {1; + \infty } \right) \Rightarrow {\log _2}f\left( x \right) \in \left( {0; + \infty } \right)$

Vậy $0 < m < +∞$.

${\log _3}\left( {7 - {3^x}} \right) = 2 - x$

Điều kiện: $7 - {3^x} > 0$

$pt \Leftrightarrow 7 - {3^x} = {3^{2 - x}} \Leftrightarrow 7 - {3^x} = \dfrac{9}{{{3^x}}} \Leftrightarrow {7.3^x} - {\left( {{3^x}} \right)^2} = 9\, \Leftrightarrow {3^{2x}} - {7.3^x} + 9 = 0\,\,\left( * \right)$

Đặt $t = {3^x}\;\;\left( {t > 0} \right) \Rightarrow x = {\log _3}t$ . Thay vào phương trình (*) ta có:

$\Leftrightarrow {t^2} - 7t + 9 = 0\,\,\,\,\left( {**} \right)$

Nhận thấy (**) có: $\Delta  = 13 > 0,\;\;S = 7 > 0,\;\;P = 9 > 0 \Rightarrow$  phương trình (**) có 2 nghiệm dương phân biệt giả sử là: ${t_1};{t_2}$

Áp dụng hệ thức Vi-et cho phương trình  (**)  ta được: $\left\{ \begin{array}{l}{t_1} + {t_2} = 7\\{t_1}{t_2} = 9\end{array} \right.$

Khi đó ta có: ${x_1} + {x_2} = {\log _3}{t_1} + {\log _3}{t_2} = {\log _3}\left( {{t_1}{t_2}} \right) = {\log _3}9 = 2$

Ta có: ${\log _2}\left( {2x + 2} \right) + x - 3y = {8^y} \Leftrightarrow {\log _2}\left( {x + 1} \right) + x + 1 = {2^{3y}} + 3y$ (*)

Xét hàm số $y = f\left( x \right) = {2^x} + x$ có $f'\left( x \right) = {2^x}\ln 2 + 1 > 0\,\,\forall x \in \mathbb{R}$ $\Rightarrow$ Hàm số đồng biến trên $\mathbb{R}.$

$\Rightarrow$ Phương trình (*)$\Leftrightarrow f\left( {{{\log }_2}\left( {x + 1} \right)} \right) = f\left( {3y} \right)$$\Leftrightarrow {\log _2}\left( {x + 1} \right) = 3y$

Do $0 \le x \le 2020$ nên $0 \le {\log _2}\left( {x + 1} \right) \le {\log _2}2021 \Rightarrow 0 \le 3y \le {\log _2}2021$

                             $\Leftrightarrow 0 \le y \le \dfrac{{{{\log }_2}2021}}{3} \Rightarrow y \in \left\{ {0;1;2;3} \right\}$

Với mỗi giá trị y vừa tìm được đều tìm được đúng 1 giá trị x nguyên thỏa mãn

$\Rightarrow$ Có 4 cặp số $\left( {x;y} \right)$ nguyên thỏa mãn các điều kiện trên.