Phương trình logarit và một số phương pháp giải

$({x^2} - 4)({\log _2}x + {\log _3}x + {\log _4}x + ... + {\log _{19}}x - \log _{20}^2x) = 0(*)$

Đkxđ: $x>0$

$(*) \Leftrightarrow \left[ \begin{array}{l}x = 2(tm)\\x =  - 2(ktm)\\{\log _2}x + {\log _3}x + {\log _4}x + ... + {\log _{19}}x - \log _{20}^2x = 0(**)\end{array} \right.$

$\begin{array}{l}(**) \Leftrightarrow \dfrac{{\log {\rm{x}}}}{{\log 2}} + \dfrac{{\log {\rm{x}}}}{{\log 3}} + \dfrac{{\log {\rm{x}}}}{{\log 4}} + ... + \dfrac{{\log {\rm{x}}}}{{\log 19}} - {\left( {\dfrac{{\log {\rm{x}}}}{{\log 20}}} \right)^2} = 0\\ \Leftrightarrow \log {\rm{x}}(\dfrac{1}{{\log 2}} + \dfrac{1}{{\log 3}} + \dfrac{1}{{\log 4}} + ... + \dfrac{1}{{\log 19}} - \dfrac{{\log {\rm{x}}}}{{{{\log }^2}20}}) = 0\\ \Leftrightarrow \left[ \begin{array}{l}\log {\rm{x}} = 0\\\dfrac{1}{{\log 2}} + \dfrac{1}{{\log 3}} + \dfrac{1}{{\log 4}} + ... + \dfrac{1}{{\log 19}} - \dfrac{{\log {\rm{x}}}}{{{{\log }^2}20}} = 0\end{array} \right. \\ \Leftrightarrow \left[ \begin{array}{l}x = 1\\\dfrac{1}{{\log 2}} + \dfrac{1}{{\log 3}} + \dfrac{1}{{\log 4}} + ... + \dfrac{1}{{\log 19}} = \dfrac{{\log {\rm{x}}}}{{{{\log }^2}20}}\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 1\\(\dfrac{1}{{\log 2}} + \dfrac{1}{{\log 3}} + \dfrac{1}{{\log 4}} + ... + \dfrac{1}{{\log 19}}){\log ^2}20 = \log {\rm{x}}\end{array} \right. \\ \Leftrightarrow \left[ \begin{array}{l}x = 1(tm)\\x = {10^{(\dfrac{1}{{\log 2}} + \dfrac{1}{{\log 3}} + \dfrac{1}{{\log 4}} + ... + \dfrac{1}{{\log 19}}){{\log }^2}20}}(tm)\end{array} \right.\end{array}$ 

Phương trình (*) có $3$ nghiệm.

ĐKXĐ: \(\cos x > 0\)

Ta có: \(f\left( x \right) = {\log _2}\left( {\cos x} \right) \Rightarrow f'\left( x \right) = \dfrac{{ - \sin x}}{{\cos x.\ln 2}}\)

\(f'\left( x \right) = 0 \Leftrightarrow \)\(\dfrac{{ - \sin x}}{{\cos x.\ln 2}} = 0 \Leftrightarrow \tan x = 0 \Leftrightarrow x = k\pi ,\,k \in \mathbb{Z}\).

Với \(k\) chẵn, đặt \(k = 2m\,\,\left( {m \in \mathbb{Z}} \right)\), khi đó ta có \(x = m2\pi \,\,\left( {m \in \mathbb{Z}} \right)\).

Với \(k\) lẻ, đặt \(k = 2n + 1\,\,\left( {n \in \mathbb{Z}} \right)\), khi đó ta có \(x = \left( {2n + 1} \right)\pi  = \pi  + n2\pi \,\,\left( {n \in \mathbb{Z}} \right)\).

Kiểm tra ĐKXĐ:

\(x = m2\pi  \Rightarrow \cos x = 1 > 0\): thỏa mãn.

\(x = \pi  + k2\pi  \Rightarrow \cos x =  - 1 < 0\): loại.

Suy ra nghiệm của phương trình là \(x = m2\pi ,\,\,m \in \mathbb{Z}\).

Theo bài ra ta có: \(x \in \left( {0;2020\pi } \right) \Rightarrow 0 < m2\pi  < 2020\pi  \Leftrightarrow 0 < m < 1010 \Rightarrow \) Có 1009 giá trị nguyên của m thỏa mãn.

Vậy phương trình \(f'\left( x \right) = 0\) có 1009 nghiệm trong khoảng \(\left( {0;2020\pi } \right)\).

\(\dfrac{1}{{\ln \left( {x + 5} \right)}} + \dfrac{1}{{{3^x} - 1}} = x + a \Leftrightarrow f\left( x \right) = \dfrac{1}{{\ln \left( {x + 5} \right)}} + \dfrac{1}{{{3^x} - 1}} - x = a\,\,\left( * \right)\).

Xét hàm số \(f\left( x \right) = \dfrac{1}{{\ln \left( {x + 5} \right)}} + \dfrac{1}{{{3^x} - 1}} - x\).

ĐKXĐ: \(\left\{ \begin{array}{l}x + 5 > 0\\\ln \left( {x + 5} \right) \ne 0\\{3^x} - 1 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x >  - 5\\x + 5 \ne 1\\{3^x} \ne 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x >  - 5\\x \ne  - 4\\x \ne 0\end{array} \right.\)

\( \Rightarrow D = \left( { - 5; - 4} \right) \cup \left( { - 4;0} \right) \cup \left( {0; + \infty } \right)\).

Ta có:

$f'\left( x \right) = - \frac{1}{{\left( {x + 5} \right){{\ln }^2}\left( {x + 5} \right)}} - \frac{{{3^x}\ln 3}}{{{{\left( {{3^x} - 1} \right)}^2}}} - 1 < 0,\forall x \in D$

BBT:

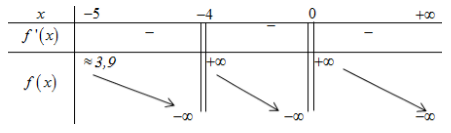
Từ BBT suy ra phương trình (*) có 2 nghiệm \( \Leftrightarrow a \ge 4\).

Kết hợp ĐK \( \Rightarrow a \in \left\{ {4;...;2018} \right\}\). Vậy có 2015 giá trị của \(a\) thỏa mãn.

Ta có: $\int\limits_0^2 {\left( {t - {{\log }_2}x} \right)dt}  = \left. {\left( {\dfrac{{{t^2}}}{2} - {{\log }_2}x.t} \right)} \right|_0^2 = 2 - 2{\log _2}x$

Phương trình: $2 - 2{\log _2}x = 2{\log _2}\dfrac{2}{x}$ có điều kiện là $x > 0$

$ \Leftrightarrow {\log _2}\dfrac{2}{x} + {\log _2}x = 1 \Leftrightarrow {\log _2}\left( {\dfrac{2}{x}.x} \right) = 1$ (luôn đúng)

Vậy tập nghiệm của phương trình là $(0; +\infty )$

Điều kiện : \(\left\{ \begin{array}{l}\cot x > 0\\\cos x > 0\end{array} \right.(1)\).

Ta có : $2{\log _3}\left( {\cot x} \right) = {\log _2}\left( {\cos x} \right) \Leftrightarrow {\log _3}{\left( {\cot x} \right)^2} = {\log _2}\left( {\cos x} \right) = t$

$ \Rightarrow \left\{ \begin{array}{l}{\left( {\cot x} \right)^2} = {3^t}\\{\cos ^2}x = {4^t}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\dfrac{{{{\cos }^2}x}}{{{{\sin }^2}x}} = {3^t}\\{\cos ^2}x = {4^t}\end{array} \right.$

\( \Rightarrow \dfrac{{{4^t}}}{{1 - {4^t}}} = {3^t} \Leftrightarrow {4^t} - {3^t} + {12^t} = 0 \Leftrightarrow {\left( {\dfrac{4}{3}} \right)^t} + {4^t} = 1\)

Đặt \(f(t) = {\left( {\dfrac{4}{3}} \right)^t} + {\left( 4 \right)^t} \Rightarrow f'(t) = {\left( {\dfrac{4}{3}} \right)^t}\ln \dfrac{4}{3} + {\left( 4 \right)^t}\ln 4 > 0\) suy ra $f(t)= 1$ có tối đa $1$ nghiệm.

Nhận thấy $t=-1$ là nghiệm của phương trình \( \Rightarrow {\log _2}\left( {\cos x} \right) =  - 1 \Rightarrow \cos x = \dfrac{1}{2} \Rightarrow x =  \pm \dfrac{\pi }{3} + k2\pi  \Rightarrow x = \dfrac{\pi }{3} + k2\pi \)( do đk (1)).

Ta có : \(0 < \dfrac{\pi }{3} + k2\pi  < 2017\pi  \Leftrightarrow  - \dfrac{1}{6} < k < \dfrac{{3025}}{3}\). Do $k$ nguyên nên $k= 0, 1, …, 1008$.

Vậy phương trình có $1009$ nghiệm.

ĐK: $x>-1;mx>0$

$\begin{array}{l}\log (m{\rm{x}}) = 2\log (x + 1) \Leftrightarrow m{\rm{x}} = {(x + 1)^2} \Leftrightarrow {x^2} + (2 - m)x + 1 = 0\\\Delta  = {m^2} - 4m + 4 - 4 = {m^2} - 4m\end{array}$

Để phương trình đã cho có nghiệm duy nhất thì có 2 TH:

TH1: Phương trình trên có nghiệm duy nhất: ${m^2} = 4m \Leftrightarrow \left[ \begin{array}{l}m = 0\\m = 4\end{array} \right..$

Tuy nhiên giá trị $m = 0$ loại do khi đó nghiệm là $x = -1$.

TH2: Phương trình trên có 2 nghiệm thỏa: ${x_1} \le  - 1 < {x_2}$

Nếu có ${x_1} =  - 1 \to 1 - (2 - m) + 1 = 0 \to m = 0$, thay lại vô lý

$\begin{array}{l}{x_1} <  - 1 < {x_2} \to ({x_1} + 1)({x_2} + 1) < 0 \Leftrightarrow {x_1}{x_2} + {x_1} + {x_2} + 1 < 0\\ \to 1 + m - 2 + 1 < 0 \Leftrightarrow m < 0.\end{array}$

Như vậy sẽ có các giá trị $-2017; - 2016; …… -1$ và $4$.

Có $2018 $ giá trị.

${\left( {{{\log }_{\frac{1}{3}}}x} \right)^2} - \left( {\sqrt 3  + 1} \right){\log _3}x + \sqrt 3  = 0$   điều kiện của phương trình là $x > 0$

$ \Leftrightarrow {\left( {{{\log }_3}x} \right)^2} - \left( {\sqrt 3  + 1} \right){\log _3}x + \sqrt 3  = 0$

Đặt $t = \log_{3}x$ , phương trình trở thành:

${t^2} - \left( {\sqrt 3  + 1} \right)t + \sqrt 3  = 0 \Rightarrow \left[ \begin{array}{l}t = 1\\t = \sqrt 3 \end{array} \right.$

$ \Rightarrow \left[ \begin{array}{l}{\log _3}x = 1\\{\log _3}x = \sqrt 3 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = {3^{\sqrt 3 }}\end{array} \right. \Rightarrow {x_1}.{x_2} = {3.3^{\sqrt 3 }} = {3^{\sqrt 3  + 1}}$

+ Cô lập  \(m : m(\ln (1 - x) - 1) = \ln x \Rightarrow m = \dfrac{{\ln x}}{{\ln (1 - x) - 1}}\) với $1 > x > 0$ .

+ Nhận xét đáp án: ta thấy \(\dfrac{{\ln x}}{{\ln (1 - x) - 1}} > 0{\rm{   }},\forall 0 < x < 1\). Loại C và D

+ Tính giới hạn của \(y =\dfrac{{\ln x}}{{\ln (1 - x) - 1}}\) khi $x$ tiến dần tới $1$ thì thấy $y$ dần tiến tới $0$ . Loại B. 

Đặt \(t = {\log _3}x\) suy ra phương trình trở thành \({t^2} - (m + 2)t + 3m - 2 = 0\)(*).

Để phương trình có hai nghiệm \({x_1};{x_2}\) thì (*) cũng có hai nghiệm \({t_1};{t_2}\) .

Phương trình (*) có 2 nghiệm phân biệt \({t_1};{t_2}\)

$ \Leftrightarrow \Delta  > 0\, \Leftrightarrow \,{\left( {m + 2} \right)^2} - 4\left( {3m - 2} \right) > 0\, \Leftrightarrow \left[ \begin{array}{l}m > 6\\m < 2\end{array} \right.$.

Ta có: $\left\{ \begin{array}{l}{x_1} = {3^{{t_1}}}\\{x_2} = {3^{{t_2}}}\end{array} \right. \Rightarrow {x_1}.{x_2} = {3^{{t_1} + {t_2}}} = 9 \Leftrightarrow {t_1} + {t_2} = 2.$

Theo hệ thức Vi-ét ta có: \({t_1} + {t_2} = m + 2\)

\( \Rightarrow m + 2 = 2 \Leftrightarrow m = 0\).

Suy ra \(m \in \left( { - 1;1} \right)\)

Đặt ${x^2} - \sqrt 2 x = t$ khi đó ${\log _3}|t| = {\log _5}(t + 2)(t >  - 2;t \ne 0)$

Đặt ${\log _3}|t| = {\log _5}(t + 2) = a \Rightarrow \left\{ \begin{array}{l}|t| = {3^a}\\t + 2 = {5^a}\end{array} \right. $

$\Rightarrow \left| {{5^a} - 2} \right| = {3^a} \Leftrightarrow \left[ \begin{array}{l}{5^a} - 2 =  - {3^a}\\{5^a} - 2 = {3^a}\end{array} \right. \Rightarrow \left[ \begin{array}{l}{5^a} + {3^a} = 2(1)\\{5^a} = {3^a} + 2(2)\end{array} \right.$

Xét (1): $f(a) = {5^a} + {3^a} \Rightarrow f'(a) = {5^a}\ln 5 + {3^a}\ln 3 > 0(\forall a \in R)$ nên hàm số đồng biến trên $R$

Mặt khác $f(0) = 2$ do đó phương trình $f(a) = f(0)$ có 1 nghiệm duy nhất $a = 0 \Rightarrow t = -1$

Suy ra: ${x^2} - \sqrt 2 x + 1 = 0$ (vô nghiệm)

Xét (2) $ \Leftrightarrow {\left( {\dfrac{3}{5}} \right)^a} + 2.{\left( {\dfrac{1}{5}} \right)^a} = 1$.

Đặt $g(a) = {\left( {\dfrac{3}{5}} \right)^a} + 2.{\left( {\dfrac{1}{5}} \right)^a} \Rightarrow g'(a) = {\left( {\dfrac{3}{5}} \right)^a}\ln \dfrac{3}{5} + 2.{\left( {\dfrac{1}{5}} \right)^a}\ln \dfrac{1}{5} < 0(\forall a \in R)$

Nên hàm số $g(a)$ nghịch biến trên $R$ do đó phương trình $g(a) = 1$ có tối đa 1 nghiệm.

Mà $g(a) = g(1)$ nên $ a = 1$

Suy ra $t = 3 \Rightarrow {x^2} - \sqrt 2 x - 3 = 0$ có 2 nghiệm phân biệt thỏa mãn điều kiện

Vậy phương trình đã cho có $2$ nghiệm.

Ta có:

\(\begin{array}{l}\,\,\,\,\,\,\,\log _a^2b + \log _b^2c = {\log _a}\dfrac{c}{b} - 2{\log _b}\dfrac{c}{b} - 3\\ \Leftrightarrow \log _a^2b + \log _b^2c = {\log _a}c - {\log _a}b - 2{\log _b}c - 1\\ \Leftrightarrow \log _a^2b + \log _b^2c = {\log _b}c.{\log _a}b - {\log _a}b - 2{\log _b}c - 1\,\,\left( * \right)\end{array}\)

Đặt \({\log _a}b = x \Rightarrow {\log _b}c = x - P\).

Phương trình (*) \( \Leftrightarrow {x^2} + {\left( {x - P} \right)^2} = \left( {x - P} \right)x - x - 2\left( {x - P} \right) - 1\)

\(\begin{array}{l} \Leftrightarrow 2{x^2} - 2Px + {P^2} = {x^2} - Px - 3x + 2P - 1\\ \Leftrightarrow {x^2} - \left( {P - 3} \right)x + {P^2} - 2P + 1 = 0\,\,\,\left( {**} \right)\end{array}\)

Ta có: \(\Delta  = {\left( {P - 3} \right)^2} - 4\left( {{P^2} - 2P + 1} \right) =  - 3{P^2} + 2P + 5\)

Phương trình (**) có nghiệm \( \Leftrightarrow \Delta  \ge 0 \Leftrightarrow  - 3{P^2} + 2P + 5 \ge 0 \Leftrightarrow  - 1 \le P \le \dfrac{5}{3}\,\, \Rightarrow \left\{ \begin{array}{l}m =  - 1\\M = \dfrac{5}{3}\end{array} \right.\).

Vậy \(S = m - 3M =  - 1 - 3.\dfrac{5}{3} =  - 6\).

Ta có:

\(\begin{array}{l}\,\,\,\,\,\,\log _{\sqrt a }^2b + {\log _b}c.{\log _b}\left( {\dfrac{{{c^2}}}{b}} \right) + 9{\log _a}c = 4{\log _a}b\\ \Leftrightarrow 4\log _a^2b + {\log _b}c.\left( {2{{\log }_b}c - 1} \right) + 9{\log _a}c = 4{\log _a}b\\ \Leftrightarrow 4\log _a^2b + 2\log _b^2c - {\log _b}c + 9{\log _a}b.{\log _b}c = 4{\log _a}b\,\,\left( * \right)\end{array}\)

Đặt \(x = {\log _a}b,\,\,y = {\log _b}c\) ta có: \(\left\{ \begin{array}{l}x = {\log _a}b > {\log _a}1 = 0\\y = {\log _b}c > {\log _b}1 = 0\end{array} \right.\,\,\left( {do\,\,a,b,c > 1} \right)\).

Khi đó phương trình (*) trở thành:

\(\begin{array}{l}\,\,\,\,\,\,4{x^2} + 2{y^2} - y + 9xy = 4x\\ \Leftrightarrow 4{x^2} + xy + 8xy + 2{y^2} - y - 4x = 0\\ \Leftrightarrow x\left( {4x + y} \right) + 2y\left( {4x + y} \right) - \left( {4x + y} \right) = 0\\ \Leftrightarrow \left( {4x + y} \right)\left( {x + 2y - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}4x + y = 0\\x + 2y - 1 = 0\end{array} \right.\end{array}\)

TH1: \(y =  - 4x\) loại do \(x,\,\,y > 0\).

TH2: \(x + 2y - 1 = 0 \Leftrightarrow x + 2y = 1\), khi đó ta có: \({\log _a}b + {\log _b}{c^2} = x + 2y = 1\).

Theo bài ra ta có: \(\left\{ \begin{array}{l}\log \left( {x + y} \right) = z\\\log \left( {{x^2} + {y^2}} \right) = z + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x + y = {10^z}\\{x^2} + {y^2} = {10.10^z}\end{array} \right. \Leftrightarrow {x^2} + {y^2} = 10\left( {x + y} \right)\).

Khi đó ta có:

\(\begin{array}{l}\,\,\,\,\,{x^3} + {y^3} = a{.10^{3z}} + b{.10^{2z}}\\ \Leftrightarrow \left( {x + y} \right)\left( {{x^2} + {y^2} - xy} \right) = a.{\left( {{{10}^z}} \right)^3} + b.{\left( {{{10}^z}} \right)^2}\\ \Leftrightarrow \left( {x + y} \right)\left( {{x^2} + {y^2} - xy} \right) = a.{\left( {x + y} \right)^3} + b.{\left( {x + y} \right)^2}\\ \Leftrightarrow {x^2} + {y^2} - xy = a{\left( {x + y} \right)^2} + b\left( {x + y} \right)\\ \Leftrightarrow {x^2} + {y^2} - xy = a\left( {{x^2} + 2xy + {y^2}} \right) + b.\dfrac{{{x^2} + {y^2}}}{{10}}\\ \Leftrightarrow {x^2} + {y^2} - xy = \left( {a + \dfrac{b}{{10}}} \right)\left( {{x^2} + {y^2}} \right) + 2a.xy\end{array}\)

Đồng nhất hệ số ta có \(\left\{ \begin{array}{l}1 = a + \dfrac{b}{{10}}\\ - 1 = 2a\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a =  - \dfrac{1}{2}\\b = 15\end{array} \right.\).

Vậy \(\dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}} = 4 + \dfrac{1}{{225}} = \dfrac{{901}}{{225}} \approx 4,004 \in \left( {4;5} \right)\).