Giải toán tư duy bằng phương pháp loại trừ, lựa chọn và chia trường hợp
Kỳ thi ĐGNL ĐHQG Hồ Chí Minh
Nếu đội N vô địch thì điều nào sau đây đúng?
Đội N thắng 4 trận: O, P, M, Q.
Đội R thắng 3 trận: M, N, P.
Do đó nếu đội N vô địch thì đội R phải thua 3 đội Q, O, S.
Tổng số điểm của 7 đội sau khi mùa giải kết thúc là:
Từ kết quả câu 2, ta thấy tổng số trận thắng của 7 đội là 21 trận.
Do đó tổng số điểm của 7 đội sau khi mùa giải kết thúc là: \(21.2 = 42\) (điểm).
Nếu đội O chỉ thắng 2 trận và có 3 đội cùng được 6 điểm thì đội nào vô địch?
Do đội O chỉ thắng 2 trận nên đội O thắng đội M và đội Q.
Khi đó đội O thua đội N, P, R, S.
Lúc này, ta thấy:
– Đội M thắng 3 trận: đội Q, S, P.
– Đội N thắng 4 trận: đội O, P, M, Q.
– Đội O thắng 2 trận: đội M, Q.
– Đội P thắng 3 trận: đội O, S, Q.
– Đội Q thắng 1 trận: đội R.
– Đội R thắng 4 trận: đội M, N, P, O.
– Đội S thắng 3 trận: N, Q, O.
Giả sử R thua S, khi đó ta có 3 đội thắng 4 trận là: đội N, R, S (mâu thuẫn với dữ kiện chỉ có 1 đội duy nhất là đội vô địch).
Do đó đội R phải thắng đội S.
Vì vậy đội R thắng 5 trận.
Vậy đội R là đội vô địch.
Đội M đạt được bao nhiêu điểm?
Do đội P thắng đội O và đội S; đội Q chỉ thắng được đội R.
Nên đội P thắng 3 đội: O, S, Q.
Mà đội P thua ít nhất 3 trận nên đội P thua đội M, N, R.
Khi đó đội M thắng đội: Q, S, P.
Vậy số điểm đội M đạt được là 6 điểm.
Thành tích thi của A đứng thứ mấy?
Theo giả thiết: D: Xem ra tôi thứ nhất, A thứ hai.
=> Ta xét 2 trường hợp: Hoặc D thứ nhất, hoặc A thứ hai.
TH1: Giả sử A thứ hai
=> D không thể thứ nhất.
Theo B: Tôi thứ hai, C cuối cùng.
Mà A thứ hai => B không thể thứ hai => C cuối cùng.
Theo C: Không thể như vậy, D chỉ thứ hai, tôi thứ ba.
=> D thứ hai (Mâu thuẫn với giả sử).
=> Loại.
TH2: Giả sử D thứ nhất.
=> A không thể thứ hai.
Theo C: Không thể như vậy, D chỉ thứ hai, tôi thứ ba.
=> C thứ ba.
Theo B: Tôi thứ hai, C cuối cùng.
Mà C không đứng cuối cùng => B thứ hai
=> A thứ tư.
Thành tích thi của C đứng thứ mấy?
Theo giả thiết: D: Xem ra tôi thứ nhất, A thứ hai.
=> Ta xét 2 trường hợp: Hoặc D thứ nhất, hoặc A thứ hai.
TH1: Giả sử A thứ hai
=> D không thể thứ nhất.
Theo B: Tôi thứ hai, C cuối cùng.
Mà A thứ hai => B không thể thứ hai => C cuối cùng.
Theo C: Không thể như vậy, D chỉ thứ hai, tôi thứ ba.
=> D thứ hai (Mâu thuẫn với giả sử).
=> Loại.
TH2: Giả sử D thứ nhất.
=> A không thể thứ hai.
Theo C: Không thể như vậy, D chỉ thứ hai, tôi thứ ba.
=> C thứ ba.
Thành tích thi của D đứng thứ mấy?
Theo giả thiết: D: Xem ra tôi thứ nhất, A thứ hai.
Giả sử A thứ hai
=> D không thể thứ nhất.
Theo B: Tôi thứ hai, C cuối cùng.
Mà A thứ hai => B không thể thứ hai => C cuối cùng.
Theo C: Không thể như vậy, D chỉ thứ hai, tôi thứ ba.
=> D thứ hai (Mâu thuẫn với giả sử).
=> Loại.
Vậy D thứ nhất.
Đề chính thức ĐGNL HCM 2019
Có 5 ô tô đang chạy cùng chiều trên cùng một con đường có 3 làn, xe $ {X}$ đang dẫn đầu , xe $ {N}$ chạy ngay sau xe $ {X}$, xe $ {M}$ và xe $ {P}$ chạy kề hai bên của $ {N}$, $ {Q}$ chạy sau $ {P}$ và $ {M}$ nhưng khác làn. Sau đó xe $ {M}$ giảm tốc để xe $ {N}$ và xe $ {P}$ chuyển một làn. Khi đó xe nào sẽ chạy ngay sau xe $ {X}$
Giả sử 5 ô tô chạy theo chiều từ trái sang phải.
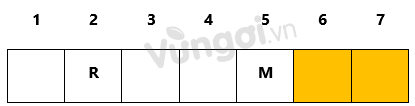
Do $ {X}$ đang dẫn đầu nên X có thể tại một trong các vị trí tô màu cam:

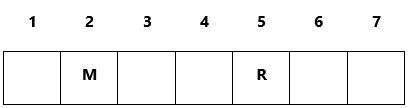
Xe $ {N}$ chạy ngay sau xe $ {X}$ nên N có thể tại một trong các vị trí tô màu vàng:

Xe $ {M}$ và xe $ {P}$ chạy kề hai bên của $ {N}$=> Xe N ở làn giữa:
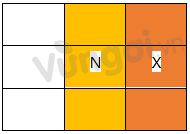
$ {Q}$ chạy sau $ {P}$ và $ {M}$ nhưng khác làn nên ta có:
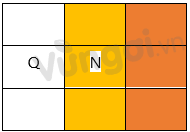
Xe $ {M}$ giảm tốc để xe $ {N}$ và xe $ {P}$ chuyển một làn
=> $P$ chuyển vào giữa và xe $N$ chuyển sang làn khác
=> $P$ chạy ngay sau xe $X$
Tiết mục M được biểu diễn ở vị trí thứ mấy để có thể xác định được thứ tự biểu diễn của Q một cách duy nhất
- Xét M ở vị trí thứ nhất:
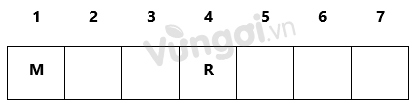
Khi đó R ở 4 và P-Q có thể ở 2-3 hoặc 5-6
=> Loại
- Xét M ở vị trí thứ 3=> R ở vị trí thứ 6
Khi đó P-Q có thể ở 1-2 hoặc 4-5=>Loại
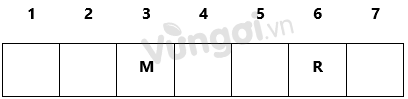
- Xét M ở vị trí thứ 5=> R ở vị trí thứ 2
Khi đó P-Q chỉ có thể ở 3-4. Vì T phải ở sau P nên P phải ở 6 hoặc 7.
=> Thỏa mãn.
Nếu tiết mục J được biểu diễn ở vị trí thứ 5 thì các tiết mục thứ 3, 4, 5, 6 lần lượt là:
Do J phải được biểu diễn ngay sau I và J được biểu diễn ở vị trí thứ 5 nên I phải được biểu diễn ở vị trí thứ 4.
Nếu H được biểu diễn ở vị trí thứ 3 và M được biểu diễn ở vị trí thứ 6 thì không thể sắp xếp được 2 tiết mục xen giữa G và K.
Do đó ta loại phương án A.
Tương tự, nếu K được biểu diễn ở vị trí thứ 3 và M được biểu diễn ở vị trí thứ 6 thì không thể sắp xếp được 2 tiết mục xen giữa G và K.
Do đó ta loại phương án B.
Tương tự, nếu G được biểu diễn ở vị trí thứ 3 và L được biểu diễn ở vị trí thứ 6 thì không thể sắp xếp được 2 tiết mục xen giữa G và K.
Do đó ta loại phương án D.
Nếu hai tiết mục N và S phải được xếp ở thứ tự xa nhau nhất thì các tiết mục thứ nhất, thứ hai và thứ ba lần lượt là
Từ các đáp án ta xét N ở vị trí 1 và S ở vị trí 7:
Vì giữa M và R có đúng 2 chỗ trống nên chỉ có thể là P-Q. Giả sử M trước R.
Mà T phải được biểu diễn sau P nên ta có: M-P-Q-R-T. Khi đó:
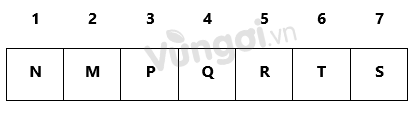
=> Đây là cách sắp xếp thứ tự thỏa mãn tất cả các dữ kiện.
=> các tiết mục thứ nhất, thứ hai và thứ ba lần lượt là N,M,P
Tiết mục K phải được biểu diễn ở vị trí thứ mấy để có thể xác định được duy nhất một vị trí biểu diễn cho tiết mục I?
Nếu tiết mục K được biểu diễn ở vị trí thứ 1 thì tiết mục I có thể được biểu diễn ở vị trí thứ 2, 5.
Do đó ta loại phương án A.
Nếu tiết mục K được biểu diễn ở vị trí thứ 3 thì tiết mục I có thể được biểu diễn ở vị trí thứ 1, 4.
Do đó ta loại phương án C.
Nếu tiết mục K được biểu diễn ở vị trí thứ 4 thì tiết mục I có thể được biểu diễn ở vị trí thứ 1, 2.
Do đó ta loại phương án D.
Tiết mục T có thể được biểu diễn ở bất kỳ vị trí nào, trừ vị trí
Vì:
- P phải được biểu diễn ngay trước Q
- T phải được biểu diễn sau P
=> T ít nhất phải biểu diễn sau P và Q.
=> T không thể biểu diễn ở vị trí thứ hai
Nếu tiết mục H và tiết mục L phải được sắp xếp biểu diễn ở thứ tự xa nhau nhất thì tiết mục K chỉ có thể biểu diễn ở vị trí nào?
Dựa vào các dữ kiện của bài toán và tiết mục H và tiết mục L phải được sắp xếp biểu diễn ở thứ tự xa nhau nhất, ta có bảng sắp xếp thứ tự biểu diễn như sau:
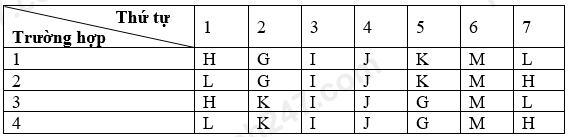
Quan sát bảng trên, ta thấy K chỉ có thể được biểu diễn ở vị trí thứ 2 hoặc thứ 5.
Nếu tiết mục M được biểu diễn ở vị trí thứ hai thì tiết mục nào được biểu diễn ở vị trí thứ ba?
Có đúng 2 tiết mục được biểu diễn xen giữa M và R. M có thể trước hoặc sau R nên ta có vị trí của M và R là:
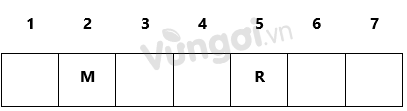
P phải được biểu diễn ngay trước Q nên P-Q chỉ có thể là 2-3 hoặc 6-7
Mà T phải được biểu diễn sau P nên P-Q chỉ có thể là 2-3 (Vì nếu là 6-7 thì không còn vị trí nào cho T)
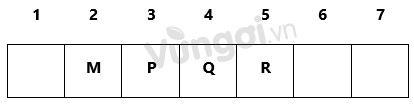
Vậy tiết mục P ở vị trí thứ ba
Nếu tiết mục G được biểu diễn ở vị trí thứ 2 và tiết mục H không được biểu diễn đầu tiên thì tiết mục nào được biểu diễn đầu tiên?
Vì giữa G và K có đúng hai tiết mục được biểu diễn xen giữa và G được biểu diễn ở vị trí thứ 2 nên K không thể được biểu diễn đầu tiên.
Do đó ta loại phương án D.
Vì J phải được biểu diễn ngay sau I, mà G được biểu diễn ở vị trí thứ 2 nên I không thể được biểu diễn đầu tiên.
Do đó ta loại phương án C.
Vì I phải biểu diễn trước M, mà I không thể được biểu diễn đầu tiên nên M cũng không thể được biểu diễn đầu tiên.
Do đó ta loại phương án B.
Nếu P đạt giải cao hơn N đúng 2 bậc thì phát biểu nào sau đây nêu đầy đủ và chính xác danh sách các học sinh có thể đạt giải nhì?
TH1: Nếu N đạt giải tư.
Vì P đạt giải cao hơn N đúng 2 bậc nên P đạt giải nhì.
TH2: Nếu Q đạt giải tư.
=> N chỉ có thể đạt giải ba hoặc năm (vì N thấp hơn P hai giải, nếu N đạt giải nhất và nhì thì không có giải cho P).
+ Nếu N đạt giải năm => P đạt giải ba.
Vì R đạt giải cao hơn M nên R đạt giải nhất và M đạt giải nhì.
+ Nếu N đạt giải ba => P đạt giải nhất.
Vì R đạt giải cao hơn M nên R đạt giải nhì và M đạt giải ba.
Vậy phát biểu nêu đầy đủ và chính xác danh sách các học sinh có thể đạt giải nhì là đáp án D: M, P, R.
Nếu M đạt giải nhì thì phát biểu nào sau đây có thể sai?
Vì M đạt giải nhì, mà R đạt giải cao hơn M => R phải đạt giải nhất.
=> Q không đạt giải nhất là phát biểu đúng => Đáp án D đúng.
Vì N hoặc Q đạt giải tư, mà P không đạt giải ba nên P phải đạt giải năm => P không đạt giải nhất và giải tư.
=> Đáp án B và C đúng.
Nếu Q đạt giải năm thì M sẽ đạt giải nào?
Vì Q đạt giải năm nên Q không đạt giải tư => N phải đạt giải tư.
Vì R đạt giải cao hơn M nên M không thể đạt giải nhất => M đạt giải nhì hoặc ba.
Nếu M đạt giải nhì => R phải đạt giải nhất => P đạt giải còn lại là giải ba (Mâu thuẫn với giả thiết P không đạt giải ba) => M phải đạt giải ba.
Danh sách nào dưới đây có thể là thứ tự các học sinh đạt giải, từ giải nhất đến giải năm?
Vì N hoặc Q đạt giải tư nên loại đáp án B.
Vì R đạt giải cao hơn M nên loại đáp án A và D.
Vậy đáp án B có thể là thứ tự các học sinh đạt giải, từ giải nhất đến giải năm.

