Giải toán tư duy bằng phương pháp loại trừ, lựa chọn và chia trường hợp
Kỳ thi ĐGNL ĐHQG Hồ Chí Minh
Nếu D đạt giải cao hơn C 3 bậc thì phát biểu nào sau đây có thể sai?
Nếu D đạt giải cao hơn C 3 bậc => có 2 trường hợp:
TH1: ? – D - ? - ? – C
Nếu A đạt giải nhất => A – D – B – E – C.
Nếu A đạt giải 3 => B – D – A – E – C.
Nếu A đạt giải 4 => B – D – E – A – C.
TH2: D - A - ? – C - ?
B đạt giải cao hơn E => D – A – B – C – E.
Đáp án A đúng: B không thể đạt giải tư.
Đáp án B đúng: Nếu D đạt giải nhất thì A đạt giải cách C 2 bậc. (TH2)
Đáp án D đúng: Nếu E đạt giải tư thì A có thể đạt giải nhất. (TH1)
=> Đáp án C.
Nếu đề xuất của mọi người đều không có mình trong đó và Duyên đưa ra ý kiến 2. Đứa đưa ra ý kiến nào?
- Duyên đưa ra ý kiến 2 nên Phương Anh chỉ có thể đưa ra đề xuất 1 hoặc 4, Vân Anh đưa ra đề xuất 1 hoặc 5, Minh Dương đưa ra đề xuất 3 hoặc 4 hoặc 5, Đức đưa ra đề xuất 1 hoặc 4 hoặc 5.
- Nếu Đức đưa ra đề xuất 1 thì Phương Anh đưa ra đề xuất 4, Vân Anh đưa ra đề xuất 5 và Minh Dương đưa ra đề xuất 3 \( \Rightarrow \) THỎA MÃN.
Nếu E đạt giải nhất, B hoặc C đạt giải nhì, C đạt giải cao hơn A. Hỏi D có thể đạt giải cao nhất là giải mấy?
E đạt giải nhất, B hoặc C đạt giải nhì => E – B/C - ? - ? - ?
=> D có thể đạt giải cao nhất là giải ba.
=> Đáp án C.
Không ai đưa ra đề nghị 3 hoặc 4 có bản thân mình trong đó. Phương Anh và Vân Anh đều không đưa ra 2 đề nghị trên. Ai đã đưa ra các đề xuất trên?
Vì không ai đưa ra đề nghị 3 hoặc 4 có bản thân mình trong đó nên Duyên sẽ là người phù hợp để đưa ra 1 trong 2 đề xuất trên.
- Phương Anh và Vân Anh đều không đưa ra 1 trong 2 đề xuất trên thì Phương Anh sẽ đưa ra đề xuất 1 và Vân Anh đưa ra đề xuất 5.
- Minh Dương có thể đưa ra 1 đề xuất trong 3 đề xuất 2, 3, 4.
- Đức không đưa ra đề xuất 3 hoặc 4 có bản thân mình trong đó. Vì vậy Đức sẽ đưa ra đề xuất số 2.
- Khi đó, Duyên chỉ đưa ra đề xuất số 3 và Minh Dương đưa ra đề xuất số 4.
Nếu A đạt giải tư thì B đạt giải nào?
A đạt giải tư => D đạt giải nhì.
=> Thứ tự nhận giải từ giải nhất đến giải năm: ? – D - ? – A - ?
Trong đó C không đạt giải nhất => có 2 trường hợp.
TH1: ? – D – C – A – ?
B đạt giải cao hơn E => B – D – C – A – E.
TH2: ? – D - ? – A – C.
B đạt giải cao hơn E => B – D – E – A – C.
Cả 2 trường hợp đều cho thấy B khi A đạt giải tư thì B đạt giải nhất.
=> Đáp án A.
Nếu đề xuất của mọi người đều không có mình trong đó và Phương Anh hoặc Vân Anh đều không đưa ra đề nghị thứ 3 thì điều nào sau đây đúng?
Vân Anh và Phương Anh không đưa ra đề nghị thứ 3 thì 3 người Đức, Vân Anh, Phương Anh đều không đưa ra đề nghị thứ 3.
- Phương Anh chỉ có thể đưa ra đề nghị 1 hoặc 4
- Vân Anh chỉ có thể đưa ra đề nghị 1 hoặc 5
- Duyên chỉ có thể là 2 hoặc 3
- Minh Dương không đưa ra đề nghị số 1
- Đức không đưa ra đề nghị số 3.
Từ đó ta có thể có cách xếp là: Vân Anh – Mình Dương – Duyên – Phương Anh – Đức thỏa mãn các điều kiện vừa liệt kê.
\( \Rightarrow \) Chọn B: Vân Anh muốn Mình Dương và Duyên đi xem xiếc.
Danh sách nào dưới đây có thể là thứ tự của các thí sinh đạt giải từ giải năm đến giải nhất:
C không đạt giải nhất => Loại A do C đạt giải nhất.
B đạt giải cao hơn E => Loại D do E đạt giải nhất, B đạt giải tư.
Loại B do đáp án bị đảo thứ tự.
=> Đáp án C.
Ai đã đi xem xiếc ngày hôm đó?
Nhận thấy rằng, Phương Anh và Duyên đi là hợp lý vì 2 người có phần đúng là Phương Anh, người còn lại có phần đúng là Duyên.
Trong trường hợp một bạn lỡ tay làm xáo trộn các tờ giấy màu khiến tờ màu vàng ở bên phải cùng, màu lục kề bên trái màu tím và màu lam ở vị trí số 3 từ trái đếm qua, tuy nhiên tờ giấy màu đỏ vẫn xếp kề trái màu lam thì khi đó?
Theo yêu cầu ta có thể sắp xếp theo 4 cách:
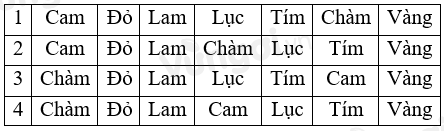
Loại A => Màu lục có thể kề phải màu chàm, cam (TH2, TH4).
Loại B => Màu vàng luôn xếp bên phải cùng nên không thể xếp bên trái màu cam.
Loại D => Màu chàm cũng có thể xếp đầu tiên (TH3, TH4).
=> Đáp án C.
Phát biểu nào sau đây là sai nếu như màu chỉ cần xếp 4 màu tím, chàm, vàng, lục?
Có 3 cách xếp:
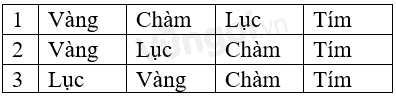
A đúng: Màu chàm luôn bên phải màu vàng (thông tin đề bài) => Loại.
C đúng: Màu lục có thể xếp tối đa 3 vị trí bảng và trừ vị trí cuối => Loại.
D đúng: (TH2 và TH3) => Loại.
Đáp án B.
Khi màu lục được xếp đầu tiên, màu cam xếp kề bên trái màu tím thì:
Có 6 cách xếp:
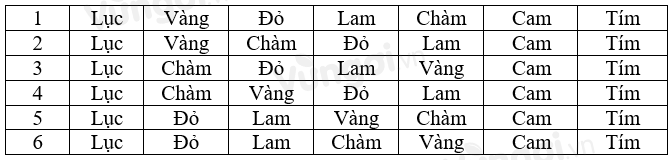
Loại A => Màu vàng và chàm xếp bên trái màu cam theo đề bài chứ không nói rằng màu vàng xếp bên trái màu chàm.
Loại B => Màu chàm kề bên phải màu lam (TH6).
Loại D => Màu lam xếp bên phải màu chàm (TH2, TH3, TH4).
Đáp án C.
Thứ tự sắp xếp nào dưới đây có thể đúng?
Màu đỏ kề bên trái màu lam => Loại A.
Màu cam bên phải màu vàng => Loại C.
Màu bên phải cùng là màu tím => Loại D
Đáp án B đúng.
Nếu có đúng 1 người về đích giữa O và F, điều nào sau đây chắc chắn sai?
Nếu O về thứ 7 thì F buộc về thứ 6 nên sẽ không có ai về trước O và sau F \( \Rightarrow \) Loại.
Chọn A.
Nếu L về đích thứ 4, những điều nào sau đây có thể đúng?
- L về thứ 4, P về sau L và trước F nên F không thể về thứ 5 \( \Rightarrow \)Loại A và B.
- P về đích thứ 3 hiển nhiên vô lý \( \Rightarrow \) Loại C.
\( \Rightarrow \)Chọn D.
Điều nào có thể đúng?
P về địch trước F
K về đích trước P
\( \Rightarrow \)K về đích trước F.
\( \Rightarrow \) Chọn D
Đâu có thể là thứ tự về đích của các bạn, theo thứ tự bên trái thì về trước?
Vì J về đích sau K nhưng trước P nên Loại C và D.
VÌ M về đích trước O nên Loại B
Chọn A
Trong cuộc thi đấu nếu D thua B thì ai có thể về cuối?
D thua B nên B đạt giải Nhì và D đạt giải ba hoặc B đạt nhất, D đạt nhì.
=> B và D không về cuối.
C thua A=> A không về cuối.
Khi đó, về cuối chỉ có thể là C.
Nếu D đạt giải Nhì thì khẳng định nào có thể sai?
Nếu B đạt giải tư, D đạt giải Nhì mà C không đạt giải Ba thì C chỉ có thể đạt giải Nhất. Do đó C đạt giải cao hơn A nên Loại \( \Rightarrow \) Chọn D.
Nếu C đạt giải tư thì A đạt giải nào?
B hoặc D đạt giải Nhì nên A không thể đạt giải Nhỉ.
Chỉ cần A đạt giải cao hơn C nên A có thể đạt giải ba hoặc giải nhất.
\( \Rightarrow \) Chọn A
Danh sách nào dưới đây có thể là thứ tự đạt giải từ cao đến thấp (từ trái qua phải)?
- C đạt giải thấp hơn A nên loại D và C.
- C không về thứ ba nên loại A.
\( \Rightarrow \) Chọn B.

