Tính đơn điệu của hàm số
Kỳ thi ĐGNL ĐHQG Hồ Chí Minh
Cho hàm số $y = f\left( x \right)$ đồng biến trên $D$ và ${x_1},{x_2} \in D$ mà ${x_1} > {x_2}$, khi đó:
Hàm số $y$ = $f\left( x \right)$ đồng biến trên $D$ nên:
Với mọi ${x_1},{x_2}$ $\in$ $D$ mà ${x_1} > {x_2}$ thì $f\left( {{x_1}} \right)$ > $f\left( {{x_2}} \right)$.
Cho hàm số $f\left( x \right)$ xác định và có đạo hàm trên $\left( {a;b} \right)$. Nếu $f'\left( x \right) < 0,\forall x \in \left( {a;b} \right)$ thì:
Sử dụng định lý về xét tính đồng biến, nghịch biến của hàm số trên một khoảng đã nêu ở phần phương pháp, ở đây khoảng $K=(a;b)$ ta được:
Hàm số $y = f\left( x \right)$ xác định và có đạo hàm $f'\left( x \right) < 0,\forall x \in \left( {a;b} \right)$ thì $f\left( x \right)$ nghịch biến trên $\left( {a;b} \right)$.
Hình dưới là đồ thị hàm số \(y = f'\left( x \right)\). Hỏi hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào dưới đây?
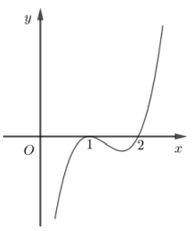
Hàm số $y = f'\left( x \right)$ dương trong khoảng $\left( {2; + \infty } \right)$
$ \Rightarrow $ Hàm số $y = f\left( x \right)$ đồng biến trên $\left( {2; + \infty } \right)$
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như hình vẽ, chọn kết luận đúng:
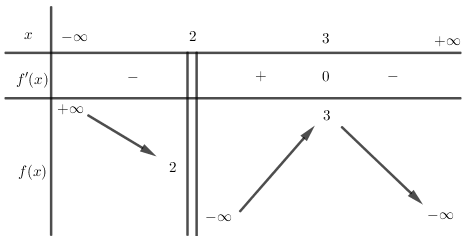
Từ bảng biến thiên ta thấy: $f'\left( x \right) > 0$ trên $\left( {2;3} \right)$ nên hàm số đồng biến trên $\left( {2;3} \right)$.
$f'\left( x \right) < 0$ trên $\left( { - \infty ;2} \right)$ và $\left( {3; + \infty } \right)$ nên hàm số nghịch biến trên các khoảng $\left( { - \infty ;2} \right)$ và $\left( {3; + \infty } \right)$.
Hàm số $y = - {x^4} - 2{x^2} + 3$ nghịch biến trên:
TXĐ: $R$.
Ta có:
\(y'=-4x^3-4x=-4x(x^2+1)\)
\(\Rightarrow y' = 0 \Leftrightarrow x = 0\)
Ta có bảng biến thiên
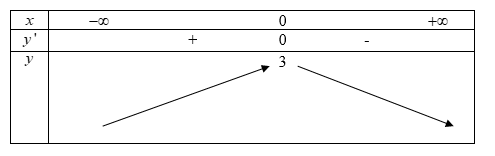
Từ bảng biến thiên ta thấy hàm nghịch biến trên khoảng $\left( {0; + \infty } \right)$.
Cho hàm số: $f(x) = - 2{x^3} + 3{x^2} + 12x - 5.$ Trong các mệnh đề sau, tìm mệnh đề sai?
$f\left( x \right) = - 2{x^3} + 3{x^2} + 12x - 5 \Rightarrow f'\left( x \right) = - 6{x^2} + 6x + 12 = 0 \Leftrightarrow x = 2;x = - 1$
Ta có: $y' < 0,\forall x \in \left( { - \infty ; - 1} \right) \cup \left( {2; + \infty } \right)$ nên hàm số nghịch biến trên các khoảng $\left( { - \infty ; - 1} \right);\left( {2; + \infty } \right)$ và $y' > 0,\forall x \in \left( { - 1 ; 2} \right)$ nên nó đồng biến trên khoảng $\left( { - 1;2} \right)$.
Đối chiếu với các đáp án đã cho ta thấy các Đáp án A, B, C đều đúng vì các khoảng đó đều là khoảng nằm trong khoảng nghịch biến hoặc đồng biến của hàm số, chỉ có đáp án D sai.
Cho hàm số $y = f\left( x \right)$ xác định và có đạo hàm $f'\left( x \right) = 2{x^2}$ trên $R$. Chọn kết luận đúng:
Ta có: $f'\left( x \right) = 2{x^2} \ge 0,\forall x \in R$ và $f'\left( x \right) = 0 \Leftrightarrow x = 0$ nên hàm số đồng biến trên $R$.
Cho hàm số $y = f\left( x \right)$ xác định và có đạo hàm trên $\left( {a;b} \right)$. Chọn kết luận đúng:
Đáp án A: Nếu $f'\left( x \right) \ge 0,\forall x\in \left( {a;b} \right)$ thì $f\left( x \right)$ chưa chắc đã đồng biến trên $\left( {a;b} \right)$, chẳng hạn hàm số $y = f\left( x \right) = 2$ có $f'\left( x \right) = 0 \ge 0,\forall x$ nhưng đây là hàm hằng nên không đồng biến, do đó A sai.
Đáp án B: Nếu $f'\left( x \right) > 0,\forall x\in \left( {a;b} \right)$ thì $f\left( x \right)$ đồng biến trên $\left( {a;b} \right)$ đúng.
Đáp án C: Nếu $f'\left( x \right) = 0,\forall x\in \left( {a;b} \right)$ thì $f\left( x \right)$ không đổi trên $\left( {a;b} \right)$, chưa chắc nó đã có giá trị bằng $0$ nên C sai.
Đáp án D: Nếu $f'\left( x \right) \le 0,\forall x\in \left( {a;b} \right)$ thì $f\left( x \right)$ không đổi trên $\left( {a;b} \right)$ sai.
Hàm số $y = {x^3} - 3{{\rm{x}}^2} + 4$ đồng biến trên:
TXĐ: $D=R$
Ta có: $y' = 3{{\rm{x}}^2} - 6{\rm{x}}$
$ \Rightarrow y' = 0 \Leftrightarrow x = 0$ hoặc $x = 2$
Ta có bảng biến thiên
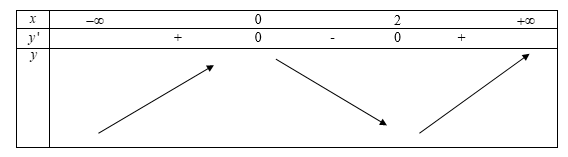
Vậy hàm số đồng biến trên các khoảng $\left( { - \infty ;0} \right)$ và $\left( {2; + \infty } \right)$.
Trong các hàm số dưới đây, hàm số nào không đồng biến trên $R?$
+) Xét đáp án A:$y = \sin x - 3x$ có: $y' = \cos x - 3.$
Với $\forall {\mkern 1mu} {\mkern 1mu} x \in R$ ta có: $ - 1 \le \cos x \le 1 \Rightarrow y' = {\rm{cosx\;}} - 3 < 0{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \forall x{\mkern 1mu} {\mkern 1mu} \in R \Rightarrow $ hàm số nghịch biến trên $R.$
Vậy hàm số ở đáp án A không đồng biến trên $R$.
+) Xét đáp án B: $y = \cos x + 2x$ có: $y' = {\rm{\;}} - \sin x + 2.$
Với $\forall {\mkern 1mu} {\mkern 1mu} x \in R$ ta có: $ - 1 \le \sin x \le 1 \Rightarrow y' = {\rm{\;}} - \sin x + 2 > 0{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \forall x{\mkern 1mu} {\mkern 1mu} \in R$
Vậy hàm số đồng biến trên $\mathbb{R}.$
+) Xét đáp án C: $y'=3x^2\ge 0, \forall x$ nên hàm số đồng biến trên $R$.
+) Xét đáp án D: $y'=5x^4\ge 0, \forall x$ nên hàm số đồng biến trên $R$.
Vậy chỉ có hàm số ở đáp án A không đồng biến trên $R$.
Cho hàm số $y = f\left( x \right)$ nghịch biến và có đạo hàm trên $\left( { - 5;5} \right)$. Khi đó:
Vì $y = f\left( x \right)$ nghịch biến trên $\left( { - 5;5} \right)$ nên $f'\left( x \right) \le 0,\forall x \in \left( { - 5;5} \right)$.
Vậy $f'\left( 0 \right) \le 0$.
Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên \(\mathbb{R}\) và có đạo hàm \(f'\left( x \right) = {x^2} - 4\). Chọn khẳng định đúng:
Ta có: \(f'\left( x \right) = {x^2} - 4 > 0 \Leftrightarrow \left[ \begin{array}{l}x > 2\\x < - 2\end{array} \right.\) và \(f'\left( x \right) = {x^2} - 4 < 0 \Leftrightarrow - 2 < x < 2\)
Do đó hàm số đồng biến trên các khoảng \(\left( { - \infty ; - 2} \right)\) và \(\left( {2; + \infty } \right)\); nghịch biến trên khoảng \(\left( { - 2;2} \right)\).
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau:
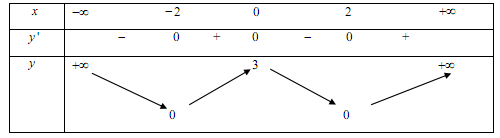
Khẳng định nào sau đây là khẳng định đúng:
A, B sai vì hàm số chỉ nghịch biến trên các khoảng $\left( { - \infty ; - 2} \right)$ và $\left( {0;2} \right)$
D sai vì hàm số chỉ đồng biến trên khoảng $\left( { - 2;0} \right)$ và $\left( {2; + \infty } \right)$
C đúng vì giá trị thấp nhất của y trên bảng biến thiên là 0.
Trong tất cả các giá trị của tham số $m$ để hàm số $y = \dfrac{1}{3}{x^3} + m{x^2} - mx - m$ đồng biến trên $R$, giá trị nhỏ nhất của $m$ là:
Ta có: $y' = {x^2} + 2m{\rm{x}} - m$
Vì $a=1>0$ nên hàm số đồng biến trên $R$
$ \Leftrightarrow {x^2} + 2m{\rm{x}} - m \ge 0$,$\forall x \in R$$ \Leftrightarrow \Delta ' = {m^2} + m \le 0 \Leftrightarrow - 1 \le m \le 0$
Tìm các giá trị của tham số $m$ sao cho hàm số $y = - {x^3} - {x^2} + mx + 1$ nghịch biến trên $R$?
Ta có : $y' = - 3{x^2} - 2x + m$
Để hàm số $y$ là hàm số nghịch biến trên $R$ thì $y' \le 0,\forall x \in R$ $ \Leftrightarrow - 3{x^2} - 2x + m \le 0,\forall x \in R$
$ \Leftrightarrow \left\{ \begin{array}{l} - 3 < 0\\\Delta ' = 1 + 3m \le 0\end{array} \right. \Leftrightarrow m \le - \dfrac{1}{3}$.
Xác định giá trị của tham số $m$ để hàm số $y = {x^3} - 3m{x^2} - m$ nghịch biến trên khoảng $\left( {0;1} \right)$.
Ta có: $y' = 3{{\rm{x}}^2} - 6m{\rm{x}}$$ \Rightarrow y' = 0 \Leftrightarrow x = 0$ hoặc $x = 2m$
Trường hợp 1: $m < 0$
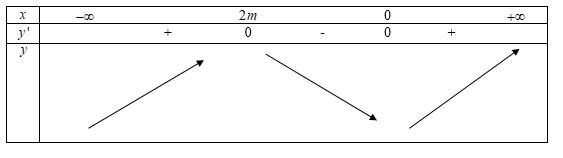
Dễ thấy hàm số trên khoảng $\left( {0;1} \right)$ đồng biến với mọi $m < 0$(loại)
Trường hợp 2: $m = 0$
Với $m=0$ thì $y'=3x^2 \ge 0$ nên hàm số đồng biến trên $R$ .
Do đó hàm số đồng biến trên $\left( {0;1} \right)$ (loại)
Trường hợp 3: $m > 0$
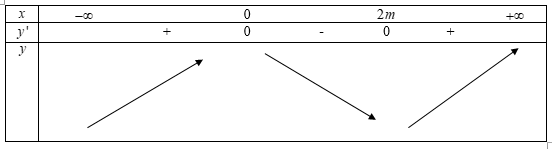
Dễ thấy hàm số trên khoảng $\left( {0;1} \right)$ nghịch biến $ \Leftrightarrow 2m \ge 1 \Leftrightarrow m \ge \dfrac{1}{2}$
Tìm $m$ để hàm số $y = \dfrac{{{x^3}}}{3} - 2m{x^2} + 4mx + 2$ nghịch biến trên khoảng $\left( { - 2;0} \right)$.
Ta có: $y' = {x^2} - 4mx + 4m$.
Hàm số nghịch biến trên $\left( { - 2;0} \right) \Rightarrow y' \leqslant 0,\forall x \in \left( { - 2;0} \right) \Leftrightarrow {x^2} - 4mx + 4m \leqslant 0,\forall x \in \left( { - 2;0} \right)$ $ \Leftrightarrow {x^2} - 4m\left( {x - 1} \right) \leqslant 0 \Leftrightarrow 4m\left( {x - 1} \right) \geqslant {x^2} \Leftrightarrow 4m \leqslant \dfrac{{{x^2}}}{{x- 1}}$ (vì $ - 2 < x < 0$)
Xét hàm $g\left( x \right) = \dfrac{{{x^2}}}{{x - 1}}$ trên $\left( { - 2;0} \right)$ ta có:
$g'\left( x \right) = \dfrac{{{x^2} - 2x}}{{{{\left( {x - 1} \right)}^2}}} = 0 \Leftrightarrow \left[ \begin{gathered}x = 0 \notin \left( { - 2;0} \right) \hfill \\x = 2 \notin \left( { - 2;0} \right) \hfill \\ \end{gathered} \right. \Rightarrow g'\left( x \right) > 0,\forall x \in \left( { - 2;0} \right)$
Do đó hàm số $y = g\left( x \right)$ đồng biến trên $\left( { - 2;0} \right)$
Suy ra \(g\left( { - 2} \right) < g\left( x \right) < g\left( 0 \right),\forall x \in \left( { - 2;0} \right)\) hay \( - \dfrac{4}{3} < g\left( x \right) < 0,\forall x \in \left( { - 2;0} \right)\)
Khi đó \(4m \le g\left( x \right),\forall x \in \left( { - 2;0} \right) \Leftrightarrow 4m \le - \dfrac{4}{3} \Leftrightarrow m \le - \dfrac{1}{3}\)
Vậy $m \leqslant - \dfrac{1}{3}$
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đạo hàm \(f'\left( x \right) = {x^2}\left( {x - 2} \right)\left( {{x^2} - 6x + m} \right)\) với mọi \(x \in \mathbb{R}\). Có bao nhiêu số nguyên \(m\) thuộc đoạn \(\left[ { - 2019;\,2019} \right]\) để hàm số \(g\left( x \right) = f\left( {1 - x} \right)\) nghịch biến trên khoảng \(\left( { - \infty ;\, - 1} \right)\)?
Ta có:
\(g'\left( x \right) = \left[ {f\left( {1 - x} \right)} \right]' = \left( {1 - x} \right)'f'\left( {1 - x} \right)= - f'\left( {1 - x} \right)\)
\(= - {\left( {1 - x} \right)^2}\left( {1 - x - 2} \right)\left[ {{{\left( {1 - x} \right)}^2} - 6\left( {1 - x} \right) + m} \right]\) \( = - {\left( {1 - x} \right)^2}\left( { - 1 - x} \right)\left( {{x^2} + 4x + m - 5} \right) = {\left( {x - 1} \right)^2}\left( {x + 1} \right)\left( {{x^2} + 4x + m - 5} \right)\)
Hàm số \(g\left( x \right)\) nghịch biến trên \(\left( { - \infty ; - 1} \right)\)
\( \Leftrightarrow g'\left( x \right) \le 0,\forall x \in \left( { - \infty ; - 1} \right) \Leftrightarrow \left( {x + 1} \right)\left( {{x^2} + 4x + m - 5} \right) \le 0,\forall x \in \left( { - \infty ; - 1} \right)\)
\( \Leftrightarrow {x^2} + 4x + m - 5 \ge 0,\forall x \in \left( { - \infty ; - 1} \right)\) (do \(x + 1 < 0,\forall x \in \left( { - \infty ; - 1} \right)\))
\( \Leftrightarrow h\left( x \right) = {x^2} + 4x - 5 \ge - m\,\,\forall x \in \left( { - \infty ; - 1} \right)\)
\(\Leftrightarrow - m \le \mathop {\min }\limits_{\left( { - \infty ; - 1} \right]} h\left( x \right)\).
Ta có \(h'\left( x \right) = 2x + 4 = 0 \Leftrightarrow x = - 2\).
BBT:
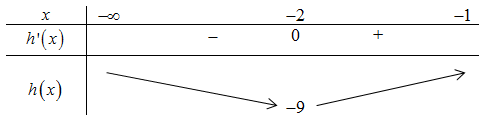
Dựa vào BBT ta có \( - m \le - 9 \Leftrightarrow m \ge 9\).
Mà \(m \in \left[ { - 2019;2019} \right]\) và \(m\) nguyên nên \(m \in \left[ {9;10;11;...;2019} \right]\) hay có \(2019 - 9 + 1 = 2011\) giá trị của \(m\) thỏa mãn.
Cho \(f\left( x \right)\) mà đồ thị hàm số \(y = f'\left( x \right)\) như hình bên. Hàm số \(y = f\left( {x - 1} \right) + {x^2} - 2x\) đồng biến trên khoảng?
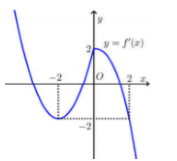
Ta có: \(y' = f'\left( {x - 1} \right) + 2x - 2 = 0\) \( \Leftrightarrow f'\left( {x - 1} \right) + 2\left( {x - 1} \right) = 0\).
Đặt \(t = x - 1\) ta có \(f'\left( t \right) + 2t = 0\) \( \Leftrightarrow f'\left( t \right) - \left( { - 2t} \right) = 0\).
Vẽ đồ thị hàm số \(y = f'\left( t \right)\) và \(y = - 2t\) trên cùng mặt phẳng tọa độ ta có:
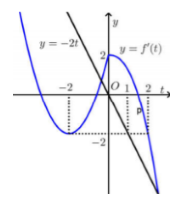
Xét \(y' \ge 0 \Leftrightarrow f'\left( t \right) \ge - 2t \Rightarrow \) Đồ thị hàm số \(y = f'\left( t \right)\) nằm trên đường thẳng \(y = - 2t\).
Xét \(x \in \left( {1;2} \right) \Rightarrow t \in \left( {0;1} \right) \Rightarrow \) thỏa mãn.
Xét \(x \in \left( { - 1;0} \right) \Rightarrow t \in \left( { - 2; - 1} \right) \Rightarrow \) Không thỏa mãn.
Xét \(x \in \left( {0;1} \right) \Rightarrow t \in \left( { - 1;0} \right) \Rightarrow \) Không thỏa mãn.
Xét \(x \in \left( { - 2; - 1} \right) \Rightarrow t \in \left( { - 3; - 2} \right) \Rightarrow \) Không thỏa mãn.
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình bên:

Hàm số \(y = - 2f\left( x \right)\) đồng biến trên khoảng:
Dựa vào đồ thị hàm số ta có hàm số \(y = f\left( x \right)\) đồng biến trên các khoảng \(\left( { - \infty ;\,0} \right)\) và \(\left( {2;\, + \infty } \right).\)
Hàm số \(y = f\left( x \right)\) nghịch biến trên \(\left( {0;\,\,2} \right).\)
Xét hàm số: \(y = - 2f\left( x \right)\) ta có: \(y' = - 2f'\left( x \right).\)
Hàm số đồng biến \( \Leftrightarrow - 2f'\left( x \right) \ge 0 \Leftrightarrow f'\left( x \right) \le 0 \Leftrightarrow 0 \le x \le 2.\)
Vậy hàm số \(y = - 2f\left( x \right)\) đồng biến \( \Leftrightarrow x \in \left[ {0;\,2} \right].\)

