Các bài toán về đường thẳng và mặt cầu
Kỳ thi ĐGNL ĐHQG Hồ Chí Minh
Trong không gian với hệ tọa độ $Oxyz$, cho mặt cầu \((S):{x^2} + {\left( {y + 1} \right)^2} + z{}^2 = {R^2}\). Điều kiện của bán kính $R$ để trục $Ox$ tiếp xúc với $(S)$ là:
Tọa độ giao điểm của $(S)$ và $Ox$ là nghiệm của hệ $\left\{ \begin{array}{l}{x^2} + {\left( {y + 1} \right)^2} + z{}^2 = {R^2}\\x = t\\y = 0\\z = 0\end{array} \right.$(*)
$(S)$ tiếp xúc với $Ox$ khi và chỉ khi (*) có nghiệm kép \( \Leftrightarrow {t^2} + 1 = {R^2}\) có nghiệm kép \( \Leftrightarrow {R^2} - 1 = 0 \Leftrightarrow R = 1\)
Trong không gian với hệ tọa độ $Oxyz$, cho điểm \(A(1; - 2;3)\) và đường thẳng $d$ có phương trình \(\dfrac{{x + 1}}{2} = \dfrac{{y - 2}}{1} = \dfrac{{z + 3}}{{ - 1}}\). Tính đường kính của mặt cầu $(S)$ có tâm $A$ và tiếp xúc với đường thẳng $d$.
Phương trình mặt cầu $(S) $ có dạng ${(x - 1)^2} + {(y + 2)^2} + (z - 3){}^2 = {R^2}$
Phương trình tham số của $d$ là: \(d:\left\{ \begin{array}{l}x = - 1 + 2t\\y = 2 + t\\z = - 3 - t\end{array} \right.\)
Tọa độ giao điểm của $(S)$ và $d$ là nghiệm của hệ \(\left\{ \begin{array}{l}{(x - 1)^2} + {(y + 2)^2} + {(z - 3)^2} = {R^2}\\x = - 1 + 2t\\y = 2 + t\\z = - 3 - t\end{array} \right.\) (*)
$(S)$ tiếp xúc với $d$ khi và chỉ khi $(*)$ có nghiệm kép
\( \Leftrightarrow {( - 2 + 2t)^2} + {(4 + t)^2} + {( - 6 - t)^2} = {R^2}\) có nghiệm kép
\( \Leftrightarrow 6{t^2} + 12t + 56 - R{}^2 = 0\) có nghiệm kép
\( \Leftrightarrow \Delta ' = {\left( { - 6} \right)^2} - 6.(56 - R{}^2) = 0 \Leftrightarrow 6{R^2} - 300 = 0 \Leftrightarrow {R^2} = 50 \Leftrightarrow R = 5\sqrt 2 \)
Suy ra đường kính của mặt cầu $(S)$ là \(10\sqrt 2 \).
Trong không gian với hệ tọa độ $Oxyz$, phương trình mặt cầu $(S)$ có tâm \(I(2;0;1)\) và tiếp xúc với đường thẳng \(d:\dfrac{{x - 1}}{1} = \dfrac{y}{2} = \dfrac{{z - 2}}{1}\) là:
Phương trình mặt cầu $(S)$ có dạng ${(x - 2)^2} + {y^2} + (z - 1){}^2 = {R^2}$
Phương trình tham số của $d$ là: \(d:\left\{ \begin{array}{l}x = 1 + t\\y = 2t\\z = 2 + t\end{array} \right.\)
Tọa độ giao điểm của $(S)$ và $d$ là nghiệm của hệ $\left\{ \begin{array}{l}{(x - 2)^2} + {y^2} + (z - 1){}^2 = {R^2}\\x = 1 + t\\y = 2t\\z = 2 + t\end{array} \right.(*)$
$(S)$ tiếp xúc với $d$ khi và chỉ khi $(*)$ có nghiệm kép
\( \Leftrightarrow {(t - 1)^2} + {(2t)^2} + (1 + t){}^2 = {R^2}\) có nghiệm kép
\( \Leftrightarrow 6{t^2} + 2 = {R^2}\) có nghiệm kép \( \Leftrightarrow {R^2} = 2\)
Trong không gian với hệ tọa độ $Oxyz$, cho đường thẳng \(\Delta \) có phương trình \(x = y = z\). Trong bốn phương trình mặt cầu dưới đây, phương trình mặt cầu không có hai điểm chung phân biệt với \(\Delta \) là:
\(A \in \Delta \Rightarrow A\left( {t;t;t} \right)\).
- Thay\(A\left( {t;t;t} \right)\) vào \({x^2} + {y^2} + {z^2} + x + y + z - 6 = 0\) ta có \(3{t^2} + 3t - 6 = 0\). Phương trình có 2 nghiệm phân biệt. Loại
- Thay\(A\left( {t;t;t} \right)\) vào \({x^2} + {y^2} + {z^2} + 2x - 4y + 2z - 3 = 0\) ta có \(3{t^2} - 3 = 0\) . Phương trình có 2 nghiệm phân biệt. Loại
- Thay\(A\left( {t;t;t} \right)\) vào \({x^2} + {y^2} + {z^2} - 2x + 3y + 5z + 3 = 0\) ta có \(3{t^2} + 6t + 3 = 0\) . Phương trình có nghiệm kép. Thỏa mãn
- Thay\(A\left( {t;t;t} \right)\) vào \({x^2} + {y^2} + {z^2} - 7x - 2z + 6 = 0\) ta có \(3{t^2} - 9t + 6 = 0\) . Phương trình có 2 nghiệm phân biệt. Loại
Trong bốn phương trình mặt cầu dưới đây, phương trình mặt cầu có điểm chung với trục $Oz$ là:
\(A \in Oz \Rightarrow A\left( {0;0;t} \right)\).
- Thay\(A\left( {0;0;t} \right)\) vào \({x^2} + {y^2} + {z^2} + 4x - 8y + 2z + 2 = 0\) ta có \({t^2} + 2t + 2 = 0\). Phương trình vô nghiệm. Loại
- Thay\(A\left( {0;0;t} \right)\) vào \({x^2} + {y^2} + {z^2} + 2x - 4y - 2z + 2 = 0\) ta có \({t^2} - 2t + 2 = 0\) . Phương trình vô nghiệm. Loại
- Thay\(A\left( {0;0;t} \right)\) vào \({x^2} + {y^2} + {z^2} + x - 2y + z + 1 = 0\) ta có \({t^2} + t + 1 = 0\) . Phương trình vô nghiệm. Loại
- Thay\(A\left( {0;0;t} \right)\) vào \({x^2} + {y^2} + {z^2} - 2x + 4y + 4z + 4 = 0\) ta có \({t^2} + 4t + 4 = 0\). Phương trình có nghiệm kép. Thỏa mãn
Trong không gian với hệ tọa độ $Oxyz$, cho mặt cầu $(S)$ có phương trình
\({(x - 1)^2} + {(y + 2)^2} + {(z - 3)^2} = 50\). Trong số các đường thẳng sau, mặt cầu $(S)$ tiếp xúc với đường thẳng nào.
$(S)$ có tâm \(I(1; - 2;3)\) và \(R = \sqrt {50} \)
Gọi $M$ là hình chiếu của $I$ lên trục $Ox$.
Suy ra \(M(1;0;0) \Rightarrow d(I,{\rm{Ox) = MI = }}\sqrt {{2^2} + {3^2}} = \sqrt {13} \ne R \Rightarrow \), loại B.
Gọi $N$ là hình chiếu của $I$ lên trục $Oy$.
Suy ra $N(0; - 2;0) \Rightarrow d(I,{\text{Oy) = NI = }}\sqrt {{1^2} + {3^2}} = \sqrt {10} \ne R \Rightarrow $ loại C
Gọi $P$ là hình chiếu của $I$ lên trục $Oz$.
Suy ra \(P(0;0;3) \Rightarrow d(I,{\rm{Oz) = PI = }}\sqrt {{1^2} + {2^2}} = \sqrt 5 \ne R \Rightarrow \), loại D
Xét đường thẳng $d$ có phương trình \(\left\{ \begin{array}{l}x = 1 + t\\y = 2\\z = 3 + 2t\end{array} \right.\) và mặt cầu $(S)$ có phương trình \({(x - 1)^2} + {(y - 2)^2} + {(z - 3)^2} = 4\). Nhận xét nào sau đây đúng.
Giải hệ:
\(\left\{ \begin{array}{l}x = 1 + t\\y = 2\\z = 3 + 2t\\{(x - 1)^2} + {(y - 2)^2} + {(z - 3)^2} = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1 + t\\y = 2\\z = 3 + 2t\\{t^2} + {(2t)^2} = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1 + t\\y = 2\\z = 3 + 2t\\5{t^2} = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t = \pm \sqrt {\dfrac{4}{5}} \\x = 1 + t\\y = 2\\z = 3 + 2t\end{array} \right.\)
Suy ra $d $ cắt $(S)$ tại hai điểm phân biệt.
Mặt khác $(S)$ có tâm \(I(1;2;3) \in d\) nên $d$ qua tâm của mặt cầu.
Do đó $AB$ đạt GTLN.
Trong không gian với hệ tọa độ $Oxyz$, cho mặt cầu \((S):{\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} + \left( {z - 3} \right){}^2 = 9\) và đường thẳng \(d:x - 1 = \dfrac{{y - 2}}{2} = \dfrac{{z - 4}}{3}\). $(d)$ cắt $(S)$ tại hai điểm phân biệt $A$ và $B$. Khi đó $AB$ bằng:
Tham số hóa phương trình đường thẳng $d$ ta được: $d:\left\{ \begin{array}{l}x = t + 1\\y = 2 + 2t\\z = 4 + 3t\end{array} \right.$
Giả sử $A$ là giao điểm của $(d)$ và $(P)$.
Vì $A \in d:\left\{ \begin{array}{l}x = t + 1\\y = 2 + 2t\\z = 4 + 3t\end{array} \right.$ nên ta có:$A\left( {t + 1;2 + 2t;4 + 3t} \right)$
Mặt khác \(A \in (S)\) nên ta có
\(\begin{array}{l}{\left( {t + 1 - 1} \right)^2} + {\left( {2 + 2t + 2} \right)^2} + {\left( {4 + 3t - 3} \right)^2} = 9\\ \Leftrightarrow {t^2} + {\left( {4 + 2t} \right)^2} + {\left( {1 + 3t} \right)^2} = 9\\ \Leftrightarrow 14{t^2} + 22t + 8 = 0\\ \Leftrightarrow \left[ \begin{array}{l}t = - 1\\t = - \dfrac{4}{7}\end{array} \right. \Rightarrow \left[ \begin{array}{l}A\left( {0;0;1} \right)\\B\left( {\dfrac{3}{7};\dfrac{6}{7};\dfrac{{16}}{7}} \right)\end{array} \right. \Rightarrow AB = \sqrt {{{\left( {\dfrac{3}{7}} \right)}^2} + {{\left( {\dfrac{6}{7}} \right)}^2} + {{\left( {\dfrac{{16}}{7} - 1} \right)}^2}} = \dfrac{{\sqrt {126} }}{7}\end{array}\)
Trong không gian với hệ tọa độ $Oxyz$, phương trình mặt cầu $(S)$ có tâm \(I(3; - 2;0)\) và cắt trục $Oy $ tại hai điểm $A, B$ mà \(AB = 8\) là
Gọi $H$ là hình chiếu vuông góc của $I$ lên \( Oy \Rightarrow H(0; - 2;0)\)
$ \Rightarrow \overrightarrow {IH} = \left( { - 3;0;0} \right) \Rightarrow IH = 3$
Mặt khác ta có: \(AH = \dfrac{{AB}}{2} = 4\)
Suy ra \({R^2} = A{H^2} + H{I^2} = {4^2} + {3^2} = 25\)
$(S)$ có tâm \(I(3; - 2;0)\) và bán kính $R$ với \({R^2} = 25\). Suy ra:
\((S):{(x - 3)^2} + {(y + 2)^2} + {z^2} = 25\)
Trong không gian với hệ tọa độ $Oxyz$, cho hai đường thẳng \(d:\left\{ \begin{array}{l}x = 2t\\y = t\\z = 4\end{array} \right.\) và \(d':\left\{ \begin{array}{l}x = t'\\y = 3 - t'\\z = 0\end{array} \right.\) . Phương trình mặt cầu có đường kính là đoạn thẳng vuông góc chung của hai đường thẳng $d$ và $d'$ là:
Lấy ${\rm{A}} \in {\rm{d}} \Rightarrow {\rm{A}}\left( {2a;a;4} \right)$ và \(B \in d' \Rightarrow B\left( {b;3 - b;0} \right)\). Ta có: \(\overrightarrow {AB} = \left( {b - 2a;3 - a - b; - 4} \right)\)
$AB$ là đoạn vuông góc chung của hai đường thẳng $d$ và $d’$ khi và chỉ khi
\(\left\{ \begin{array}{l}\overrightarrow {AB} .\overrightarrow {{u_d}} = 0\\\overrightarrow {AB} .\overrightarrow {{u_{d'}}} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2.\left( {b - 2a} \right) + 1.\left( {3 - a - b} \right) + 0.\left( { - 4} \right) = 0\\1.\left( {b - 2a} \right) - 1.\left( {3 - a - b} \right) + 0.\left( { - 4} \right) = 0\end{array} \right. \\ \Leftrightarrow \left\{ \begin{array}{l} - 5a + b + 3 = 0\\ - a + 2b - 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 2\end{array} \right.\)
Suy ra ${\rm{A}}\left( {2;1;4} \right)$, \(B\left( {2;1;0} \right)\) và \(\overrightarrow {AB} = \left( {0;0; - 4} \right)\)
Phương trình mặt cầu có đường kính là đoạn thẳng vuông góc chung của hai đường thẳng $d$ và $d'$
Có tâm $I$ là trung điểm của $AB$ và bán kính \(R = \dfrac{{AB}}{2}\).
Ta có \(I\left( {2;1;2} \right)\) và \(R = \dfrac{{AB}}{2} = \dfrac{4}{2} = 2\)
Vậy ta có \({(x - 2)^2} + {(y - 1)^2} + {(z - 2)^2} = 4\)
Trong không gian với hệ tọa độ $Oxyz$, cho mặt cầu $(S)$ có phương trình \({(x + 1)^2} + {(y - 1)^2} + {(z - 2)^2} = 4\). Phương trình nào sau đây là phương trình của mặt cầu đối xứng với mặt cầu $(S)$ qua trục $Oz$.
Bước 1: Gọi $(S’)$ là mặt cầu đối xứng với mặt cầu $(S)$ qua trục $Oz$.
$(S)$ có tâm \(I( - 1;1;2)\) và \(R = 2\)
Bước 2: Tìm $J$ là điểm đối xứng của tâm mặt cầu $(S)$ qua $Oz$.
Lấy đối xứng điểm $I$ qua trục $Oz$ ta được \(J(1; - 1;2)\).
Bước 3: Tìm mặt cầu $(S’)$
$(S’)$ có tâm $J$ và bán kính $R$ có phương trình là: \({(x - 1)^2} + {(y + 1)^2} + {(z - 2)^2} = 4\)
Trong không gian với hệ tọa độ ${\rm{Ox}}yz$. Hãy viết phương trình mặt cầu $(S)$ có tâm \(I(2\,;\,0;1)\) và tiếp xúc với đường thẳng \(d: \dfrac{{x - 1}}{1} = \dfrac{y}{2} = \dfrac{{z - 2}}{1}\).
\(\overrightarrow {{u_d}} = (1;2;1)\) . Lấy điểm \( M( 1;0;2) \in d\) ;
\(\begin{array}{l}\overrightarrow {MI} = ( - 1;0;1) \Rightarrow \left[ {\overrightarrow {MI} ,\overrightarrow u } \right] = ( - 2;2; - 2)\\R = d(I,d) = \dfrac{{\left| {\left[ {\overrightarrow {MI} ,\overrightarrow u } \right]} \right|}}{{\left| {\overrightarrow u } \right|}} = \dfrac{{\sqrt {{{(2)}^2} + {2^2} + {{( - 2)}^2}} }}{{\sqrt {{1^2} + {2^2} + {1^2}} }} = \sqrt 2 \end{array}\)
Vậy phương trình mặt cầu tâm $I ( 2; 0; 1)$ bán kính \(\sqrt 2 \) là:
\({\left( {x - 2} \right)^2} + {y^2} + {\left( {z - 1} \right)^2} = 2\) .
Trong không gian với hệ tọa độ $Oxyz$, cho đường thẳng $d:\dfrac{{x - 1}}{{ - 1}} = \dfrac{{y - 2}}{1} = \dfrac{{z + 1}}{2}$, điểm $A (2; -1; 1)$. Gọi $I$ là hình chiếu vuông góc của $A$ lên $d$. Viết phương trình mặt cầu $(C)$ có tâm $I$ và đi qua $A$.
Phương trình mặt phẳng $\left( P \right)$ qua $A$ , vuông góc $\left( d \right)$ là:
$ - 1.\left( {x - 2} \right) + 1.\left( {y + 1} \right) + 2.\left( {z - 1} \right) = 0 \Leftrightarrow -x + y + 2z + 1 = 0$
Gọi \(I\left( {1 - t;2 + t; - 1 + 2t} \right) = d \cap \left( P \right)\), khi đó:
\( - \left( {1 - t} \right) + \left( {2 + t} \right) + 2\left( { - 1 + 2t} \right) + 1 = 0 \Leftrightarrow t = 0 \Rightarrow I\left( {1;2; - 1} \right)\)
Có $I{A^2} = 14$. Phương trình mặt cầu là:
${\left( {x-1} \right)^2} + {\left( {y-2} \right)^2} + {\left( {z + 1} \right)^2} = 14$
Trong không gian với hệ tọa độ $Oxyz$, cho mặt cầu $\left( S \right):{x^2} + {y^2} + {z^2} - 2{\rm{x}} - 4y + 4{\rm{z}} - 16 = 0$ và đường thẳng $d:\dfrac{{x - 1}}{1} = \dfrac{{y + 3}}{2} = \dfrac{z}{2}$. Mặt phẳng nào trong các mặt phẳng sau chứa $d$ và tiếp xúc với mặt cầu $(S)$.
Ta xét mặt cầu $(S):{(x - 1)^2} + {(y - 2)^2} + {(z + 2)^2} = 25$
$\Rightarrow I(1;2; - 2);R = 5$
Điểm $A(1;-3;0)$ thuộc $d$ nên $A \in (P)$ và $d(I;(P)) = 5$ nên thử các đáp án ta thấy C đúng.
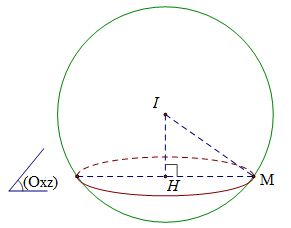
Trong không gian với hệ tọa độ $Oxyz$, cho mặt cầu $(S)$ có tâm $I$ thuộc đường thẳng \(\Delta :\dfrac{x}{1} = \dfrac{{y + 3}}{1} = \dfrac{z}{2}\) . Biết rằng mặt cầu $(S)$ có bán kính bằng \(2\sqrt 2 \) và cắt mặt phẳng $(Oxz)$ theo một đường tròn có bán kính $2$. Tìm tọa độ tâm $I$.
Tâm $I$ thuộc đường thẳng $d$ nên $I\left( {t; - 3 + t;2t} \right)$
Phương trình mặt phẳng $\left( {{\rm{Oxz}}} \right):y = 0$
Ta có bán kính mặt cầu $IM = 2\sqrt 2 $, mặt cầu cắt mặt phẳng $(Oxz)$ theo đường tròn có bán kính $HM=2$ suy ra $d\left( {I,\left( {Oxz} \right)} \right) = IH = \sqrt {I{M^2} - H{M^2}} = \sqrt {8 - 4} = 2$
Ta có $\left| { - 3 + t} \right| = 2 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{ - 3 + t = 2}\\{ - 3 + t = - 2}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{t = 5 \Rightarrow I\left( {5;2;10} \right)}\\{t = 1 \Rightarrow I\left( {1; - 2;2} \right)}\end{array}} \right.$
Trong không gian với hệ tọa độ $Oxyz$, cho mặt cầu $(S)$ có phương trình: \({x^2} + {y^2} + {z^2} - 2x + 4y - 2z - 3 = 0\) và đường thẳng \(\Delta :\,\,\dfrac{x}{2} = \dfrac{{y + 1}}{{ - 2}} = z\) . Mặt phẳng $(P)$ vuông góc với \(\Delta \) và tiếp xúc với $(S)$ có phương trình là
Tâm mặt cầu $I(1;-2;1)$, bán kính $R=3$.
Mặt phẳng $(P)$ vuông góc với $\Delta $ có phương trình dạng $2{\rm{x - }}2y + z + D = 0$
Vì $(P)$ tiếp xúc với mặt cầu nên ${\rm{d}}\left( {I,\left( P \right)} \right) = R \Rightarrow \left| {D - 7} \right| = 9 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{D = -2}\\{D = 16}\end{array}} \right.$
Phương trình $(P)$ là $2x-2y+z-2=0; 2x-2y+z+16=0$.
Trong không gian với hệ tọa độ $Oxyz$ , cho đường thẳng \(d:\left\{ \begin{array}{l}x = t\\y = - 1\\z = - t\end{array} \right.\) và 2 mặt phẳng $(P)$ và $(Q)$ lần lượt có phương trình $x + 2y + 2z + 3 = 0;x + 2y + 2z + 7 = 0$. Viết phương trình mặt cầu $(S)$ có tâm$I$ thuộc đường thẳng $d$, tiếp xúc với hai mặt phẳng $(P)$ và $(Q)$.
Ta có
$\begin{array}{l}I \in d \Rightarrow I\left( {t; - 1; - t} \right)\\ \Rightarrow d\left( {I,\left( P \right)} \right) = d\left( {I,\left( Q \right)} \right) \Leftrightarrow \dfrac{{\left| {t - 2 - 2t + 3} \right|}}{{\sqrt {{1^2} + {2^2} + {2^2}} }} = \dfrac{{\left| {t - 2 - 2t + 7} \right|}}{{\sqrt {{1^2} + {2^2} + {2^2}} }} \\ \Leftrightarrow \left| { - t + 1} \right| = \left| { - t + 5} \right| \Leftrightarrow t = 3\\ \Rightarrow I\left( {3; - 1; - 3} \right)\\ \Rightarrow R = \dfrac{{\left| { - 3 + 1} \right|}}{{\sqrt 9 }} = \dfrac{2}{3}\\ \Rightarrow (S):{\left( {x - 3} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z + 3} \right)^2} = \dfrac{4}{9}\end{array}$
Trong không gian với hệ tọa độ $Oxyz$, cho đường thẳng \(d:\dfrac{x}{2} = \dfrac{{z - 3}}{1} = \dfrac{{y - 2}}{1}\) và hai mặt phẳng $(P): x – 2y + 2z = 0. (Q): x – 2y + 3z -5 =0$. Mặt cầu $(S)$ có tâm $I $ là giao điểm của đường thẳng $d$ và mặt phẳng $(P)$. Mặt phẳng $(Q)$ tiếp xúc với mặt cầu $(S)$. Viết phương trình của mặt cầu $(S)$.
\(I \in d \Rightarrow I\left( {2t;3 + t;2 + t} \right)\)
\(I \in \left( P \right) \Rightarrow 2t - 2(3 + t) + 2(2 + t) = 0 \Leftrightarrow t = 1 \Rightarrow I\left( {2;4;3} \right)\)
Do $(Q)$ tiếp xúc với mặt cầu $(S)$ nên \(R = d\left( {I;\left( Q \right)} \right) = \dfrac{{|2 - 2.4 + 3.3 - 5|}}{{\sqrt {1 + {2^2} + {3^2}} }} = \sqrt {\dfrac{2}{7}} \)
\( \Rightarrow \left( S \right):{\left( {x - 2} \right)^2} + {\left( {y - 4} \right)^2} + {\left( {z - 3} \right)^2} = \dfrac{2}{7}\)
Trong không gian Oxyz, cho 3 điểm \(A\left( {0;1;1} \right),{\mkern 1mu} B\left( {3;0; - 1} \right),{\mkern 1mu} C\left( {0;21; - 19} \right)\) và mặt cầu \(\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 1} \right)^2} = 1\). Điểm M thuộc mặt cầu (S) sao cho tổng \(3M{A^2} + 2M{B^2} + M{C^2}\) đạt giá trị nhỏ nhất, khi đó, độ dài vectơ \(\overrightarrow {OM} \) là
+) Mặt cầu \(\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 1} \right)^2} = 1\) có tâm \(J\left( {1;1;1} \right)\), bán kính \(R = 1\).
+) Tìm \(I\):
\(3\overrightarrow {IA} + 2\overrightarrow {IB} + \overrightarrow {IC} = \vec 0 \) \(\Leftrightarrow 6\overrightarrow {IA} + 2\overrightarrow {AB} + \overrightarrow {AC} = \vec 0 \) \(\Leftrightarrow \overrightarrow {IA} = - \dfrac{{2\overrightarrow {AB} + \overrightarrow {AC} }}{6}\)
\(A\left( {0;1;1} \right),{\mkern 1mu} B\left( {3;0; - 1} \right),{\mkern 1mu} C\left( {0;21; - 19} \right) \) \(\Rightarrow \overrightarrow {IA} \left( { - {x_I};1 - {y_I};1 - {z_I}} \right),{\mkern 1mu} {\mkern 1mu} \overrightarrow {AB} \left( {3; - 1; - 2} \right),\) \({\mkern 1mu} {\mkern 1mu} \overrightarrow {AC} \left( {0;20; - 20} \right)\)
\( \Rightarrow \left\{ \begin{array}{l} - {x_I} = - \dfrac{{2.3 + 0}}{6}\\1 - {y_I} = - \dfrac{{2.\left( { - 1} \right) + 20}}{6}\\1 - {z_I} = - \dfrac{{2.\left( { - 2} \right) + \left( { - 20} \right)}}{6}\end{array} \right.\) \( \Rightarrow I\left( {1;4; - 3} \right)\)
+) Ta có:
\(\begin{array}{l}3M{A^2} + 2M{B^2} + M{C^2} \\= 3{\left( {\overrightarrow {MI} + \overrightarrow {IA} } \right)^2} + 2{\left( {\overrightarrow {MI} + \overrightarrow {IB} } \right)^2} + {\left( {\overrightarrow {MI} + \overrightarrow {IC} } \right)^2}\\ = 6M{I^2} + 3I{A^2} + 2I{B^2} + I{C^2} \\+ 2.\overrightarrow {MI} .\left( {3\overrightarrow {IA} + 2\overrightarrow {IB} + \overrightarrow {IC} } \right) \\= 6M{I^2} + 3I{A^2} + 2I{B^2} + I{C^2} + 2.\overrightarrow {MI} .\vec 0\\ = 6M{I^2} + 3I{A^2} + 2I{B^2} + I{C^2}\end{array}\)
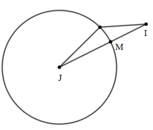
Để tổng trên là nhỏ nhất thì MI nhỏ nhất \( \Rightarrow M\) là giao điểm của đoạn thẳng IJ và mặt cầu \(\left( S \right)\).
\(\overrightarrow {JI} = \left( {0;3; - 4} \right)\)\( \Rightarrow \) Tọa độ điểm \(M\) thuộc đoạn IJ có dạng \(\left( {1;1 + 3t;1 - 4t} \right),{\mkern 1mu} {\mkern 1mu} t \in \left[ {0;1} \right]\)
Mặt khác \(M \in \left( S \right) \) \(\Rightarrow {\left( {1 - 1} \right)^2} + {\left( {1 - \left( {1 + 3t} \right)} \right)^2} + {\left( {1 - \left( {1 - 4t} \right)} \right)^2} = 1\)
\( \Leftrightarrow {t^2} = \dfrac{1}{{25}} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\rm{\;}}&{t = \dfrac{1}{5}}\\{}&{t = - \dfrac{1}{5}{\mkern 1mu} (L)}\end{array}} \right. \Leftrightarrow t = \dfrac{1}{5}\)\( \Rightarrow M\left( {1;\dfrac{8}{5};\dfrac{1}{5}} \right) \Rightarrow OM = \dfrac{{3\sqrt {10} }}{5}\).
Trong không gian với hệ tọa độ $Oxyz$, cho mặt phẳng \((P):2x - y - 2z + 1 = 0\) và ba điểm\(A(1; - 2;0)\), \(B(1;0; - 1)\) và \(C(0;0; - 2)\). Hỏi có tất cả bao nhiêu mặt cầu có tâm thuộc mặt phẳng $(P)$ và tiếp xúc với ba đường thẳng $AB, AC, BC$?
Ta có:
\(\begin{array}{l}\overrightarrow {AB} = \left( {0;2; - 1} \right)\\\overrightarrow {AC} = \left( { - 1;2; - 2} \right)\\\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( { - 2;1;2} \right)\end{array}\)
Mặt phẳng $(ABC)$ có vecto pháp tuyến là \(\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( { - 2;1;2} \right)\). Suy ra $(P) // (ABC)$
Trên mặt phẳng $(ABC) $ có $4$ điểm $M, N, P, Q$ cách đều $AB, BC, AC $ là tâm đường tròn nội tiếp, $3$ tâm đường tròn bàng tiếp các góc $A, B, C$ do đó có $4$ điểm \(M',N',P',Q'\) trên mặt phẳng $(P)$ là hình chiếu vuông góc của $M, N, P, Q$ trên $(P)$ thỏa mãn tính chất cách đều $AB, BC, AC$.
Tương ứng có $4 $ mặt cầu tâm \(M',N',P',Q'\) thỏa mãn yêu cầu bài toán.

