Trong không gian Oxyz, cho 3 điểm A(0;1;1),B(3;0;−1),C(0;21;−19) và mặt cầu (S):(x−1)2+(y−1)2+(z−1)2=1. Điểm M thuộc mặt cầu (S) sao cho tổng 3MA2+2MB2+MC2 đạt giá trị nhỏ nhất, khi đó, độ dài vectơ →OM là
Trả lời bởi giáo viên
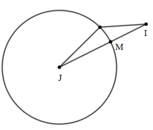
+) Mặt cầu (S):(x−1)2+(y−1)2+(z−1)2=1 có tâm J(1;1;1), bán kính R=1.
+) Tìm I:
3→IA+2→IB+→IC=→0 ⇔6→IA+2→AB+→AC=→0 ⇔→IA=−2→AB+→AC6
A(0;1;1),B(3;0;−1),C(0;21;−19) ⇒→IA(−xI;1−yI;1−zI),→AB(3;−1;−2), →AC(0;20;−20)
⇒{−xI=−2.3+061−yI=−2.(−1)+2061−zI=−2.(−2)+(−20)6 ⇒I(1;4;−3)
+) Ta có:
3MA2+2MB2+MC2=3(→MI+→IA)2+2(→MI+→IB)2+(→MI+→IC)2=6MI2+3IA2+2IB2+IC2+2.→MI.(3→IA+2→IB+→IC)=6MI2+3IA2+2IB2+IC2+2.→MI.→0=6MI2+3IA2+2IB2+IC2
Để tổng trên là nhỏ nhất thì MI nhỏ nhất ⇒M là giao điểm của đoạn thẳng IJ và mặt cầu (S).
→JI=(0;3;−4)⇒ Tọa độ điểm M thuộc đoạn IJ có dạng (1;1+3t;1−4t),t∈[0;1]
Mặt khác M∈(S) ⇒(1−1)2+(1−(1+3t))2+(1−(1−4t))2=1
⇔t2=125⇔[t=15t=−15(L)⇔t=15⇒M(1;85;15)⇒OM=3√105.
Hướng dẫn giải:
- Tìm tọa độ điểm I sao cho 3→IA+2→IB+→IC=→0.
- Biến đổi 3MA2+2MB2+MC2 qua dạng vecto và đánh giá giá trị nhỏ nhất của tổng.

