Các bài toán về đường thẳng và mặt cầu
Kỳ thi ĐGNL ĐHQG Hồ Chí Minh
Trong không gian Oxyz, cho điểm \(E\left( {2;1;3} \right)\), mặt phẳng \(\left( P \right):\,\,2x + 2y - z - 3 = 0\) và mặt cầu \(\left( S \right):\,\,{\left( {x - 3} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 5} \right)^2} = 36\). Gọi \(\Delta \) là đường thẳng đi qua E, nằm trong \(\left( P \right)\) và cắt \(\left( S \right)\) tại hai điểm có khoảng cách nhỏ nhất. Phương trình của \(\Delta \) là:
Dễ thấy \(E \in \left( P \right)\) . Gọi I\(\left( {3;2;5} \right)\) là tâm khối cầu.
Đường thẳng qua I vuông góc với (P): \(\left\{ \begin{array}{l}x = 3 + 2t\\y = 2 + 2t\\z = 5 - t\end{array} \right.\,\,\left( d \right)\).
Gọi H là hình chiếu của I lên (P) \( \Rightarrow H \in \left( d \right) \Rightarrow H\left( {3 + 2t;2 + 2t;5 - t} \right)\)
Lại có \(H \in \left( P \right)\)
\(\begin{array}{l} \Rightarrow 2\left( {3 + 2t} \right) + 2\left( {2 + 2t} \right) - 5 + t - 3 = 0\\ \Leftrightarrow 6 + 4t + 4 + 4t - 5 + t - 3 = 0\\ \Leftrightarrow 9t + 2 = 0 \Leftrightarrow t = \dfrac{{ - 2}}{9} \Rightarrow H\left( {\dfrac{{23}}{9};\dfrac{{14}}{9};\dfrac{{47}}{9}} \right)\\ \Rightarrow \overrightarrow {EH} \left( {\dfrac{5}{9};\dfrac{5}{9};\dfrac{{20}}{9}} \right) = \dfrac{5}{9}\left( {1;\;1;\;4} \right)//\left( {1;1;4} \right) = \overrightarrow a \end{array}\)
Để đường thẳng \(\left( \Delta \right)\) cắt mặt cầu (S) tại 2 điểm sao cho chúng có khoảng cách nhỏ nhất thì đường thẳng \(\left( \Delta \right)\) đi qua E và vuông góc với \(HE\).
Ta có: \(\left\{ \begin{array}{l}\overrightarrow {{u_\Delta }} \bot \overrightarrow {{n_P}} \\\overrightarrow {{u_\Delta }} \bot \overrightarrow a \end{array} \right. \Rightarrow \overrightarrow {{u_\Delta }} = \left[ {\overrightarrow {{n_P}} ;\overrightarrow a } \right] = \left( {\left| {\begin{array}{*{20}{c}}\begin{array}{l}2\\1\end{array}&\begin{array}{l} - 1\\4\end{array}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}\begin{array}{l} - 1\\4\end{array}&\begin{array}{l}2\\1\end{array}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}\begin{array}{l}2\\1\end{array}&\begin{array}{l}2\\1\end{array}\end{array}} \right|} \right) = \left( {9; - 9;\;0} \right) = 9\left( {1; - 1;0} \right)\).
Vậy đường thẳng \(\left( \Delta \right)\) đi qua E và nhận \(\left( {1; - 1;0} \right)\) là 1 VTCP.
Vậy phương trình đường thẳng \(\left( \Delta \right):\,\,\left\{ \begin{array}{l}x = 2 + t\\y = 1 - t\\z = 3\end{array} \right.\)
Trong không gian \(Oxyz\), cho điểm \(S\left( { - 2;1; - 2} \right)\) nằm trên mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} = 9\). Từ điểm \(S\) kẻ ba dây cung \(SA,SB,SC\) với mặt cầu \(\left( S \right)\) có độ dài bằng nhau và đôi một tạo với nhau góc \({60^0}\). Dây cung \(AB\) có độ dài bằng:
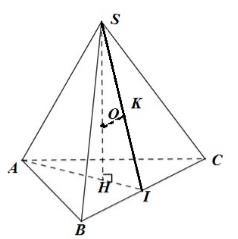
Xét tứ diện SABC có: \(SA = SB = SC\), \(\widehat {ASB} = \widehat {BSC} = \widehat {CSA} = {60^0}\)\( \Rightarrow SABC\) là tứ diện đều.
Mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} = 9\) có tâm O, bán kính \(R = 3\), ngoại tiếp khối tứ diện SABC \( \Rightarrow OS = OA = OB = OC = 3\)
Giả sử độ dài dây AB là a \( \Rightarrow \,SI = AI = \dfrac{{a\sqrt 3 }}{2}\)\( \Rightarrow \,AH = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\)
\( \Rightarrow SH = \sqrt {S{A^2} - A{H^2}} = \sqrt {{a^2} - \dfrac{1}{3}{a^2}} = \sqrt {\dfrac{2}{3}} a\)
\( \Rightarrow R = \dfrac{{{a^2}}}{{2\sqrt {\dfrac{2}{3}} a}} = \dfrac{{\sqrt 6 a}}{4} \Rightarrow \dfrac{{\sqrt 6 a}}{4} = 3 \Leftrightarrow a = 2\sqrt 6 \).
Trong không gian với hệ tọa độ \(Oxyz\), cho điểm \(I\left( {3;4; - {\mkern 1mu} 2} \right).\) Lập phương trình mặt cầu tâm \(I\) và tiếp xúc với trục \(Oz\).
Khoảng cách từ tâm \(I\) đến trục \(Oz\) là: \(d\left( {I;\left( {Oz} \right)} \right) = \sqrt {{3^2} + {4^2}} = 5.\)
Vì tiếp xúc với trục Oz nên bán kính mặt cầu R=5.
Vậy phương trình cần tìm là
\(\left( S \right):{\left( {x - 3} \right)^2} + {\left( {y - 4} \right)^2} + {\left( {z + 2} \right)^2} = 25.\)

