Giá trị lớn nhất, nhỏ nhất của hàm số
Kỳ thi ĐGNL ĐHQG Hồ Chí Minh
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = \sin x$ trên đoạn $\left[ { - \dfrac{\pi }{2}; - \dfrac{\pi }{3}} \right]$ lần lượt là
Ta có $y' = \cos x \Rightarrow y' = 0 \Leftrightarrow \cos x = 0 \Leftrightarrow x = \dfrac{\pi }{2} + k\pi \left( {k \in \mathbb{Z}} \right)$
Do $x\in \left[ { - \dfrac{\pi }{2}; - \dfrac{\pi }{3}} \right]$ nên $k=-1$ hay $x=-\dfrac{\pi }{2}$
Suy ra $y\left( { - \dfrac{\pi }{2}} \right) = - 1;\;\;y\left( { - \dfrac{\pi }{3}} \right) = - \dfrac{{\sqrt 3 }}{2} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{\rm{\;}}&{\mathop {\max}\limits_{\left[ { - \frac{\pi }{2}; - \frac{\pi }{3}} \right]}y = - \dfrac{{\sqrt 3 }}{2}}\\{{\rm{ \;}}}&{\mathop {\min }\limits_{\left[ { - \frac{\pi }{2}; - \frac{\pi }{3}} \right]} y = - 1}\end{array}} \right.$
Cho biết GTLN của hàm số $f\left( x \right)$ trên $\left[ {1;3} \right]$ là $M = - 2$. Chọn khẳng định đúng:
Nếu $M = - 2$ là GTLN của hàm số $y = f\left( x \right)$ trên $\left[ {1;3} \right]$ thì $f\left( x \right) \leqslant - 2,\forall x \in \left[ {1;3} \right]$.
Cho hàm số $f\left( x \right)$ xác định trên $\left[ {0;2} \right]$ và có GTNN trên đoạn đó bằng $5$. Chọn kết luận đúng:
GTNN của $f\left( x \right)$ trên $\left[ {0;2} \right]$ bằng $5$ nên $f\left( x \right) \geqslant 5,\forall x \in \left[ {0;2} \right] \Rightarrow f\left( 2 \right) \geqslant 5$.
Cho hàm số \(f\left( x \right)\) có bảng biến thiên như hình vẽ:
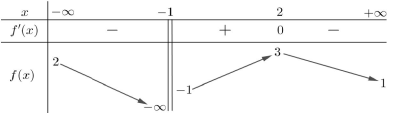
Tìm điều kiện của tham số \(m\) để \(m < f\left( x \right) + {x^2}\) với mọi \(x \in \left( {1;2} \right)\).
Đặt \(g\left( x \right) = f\left( x \right) + {x^2}\) ta có \(m < g\left( x \right)\,\,\forall x \in \left( {1;2} \right) \Leftrightarrow m \le \mathop {\min }\limits_{\left[ {1;2} \right]} g\left( x \right)\).
Ta có \(g'\left( x \right) = f'\left( x \right) + 2x\), với \(x \in \left( {1;2} \right)\)
Ta có \(\left\{ \begin{array}{l}f'\left( x \right) > 0\\2x > 0\end{array} \right. \Rightarrow g'\left( x \right) > 0\,\,\forall x \in \left( {1;2} \right)\).
\( \Rightarrow \) hàm số \(g\left( x \right)\) đồng biến trên \(\left( {1;2} \right)\).
\( \Rightarrow \mathop {\min }\limits_{\left[ {1;2} \right]} g\left( x \right) = g\left( 1 \right) = f\left( 1 \right) + 1\).
Vậy \(m \le f\left( 1 \right) + 1\).
Giá trị nhỏ nhất của hàm số $y = 2x + \cos x$ trên đoạn $\left[ {0;1} \right]$ là :
Ta có $y' = 2 - \sin x > 0{\mkern 1mu} {\mkern 1mu} \forall x \in R \Rightarrow $ Hàm số luôn đồng biến trên $\left[ {0;1} \right]$
$ \Rightarrow \mathop {\min }\limits_{\left[ {0;1} \right]} y = y\left( 0 \right) = 1$.
Cho hàm số $f\left( x \right)$ xác định và liên tục trên $R$, có $\mathop {\lim }\limits_{x \to + \infty } f(x) = + \infty ;\mathop {\lim }\limits_{x \to - \infty } f(x) = - \infty $ , khi đó:
Hàm số $y = f\left( x \right)$ có $\mathop {\lim }\limits_{x \to + \infty }f(x) = + \infty ;\mathop {\lim }\limits_{x \to - \infty } f(x) = - \infty $ thì không có GTLN, GTNN trên $R$ vì không tồn tại số $M,m$ để $f\left( x \right) \leqslant M,f\left( x \right) \geqslant m,\forall x \in R$.
Gọi $m$ là giá trị nhỏ nhất của hàm số $y = x - 1 + \dfrac{4}{{x - 1}}$ trên khoảng $\left( {1; + \infty {\rm{\;}}} \right)$. Tìm $m?$
${\rm{\;}}x > 1 \Leftrightarrow x - 1 > 0$
$ \Rightarrow y = x - 1 + \dfrac{4}{{x - 1}} \ge 2\sqrt {\left( {x - 1} \right).\dfrac{4}{{x - 1}}} = 2.2 = 4$
Dấu bằng xảy ra $ \Leftrightarrow x - 1 = \dfrac{4}{{x - 1}} \Leftrightarrow {\left( {x - 1} \right)^2} = 4 \Leftrightarrow x = 3$.
Vậy GTNN của hàm số là $m=4$ khi $x=3$.
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như hình vẽ, chọn kết luận đúng:
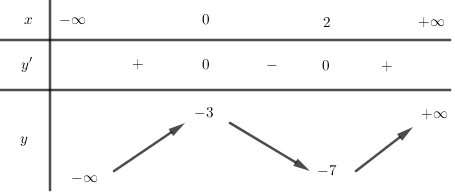
Ta có:
+) $\mathop {\max }\limits_{\left[ { - 3;0} \right]} f\left( x \right) = f\left( 0 \right) = - 3$ nên A sai.
+) $\mathop {\min }\limits_{\left[ {1;3} \right]} f\left( x \right) = f\left( 2 \right) = - 7$ nên B đúng.
+) Vì $\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = - \infty $ nên không tồn tại $\mathop {\min}\limits_{\left( { - \infty ;2} \right]} f\left( x \right)$ nên C sai.
+) $\mathop {\max }\limits_{\left[ { - 1;1} \right]} f\left( x \right) = f\left( 0 \right) = - 3$ nên D sai.
Cho hàm số $y = f\left( x \right)$ có đồ thị như hình vẽ. Khẳng định nào sau đây là đúng?
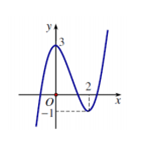
A sai vì $y=3$ là giá trị cực đại của hàm số, không phải giá trị lớn nhất.
B sai vì hàm số đồng biến trên các khoảng $\left( { - \infty ;0} \right),\left( {2; + \infty } \right)$.
C sai vì $x=2$ là điểm cực tiểu của hàm số không phải giá trị cực tiểu.
D đúng vì trên đoạn $\left[ {0;4} \right]$ thì hàm số đạt GTNN (cũng là giá trị cực tiểu) bằng $ - 1$ đạt được tại $x = 2$.
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau:
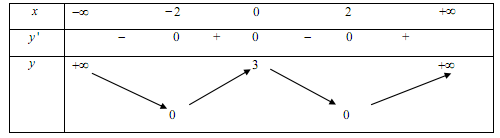
Khẳng định nào sau đây là khẳng định đúng?
Đáp án A: Hàm số đạt cực đại tại $x = 0$ và $y = 3$ là giá trị cực đại của hàm số nên A sai.
Đáp án B: GTNN và giá trị cực tiểu của hàm số là $y = 0$ nên B đúng và C sai.
Đáp án D: Hàm số không có GTLN vì $\mathop {\lim }\limits_{x \to \pm \infty } y = + \infty $.
Tìm giá trị lớn nhất của hàm số $y = {x^3} - 5{{\text{x}}^2} + 3{\text{x}} - 1$ trên đoạn $\left[ {2;4} \right]$
$y' = 3{x^2} - 10x + 3 = 0 \Leftrightarrow \left[ \begin{gathered}x = 3 \in \left[ {2;4} \right] \hfill \\x = \dfrac{1}{3} \notin \left[ {2;4} \right] \hfill \\ \end{gathered} \right.$
$f\left( 2 \right) = - 7,f\left( 3 \right) = - 10,f\left( 4 \right) = - 5$
Vậy giá trị lớn nhất của hàm số $y = {x^3} - 5{{\text{x}}^2} + 3{\text{x}} - 1$ trên đoạn $\left[ {2;4} \right]$ là $M = - 5$
Tìm GTLN và GTNN của hàm số $y = {x^5} - 5{x^4} + 5{x^3} + 1$ trên đoạn $\left[ { - 1;2} \right]$
Ta có: $y' = 5{{\text{x}}^4} - 20{{\text{x}}^3} + 15{{\text{x}}^2} = 0 \Leftrightarrow 5{x^2}\left( {{x^2} - 4x + 3} \right) = 0 \Leftrightarrow \left[ \begin{gathered}x = 0 \in \left[ { - 1;2} \right] \hfill \\x = 1 \in \left[ { - 1;2} \right] \hfill \\x = 3 \notin \left[ { - 1;2} \right] \hfill \\ \end{gathered} \right.$
$f( - 1) = - 10, f(0) = 1,$ $ f(1) = 2, f(2) = - 7$
Vậy giá trị lớn nhất, nhỏ nhất của hàm trên $\left[ { - 1;2} \right]$ lần lượt là $2$ và $ - 10$
Giá trị lớn nhất của hàm số $f\left( {\text{x}} \right) = \dfrac{{6 - 8{\text{x}}}}{{{x^2} + 1}}$ trên tập xác định của nó là:
TXĐ: $D=R$
Ta có: $f'\left( x \right) = \dfrac{{8{{\text{x}}^2} - 12{\text{x}} - 8}}{{{{\left( {{x^2} + 1} \right)}^2}}}$
$f'\left( x \right) = 0 \Leftrightarrow x = 2$ hoặc $x = - \dfrac{1}{2}$
$\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to - \infty } y = 0$
Bảng biến thiên
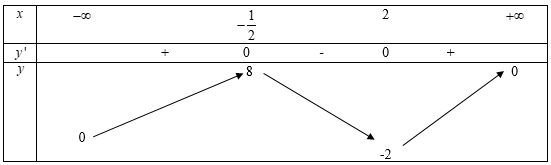
Vậy giá trị lớn nhất của hàm số là $y = 8$ tại $x = - \dfrac{1}{2}$
Gọi giá trị lớn nhất và nhỏ nhất của hàm số $y = {x^4} + 2{x^2} - 1$ trên đoạn $\left[ { - 1;2} \right]$ lần lượt là $M$ và $m$. Khi đó giá trị của $M.m$ là:
TXĐ: $D=R$
Ta có: $y' = 4{{\text{x}}^3} + 4{\text{x}}$$ \Rightarrow y' = 0 \Leftrightarrow x = 0 \in \left[ { - 1;2} \right]$
$f( - 1) = 2,{\text{ f(0) = }} - 1,{\text{ f(2) = 23}}$
Ta thấy GTLN và GTNN lần lượt là $M = 23,m = - 1 \Rightarrow M.m = 23.\left( { - 1} \right) = - 23$
Cho hàm số $y = x + \dfrac{1}{x}.$ Giá trị nhỏ nhất của hàm số trên khoảng $\left( {0;\, + \infty } \right)$ là:
TXĐ: \(R\backslash \left\{ 0 \right\}\)
$y' = 1 - \dfrac{1}{{{x^2}}} = \dfrac{{{x^2} - 1}}{{{x^2}}}$
$y' = 0 \Leftrightarrow \dfrac{{{x^2} - 1}}{{{x^2}}} = 0 \Leftrightarrow {x^2} - 1 = 0 \Leftrightarrow x=1 (tm) $ hoặc $x=-1 (ktm)$
Bảng biến thiên:
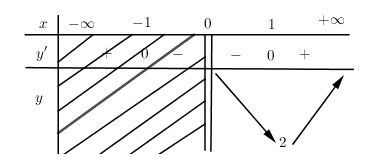
$ \Rightarrow \mathop {Min}\limits_{x \in \left( {0; + \infty } \right)} \,y = f\left( 1 \right) = 2$
Cho hàm số $y = \dfrac{{2mx + 1}}{{m - x}}.$ Giá trị lớn nhất của hàm số trên $\left[ {2;3} \right]$ bằng $\dfrac{{ - 1}}{3}$ khi m bằng:
\(D = \mathbb{R}\backslash \left\{ m \right\}{\rm{ }} \Rightarrow {\rm{m}} \notin \left[ {2;3} \right]\)
\(\begin{array}{l}y = \dfrac{{2mx + 1}}{{ - x + m}}\\ \Rightarrow y' = \dfrac{{2m\left( { - x + m} \right) + 1.\left( {2mx + 1} \right)}}{{{{\left( { - x + m} \right)}^2}}} = \dfrac{{2{m^2} + 1}}{{{{\left( { - x + m} \right)}^2}}} > 0\,,\forall x \in \left[ {2;3} \right]\end{array}\)
Hàm số luôn đồng biến trên \(\left[ {2;3} \right]\)
\(\begin{array}{l} \Rightarrow Max\,y = f\left( 3 \right) = \dfrac{{6m + 1}}{{m - 3}}\\Max\,y = \dfrac{{ - 1}}{3} \Leftrightarrow \dfrac{{6m + 1}}{{m - 3}} = \dfrac{{ - 1}}{3} \Leftrightarrow 18m + 3 = - m + 3 \Leftrightarrow 19m = 0 \Leftrightarrow m = 0(TMDK)\end{array}\)
Cho hàm số $y = {x^3} - 3m{x^2} + 6$, giá trị nhỏ nhất của hàm số trên $\left[ {0;3} \right]$ bằng $2$ khi:
TXĐ: $D = \mathbb{R}$
$y' = 3{x^2} - 6mx.$
Ta có: $y' = 0 \Leftrightarrow \left[ \begin{gathered}x = 0 \Rightarrow y = 6 \hfill \\x = 2m \Rightarrow y = - 4{m^3} + 6 \hfill \\ \end{gathered} \right.$
$y^{\prime}=0 \Leftrightarrow\left[\begin{array}{c}x=0 \Rightarrow y=6 \\ x=2 m \Rightarrow y=-4 m^{3}+6\end{array}\right.$
Xét TH1: $m = 0$. Hàm số đồng biến trên $\left[ {0;3} \right]$ $ \Rightarrow \mathop {Min}\limits_{\left[ {0;3} \right]} y = y\left( 0 \right) = 6 \Rightarrow $ loại.
Xét TH2: $m \geqslant \dfrac{3}{2} \Rightarrow 2m \ge 3 > 0$. Khi đó, hàm số nghịch biến trên $\left[ {0;3} \right] \subset \left[ {0;2m} \right]$
$ \Rightarrow \mathop {Min}\limits_{\left[ {0;3} \right]} y = y\left( 3 \right) = 33 - 27m = 2 \Rightarrow m = \dfrac{{31}}{{27}} < \dfrac{3}{2}$(loại)
Xét TH3: $\dfrac{3}{2} > m > 0 \Rightarrow 3 > 2m > 0$
Bảng biến thiên:
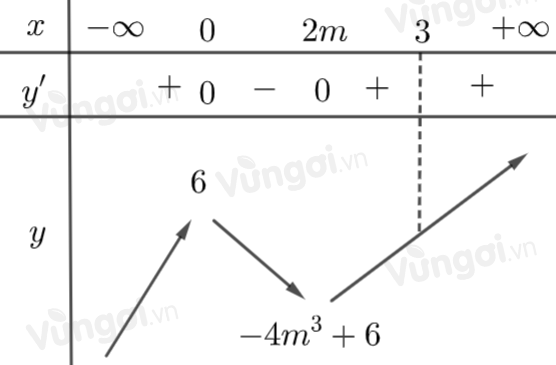
=> Đồ thị hàm số có điểm cực đại là $\left( {0;6} \right)$ và điểm cực tiểu là $\left( {2m, - 4{m^3} + 6} \right).$
Khi đó , GTNN trên $\left[ {0;3} \right]$ là $y\left( {2m} \right) = - 4{m^3} + 6$ $ \Rightarrow - 4{m^3} + 6 = 2 \Leftrightarrow {m^3} = 1 \Leftrightarrow m = 1$ (thỏa mãn)
Xét TH4: $m < 0 \Rightarrow \left( {0;6} \right)$ là điểm cực tiểu của đồ thị hàm số và trên $\left[ {0;3} \right]$ hàm số đồng biến.
$ \Rightarrow {y_{min}} = 6 \Rightarrow $ loại.
Vậy $m = 1$ là giá trị cần tìm.
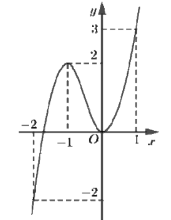
Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên \(\mathbb{R}\), có đồ thị như hình vẽ bên. Tìm giá trị nhỏ nhất \(m\) và giá trị lớn nhất \(M\) của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ { - 2;2} \right]\).
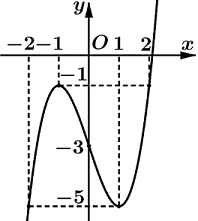
Dựa vào đồ thị hàm số ta có: \(\left\{ \begin{array}{l}m = \mathop {\min }\limits_{\left[ { - 2;2} \right]} f\left( x \right) = - 5\\M = \mathop {{\rm{max}}}\limits_{\left[ { - 2;2} \right]} f\left( x \right) = - 1\end{array} \right.\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình dưới. Gọi \(a,\,\,A\) lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của \(f\left( {x + 1} \right)\) trên đoạn \(\left[ { - 1;\,\,0} \right].\) Giá trị \(a + A\) bằng:
Đặt \(x + 1 = t.\) Khi đó: \(x \in \left[ { - 1;\,\,0} \right] \Rightarrow t \in \left[ {0;\,\,1} \right].\)
Dựa vào đồ thị hàm số ta thấy: \(\left\{ \begin{array}{l}a = \mathop {Min}\limits_{\left[ {0;\,1} \right]} f\left( t \right) = 0\,\,\,khi\,\,\,t = 0 \Rightarrow x = - 1.\\A = \mathop {Max}\limits_{\left[ {0;\,1} \right]} f\left( t \right) = 3\,\,\,\,khi\,\,\,t = 1 \Rightarrow x = 0.\end{array} \right.\)
\( \Rightarrow a + A = 0 + 3 = 3.\)
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;4} \right]\) và có đồ thị như hình vẽ
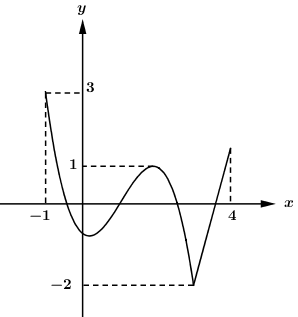
Có tất cả bao nhiêu giá trị nguyên của m thuộc đoạn \(\left[ { - 10;10} \right]\) để bất phương trình \(\left| {f\left( x \right) + m} \right| < 2m\) đúng với mọi x thuộc đoạn \(\left[ { - 1;4} \right]\)?
Ta có: \(\left| {f\left( x \right) + m} \right| < 2m\)
\(\Leftrightarrow - 2m < f\left( x \right) + m < 2m\)
\(\Leftrightarrow - 3m < f\left( x \right) < m\)
\( \Leftrightarrow \left\{ \begin{array}{l} - 3m < \mathop {\min }\limits_{\left[ { - 1;4} \right]} f\left( x \right)\\\mathop {\max }\limits_{\left[ { - 1;4} \right]} f\left( x \right) < m\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 3m < - 2\\3 < m\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > \dfrac{2}{3}\\m > 3\end{array} \right. \Leftrightarrow m > 3\).
Kết hợp điều kiện đề bài \( \Rightarrow m \in \left( {3;10} \right],\,\,m \in \mathbb{Z} \Rightarrow m \in \left\{ {4;5;6;7;8;9;10} \right\}\).
Vậy có 7 giá trị của m thỏa mãn yêu cầu bài toán.

