Giá trị lớn nhất, nhỏ nhất của hàm số
Kỳ thi ĐGNL ĐHQG Hồ Chí Minh
Gọi \(M,\,\,N\) lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(f\left( x \right) = \left| {x - 3} \right|\sqrt {x + 1} \) trên đoạn \(\left[ {0;4} \right]\). Tính\(M + 2N\).
Hàm số xác định trên \(\left[ {0;4} \right]\).
Ta có: \(f\left( x \right) = \left| {x - 3} \right|\sqrt {x + 1} = \sqrt {\left( {x + 1} \right){{\left( {x - 3} \right)}^2}} \).
Xét hàm số \(g\left( x \right) = \left( {x + 1} \right){\left( {x - 3} \right)^2}\) trên đoạn \(\left[ {0;4} \right]\) ta có:
\(\begin{array}{l}g'\left( x \right) = {\left( {x - 3} \right)^2} + \left( {x + 1} \right).2\left( {x - 3} \right)\\g'\left( x \right) = \left( {x - 3} \right)\left( {x - 3 + 2x + 2} \right)\\g'\left( x \right) = \left( {x - 3} \right)\left( {3x - 1} \right)\\g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 3 \in \left[ {0;4} \right]\\x = \dfrac{1}{3} \in \left[ {0;4} \right]\end{array} \right.\end{array}\)
Ta có: \(g\left( 0 \right) = 9,\,\,g\left( {\dfrac{1}{3}} \right) = \dfrac{{256}}{{27}},\,\,g\left( 3 \right) = 0,\,\,g\left( 4 \right) = 5\).
Vậy \(\left\{ \begin{array}{l}M = \mathop {\max }\limits_{\left[ {0;4} \right]} f\left( x \right) = \sqrt {g\left( {\dfrac{1}{3}} \right)} = \dfrac{{16\sqrt 3 }}{9}\\N = \mathop {\min }\limits_{\left[ {0;4} \right]} f\left( x \right) = \sqrt {g\left( 0 \right)} = 0\end{array} \right.\)\( \Rightarrow M + 2N = \dfrac{{16\sqrt 3 }}{9}\).
Một sợi dây kim loại dài \(a\,\,\left( {{\rm{cm}}} \right)\) . Người ta cắt sợi dây đó thành hai đoạn, trong đó một đoạn có độ dài \(x\,\,\left( {{\rm{cm}}} \right)\) được uốn thành đường tròn và đoạn còn lại được uốn thành hình vuông \(\left( {a > x > 0} \right).\) Tìm \(x\) để hình vuông và hình tròn tương ứng có tổng diện tích nhỏ nhất.
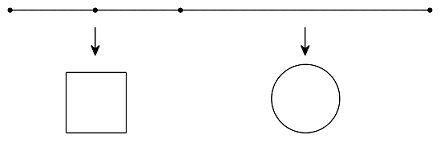
Do \(x\) là độ dài của đoạn dây cuộn thành hình tròn \(\left( {0 < x < a} \right)\). Suy ra chiều dài đoạn còn lại là \(a - x\).
Gọi \(r\) là bán kính của đường tròn. Chu vi đường tròn: \(2\pi r = x\)\( \Rightarrow r = \dfrac{x}{{2\pi }}\).
Do đó diện tích hình tròn là: \({S_1} = \pi .{r^2}\)\( = \dfrac{{{x^{\rm{2}}}}}{{4\pi }}\).
Chu vi hình vuông là \(a - x \Rightarrow \) Cạnh hình vuông là \(\dfrac{{a - x}}{4}\). Do đó diện tích hình vuông: \({S_2} = {\left( {\dfrac{{a - x}}{4}} \right)^2}\).
Tổng diện tích hai hình:
\(\begin{array}{l}S = \dfrac{{{x^2}}}{{4\pi }} + {\left( {\dfrac{{a - x}}{4}} \right)^2}\\\,\,\,\, = \dfrac{{4{x^2} + \pi {{\left( {a - x} \right)}^2}}}{{16\pi }}\\\,\,\,\,\, = \dfrac{{\left( {4 + \pi } \right).{x^2} - 2a\pi x + \pi {a^2}}}{{16\pi }}\end{array}\)
Xét hàm số \(S\left( x \right) = \dfrac{{\left( {4 + \pi } \right).{x^2} - 2a\pi x + \pi {a^2}}}{{16\pi }}\) ta có:\(S'\left( x \right) = \dfrac{{2\left( {4 + \pi } \right).x - 2a\pi }}{{16\pi }} = \dfrac{{\left( {4 + \pi } \right).x - a\pi }}{{8\pi }}\).
Cho\(S'\left( x \right) = 0 \Leftrightarrow \left( {4 + \pi } \right)x - a\pi = 0 \Leftrightarrow x = \dfrac{{a\pi }}{{4 + \pi }}\). Ta có BBT như sau :
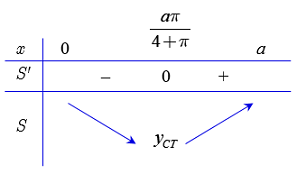
Suy ra hàm \(S\) chỉ có một cực trị và là cực tiểu tại \(x = \dfrac{{a\pi }}{{4 + \pi }}\).
Do đó \(S\) đạt giá trị nhỏ nhất tại \(x = \dfrac{{a\pi }}{{4 + \pi }}\).
Gọi \(M\) và \(m\) là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = 2{\sin ^2}x - \cos x + 1\). Khi đó, giá trị của tổng \(M + m\) bằng:
\(\begin{array}{l}\,\,\,\,\,\,\,y = 2{\sin ^2}x - \cos x + 1\\ \Rightarrow y = 2\left( {1 - {{\cos }^2}x} \right) - \cos x + 1\\ \Rightarrow y = - 2{\cos ^2}x - \cos x + 3\end{array}\)
Đặt \(\cos x = t\,\,\,\,\left( { - 1 \le t \le 1} \right)\), hàm số trở thành: \(y = - 2{t^2} - t + 3.\)
Ta có: \(y' = - 4t - 1 = 0 \Rightarrow t = - \dfrac{1}{4}\,\,\,\left( {tm} \right)\).
Bảng biến thiên:
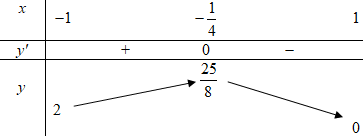
Từ BBT ta suy ra \(M = \dfrac{{25}}{8},\,\,m = 0\).
Vậy \(M + m = \dfrac{{25}}{8}\).
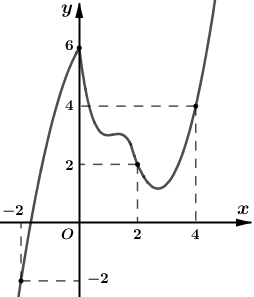
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) có đồ thị \(y = f'\left( x \right)\) như hình vẽ. Đặt \(g\left( x \right) = 2f\left( x \right) - {x^2}\). Khi đó giá trị lớn nhất của hàm số \(g\left( x \right)\) trên đoạn \(\left[ { - 2;4} \right]\) là:
Ta có \(g\left( x \right) = 2f\left( x \right) - {x^2}\) \( \Rightarrow g'\left( x \right) = 2f'\left( x \right) - 2x\)
Cho \(g'\left( x \right) = 0 \Leftrightarrow f'\left( x \right) = x\,\,\,\left( 1 \right)\).
Nghiệm của phương trình (1) là hoành độ giao điểm của hai đồ thị hàm số \(y = f'\left( x \right);\,\,y = x.\)
Vẽ đường thẳng \(y = x\) và đồ thị hàm số \(y = f'\left( x \right)\) trên cùng hệ trục tọa độ:
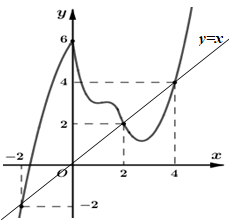
Dựa vào đồ thị ta thấy đồ thị hai hàm số \(y = f'\left( x \right);\,\,y = x\) cắt nhau tại 3 điểm có hoành độ là \( - 2;2;4.\)
\( \Rightarrow g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 2\\x = 2\\x = 4\end{array} \right.\)
Bảng biến thiên đồ thị hàm số \(y = g\left( x \right)\):
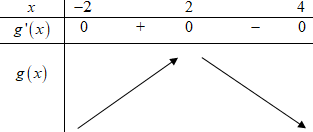
Dựa vào bảng biến thiên ta thấy giá trị lớn nhất của hàm số \(g\left( x \right)\) trên đoạn \(\left[ { - 2;4} \right]\) là \(g\left( 2 \right)\).
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) và có đồ thị như hình vẽ bên. Xét hàm số \(g\left( x \right) = f\left( {{x^3} + 2x} \right) + m\). Giá trị của tham số \(m\) để giá trị lớn nhất của hàm số \(g\left( x \right)\) trên đoạn \(\left[ {0;1} \right]\) bằng \(9\) là:
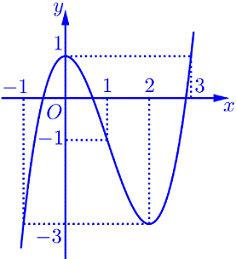
Ta có : \(g'\left( x \right) = \left( {3{x^2} + 2} \right).f'\left( {{x^3} + 2x} \right)\)
\(g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}3{x^2} + 2 = 0\\f'\left( {{x^3} + 2x} \right) = 0\end{array} \right. \Leftrightarrow f'\left( {{x^3} + 2x} \right) = 0\) (Do phương trình \(3{x^2} + 2 = 0\) vô nghiệm).
Từ đồ thị hàm số \(f\left( x \right)\) đã cho ta có : \(f'\left( {{x^3} + 2x} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}{x^3} + 2x = 0\\{x^3} + 2x = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = {x_0} \approx 0,77\end{array} \right.\)
Hàm số \(g\left( x \right)\) trên đoạn \(\left[ {0;1} \right]\) có :
\(\begin{array}{l}g\left( 0 \right) = f\left( 0 \right) + m = m + 1\\g\left( {{x_0}} \right) = f\left( 2 \right) + m = m - 3\\g\left( 1 \right) = f\left( 3 \right) + m = m + 1\end{array}\)
Do đó, \(\mathop {\max }\limits_{\left[ {0;1} \right]} g\left( x \right) = g\left( 0 \right) = g\left( 1 \right) = m + 1\).
Theo giả thiết, giá trị lớn nhất của hàm số \(g\left( x \right)\) trên \(\left[ {0;1} \right]\) bằng 9 nên \(m + 1 = 9 \Leftrightarrow m = 8\).
Vậy \(m = 8.\)
Hàm số nào dưới đây có giá trị nhỏ nhất trên tập xác định?
Các hàm số đã cho đều có TXĐ:\(D = \mathbb{R}\)
Ta có:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to - \infty } \left( {{x^3} - 3x + 2} \right) = - \infty \\\mathop {\lim }\limits_{x \to + \infty } \left( { - 2{x^3} + 3{x^2} - 1} \right) = - \infty \\\mathop {\lim }\limits_{x \to \pm \infty } \left( {{x^4} - 2{x^2} - 1} \right) = + \infty \\\mathop {\lim }\limits_{x \to \pm \infty } \left( { - {x^4} + 4{x^2}} \right) = - \infty \end{array}\)
Do đó, hàm số có giá trị nhỏ nhất trên tập xác định là \(y = {x^4} - 2{x^2} - 1\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ. Gọi \(M\) và \(m\) tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = f\left( {1 - 2\cos x} \right)\) trên \(\left[ {0;\,\,\dfrac{{3\pi }}{2}} \right]\). Giá trị của \(M + m\) bằng
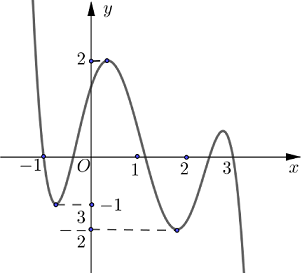
Đặt \(t = 1 - 2\cos x\). Với \(x \in \left[ {0;\,\,\dfrac{{3\pi }}{2}} \right]\) thì \(\cos x \in \left[ { - 1;1} \right] \Rightarrow \)\(1 - 2\cos x \in \left[ { - 1;3} \right] \Rightarrow t \in \left[ { - 1;3} \right].\)
Khi đó ta có \(y = f\left( t \right)\) với \(t \in \left[ { - 1;3} \right]\).
Quan sát đồ thị hàm số \(y = f\left( t \right)\) trên đoạn \(\left[ { - 1;3} \right]\), ta thấy GTLN của hàm số là 2, GTNN của hàm số là \( - \dfrac{3}{2}\)
\( \Rightarrow M = 2,\,\,m = - \dfrac{3}{2} \Rightarrow M + m = \dfrac{1}{2}\)
Cho các số thực $x, y$ thỏa mãn ${\left( {x - 4} \right)^2} + {\left( {y - 4} \right)^2} + 2xy \leqslant 32.$ Giá trị nhỏ nhất $m$ của biểu thức $A = {x^3} + {y^3} + 3\left( {xy - 1} \right)\left( {x + y - 2} \right)$ là:
${\left( {x - 4} \right)^2} + {\left( {y - 4} \right)^2} + 2xy \leqslant 32 $ $\Leftrightarrow {\left( {x + y} \right)^2} - 8\left( {x + y} \right) \leqslant 0 $ $\Leftrightarrow 0 \leqslant x + y \leqslant 8$
$A = {\left( {x + y} \right)^3} - 3\left( {x + y} \right) - 6xy + 6 $ $\geqslant {\left( {x + y} \right)^3} - \dfrac{3}{2}{\left( {x + y} \right)^2} - 3\left( {x + y} \right) + 6$
(do ${\left( {x + y} \right)^2} \geqslant 4xy $ $\Rightarrow xy \leqslant \dfrac{{{{\left( {x + y} \right)}^2}}}{4} $ $\Rightarrow - 6xy \geqslant - \dfrac{3}{2}{\left( {x + y} \right)^2}$ )
Xét hàm số $f\left( t \right) = {t^3} - \dfrac{3}{2}{t^2} - 3t + 6$ trên đoạn $\left[ {0,8} \right]$, ta có
$f'\left( t \right) = 3{t^2} - 3t - 3,f'\left( t \right) = 0 $ $\Leftrightarrow t = \dfrac{{1 \pm \sqrt 5 }}{2}$
(giá trị $\dfrac{{1 - \sqrt 5 }}{2} \notin \left[ {0;8} \right]$ nên loại)
Thực hiện tính toán ta có: $f\left( 0 \right) = 6,f\left( {\dfrac{{1 + \sqrt 5 }}{2}} \right) = \dfrac{{17 - 5\sqrt 5 }}{4},f\left( 8 \right) = 398 $
$\Rightarrow A \geqslant f\left( t \right) \geqslant \dfrac{{17 - 5\sqrt 5 }}{4} \Rightarrow A \geqslant \dfrac{{17 - 5\sqrt 5 }}{4}$
Vậy giá trị nhỏ nhất của $A$ là $\dfrac{{17 - 5\sqrt 5 }}{4}$ xảy ra khi $\left\{ \begin{gathered} x + y = \dfrac{{1 + \sqrt 5 }}{2} \hfill \\ x = y \hfill \\ \end{gathered} \right. \Leftrightarrow x = y = \dfrac{{1 + \sqrt 5 }}{4}$
Có bao nhiêu số nguyên \(m \in \left[ { - 5;5} \right]\) để \(\mathop {\min }\limits_{\left[ {1;3} \right]} \left| {{x^3} - 3{x^2} + m} \right| \ge 2\).
Xét hàm số \(y = f\left( x \right) = {x^3} - 3{x^2} + m\) trên \(\left[ {1;3} \right]\), có \(f'\left( x \right) = 3{x^2} - 6x,\,\,f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\,\left( L \right)\\x = 2\end{array} \right.\)
Bảng biến thiên:
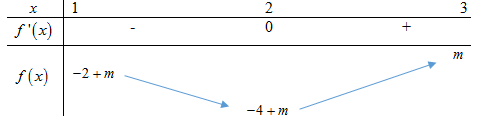
\(\mathop {\min }\limits_{\left[ {1;3} \right]} \left| {{x^3} - 3{x^2} + m} \right| \ge 2 \Rightarrow \left[ \begin{array}{l}m - 4 > 0\\m < 0\end{array} \right.\)
TH1: \(m - 4 > 0 \Leftrightarrow m > 4\)
\(\mathop {\min }\limits_{\left[ {1;3} \right]} \left| {{x^3} - 3{x^2} + m} \right| \ge 2 \Leftrightarrow m - 4 \ge 2 \Leftrightarrow m \ge 6\)
Mà \(m \in \left[ { - 5;5} \right] \Rightarrow m \in \emptyset \)
TH2: \(m < 0\)
\(\mathop {\min }\limits_{\left[ {1;3} \right]} \left| {{x^3} - 3{x^2} + m} \right| \ge 2 \Leftrightarrow - m \ge 2 \Leftrightarrow m \le - 2\)
Mà \(m \in \left[ { - 5;5} \right],m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 5; - 4; - 3; - 2} \right\}\): 4 giá trị.
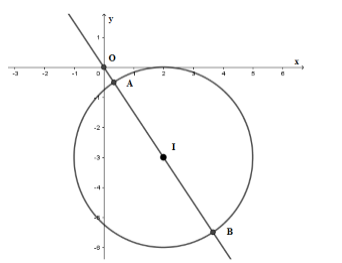
Cho hai số thực \(x,\,y\) thỏa mãn \({x^2} + {y^2} - 4x + 6y + 4 + \sqrt {{y^2} + 6y + 10} = \sqrt {6 + 4x - {x^2}} \). Gọi \(M,\,m\) lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức \(T = \left| {\sqrt {{x^2} + {y^2}} - a} \right|\). Có bao nhiêu giá trị nguyên thuộc đoạn \(\left[ { - 10;\,10} \right]\) của tham số \(a\) để \(M \ge 2m\)?
Ta có \({x^2} + {y^2} - 4x + 6y + 4 + \sqrt {{y^2} + 6y + 10} = \sqrt {6 + 4x - {x^2}} \)
\(\begin{array}{l} \Leftrightarrow {x^2} + {y^2} - 4x + 6y + 4 + \sqrt {{y^2} + 6y + 10} - \sqrt {6 + 4x - {x^2}} = 0\\ \Leftrightarrow {x^2} + {y^2} - 4x + 6y + 4 + \dfrac{{\left( {\sqrt {{y^2} + 6y + 10} - \sqrt {6 + 4x - {x^2}} } \right)\left( {\sqrt {{y^2} + 6y + 10} + \sqrt {6 + 4x - {x^2}} } \right)}}{{\sqrt {{y^2} + 6y + 10} + \sqrt {6 + 4x - {x^2}} }} = 0\end{array}\)
\(\begin{array}{l} \Leftrightarrow {x^2} + {y^2} - 4x + 6y + 4 + \dfrac{{{y^2} + 6y + 10 - 6 - 4x + {x^2}}}{{\sqrt {{y^2} + 6y + 10} + \sqrt {6 + 4x - {x^2}} }} = 0\\ \Leftrightarrow {x^2} + {y^2} - 4x + 6y + 4 + \dfrac{{{x^2} + {y^2} - 4x + 6y + 4}}{{\sqrt {{y^2} + 6y + 10} + \sqrt {6 + 4x - {x^2}} }} = 0\end{array}\)
\( \Leftrightarrow \left( {{x^2} + {y^2} - 4x + 6y + 4} \right)\left( {1 + \dfrac{1}{{\sqrt {{y^2} + 6y + 10} + \sqrt {6 + 4x - {x^2}} }}} \right) = 0\)
\( \Leftrightarrow {x^2} + {y^2} - 4x + 6y + 4 = 0\) (vì \(1 + \dfrac{1}{{\sqrt {{y^2} + 6y + 10} + \sqrt {6 + 4x - {x^2}} }} > 0\) )
\( \Leftrightarrow {\left( {x - 2} \right)^2} + {\left( {y + 3} \right)^2} = 9\)
Phương trình \({\left( {x - 2} \right)^2} + {\left( {y + 3} \right)^2} = 9\) là phương trình đường tròn \(\left( C \right)\) tâm \(I\left( {2; - 3} \right)\) và bán kính \(R = 3.\)
Gọi \(N\left( {x;y} \right) \in \left( C \right)\) ta suy ra \(ON = \sqrt {{x^2} + {y^2}} \) suy ra \(T = \left| {ON - a} \right|\)
Gọi \(A,B\) là giao điểm của đường tròn \(\left( C \right)\) và đường thẳng \(OI\).
Khi đó \(OA = OI - R = \sqrt {13} - 3\) và \(OB = OI + R = \sqrt {13} + 3\)
Suy ra \(\sqrt {13} - 3 \le \sqrt {{x^2} + {y^2}} \le \sqrt {13} + 3\)
TH1: Nếu \(\sqrt {13} - 3 \le a \le \sqrt {13} + 3\) thì \(\left| {\sqrt {{x^2} + {y^2}} - a} \right| \ge 0 \Rightarrow \min T = 0 \Rightarrow M \ge 2m \Rightarrow a \in \left\{ {1;2;3;4;5;6} \right\}\)
TH2: Nếu \(a < \sqrt {13} - 3 \Rightarrow a < \sqrt {13} \) nên \(\left| {\sqrt {13} + 3 - a} \right| > \left| {\sqrt {13} - 3 - a} \right|\), do đó \(M = \left| {\sqrt {13} + 3 - a} \right|;m = \left| {\sqrt {13} - 3 - a} \right|\)
Vì \(M \ge 2m \Rightarrow \left| {\sqrt {13} + 3 - a} \right| \ge 2\left| {\sqrt {13} - 3 - a} \right|\)
\( \Leftrightarrow {\left( {\sqrt {13} + 3 - a} \right)^2} - {\left( {2\sqrt {13} - 6 - 2a} \right)^2} \ge 0 \Leftrightarrow \sqrt {13} - 9 \le a \le \sqrt {13} - 1 \Rightarrow a \in \left\{ { - 5; - 4; - 3; - 2; - 1;0} \right\}\)
TH3: Nếu \(a > \sqrt {13} + 3 \Rightarrow a > \sqrt {13} \) nên \(\left| {\sqrt {13} + 3 - a} \right| < \left| {\sqrt {13} - 3 - a} \right|\), do đó \(m = \left| {\sqrt {13} + 3 - a} \right|;M = \left| {\sqrt {13} - 3 - a} \right|\)
Vì \(M \ge 2m \Rightarrow \left| {\sqrt {13} - 3 - a} \right| \ge 2\left| {\sqrt {13} + 3 - a} \right|\)
\( \Leftrightarrow {\left( {\sqrt {13} - 3 - a} \right)^2} - {\left( {2\sqrt {13} + 6 - 2a} \right)^2} \ge 0 \Leftrightarrow \sqrt {13} + 1 \le a \le \sqrt {13} + 9 \Rightarrow a \in \left\{ {7;8;9;10} \right\}\)
Vậy có 16 giá trị của \(a\) thỏa mãn đề bài.
Cho \(f\left( x \right)\) mà đồ thị hàm số \(y = f'\left( x \right)\) như hình vẽ bên
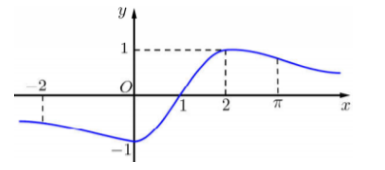
Bất phương trình \(f\left( x \right) > \sin \dfrac{{\pi x}}{2} + m\) nghiệm đúng với mọi \(x \in \left[ { - 1;3} \right]\) khi và chỉ khi:
\(\begin{array}{l}f\left( x \right) > \sin \dfrac{{\pi x}}{2} + m\,\,\forall x \in \left[ { - 1;3} \right] \Leftrightarrow g\left( x \right) = f\left( x \right) - \sin \dfrac{{\pi x}}{2} > m\,\,\forall x \in \left[ { - 1;3} \right]\\ \Rightarrow m < \mathop {\min }\limits_{\left[ { - 1;3} \right]} g\left( x \right)\end{array}\).
Từ đồ thị hàm số \(y = f'\left( x \right)\) ta suy ra BBT đồ thị hàm số \(y = f\left( x \right)\) như sau:
Dựa vào BBT ta thấy \(f\left( x \right) \ge f\left( 1 \right)\,\,\forall x \in \left[ { - 1;3} \right]\).
\(\begin{array}{l}x \in \left[ { - 1;3} \right] \Rightarrow \dfrac{{\pi x}}{2} \in \left[ { - \dfrac{\pi }{2};\dfrac{{3\pi }}{2}} \right] \Rightarrow - 1 \le \sin \dfrac{{\pi x}}{2} \le 1\\ \Leftrightarrow - 1 \le - \sin \dfrac{{\pi x}}{2} \le 1\end{array}\)
\( \Rightarrow f\left( 1 \right) - 1 \le f\left( x \right) - \sin \dfrac{{\pi x}}{2} \Leftrightarrow g\left( x \right) \ge f\left( 1 \right) - 1 \Rightarrow \mathop {\min }\limits_{\left[ { - 1;3} \right]} g\left( x \right) = f\left( 1 \right) - 1\).
Vậy \(m < f\left( 1 \right) - 1\).
Cho \(f\left( x \right) = \dfrac{1}{{{x^2} - 4x + 5}} - \dfrac{{{x^2}}}{4} + x\). Gọi \(M = \mathop {Max}\limits_{x \in \left[ {0;3} \right]} f\left( x \right);\) \(m = \mathop {Min}\limits_{x \in \left[ {0;3} \right]} f\left( x \right).\) Khi đó\(M-m\) bằng:
Ta có :
\[\begin{array}{l}f\left( x \right) = \dfrac{1}{{{x^2} - 4x + 5}} - \dfrac{{{x^2}}}{4} + x\\f\left( x \right) = \dfrac{1}{{{x^2} - 4x + 5}} - \dfrac{{{x^2} - 4x}}{4}\end{array}\]
Đặt \(t = {x^2} - 4x + 5\) với \(x \in \left[ {0;3} \right]\) ta có \(t' = 2x - 4 = 0 \Leftrightarrow x = 2 \in \left[ {0;3} \right]\).
Ta có : \(t\left( 0 \right) = 5;\,\,t\left( 2 \right) = 1,\,\,t\left( 3 \right) = 2\).
\( \Rightarrow \) Với \(x \in \left[ {0;3} \right]\) thì \(t \in \left[ {1;5} \right]\), khi đó hàm số trở thành \(f\left( t \right) = \dfrac{1}{t} - \dfrac{{t - 5}}{4}\) với \(t \in \left[ {1;5} \right]\).
Ta có \(f'\left( t \right) = - \dfrac{1}{{{t^2}}} - \dfrac{1}{4} < 0\,\,\forall t \in \left[ {1;5} \right]\).
\( \Rightarrow \) Hàm số \(y = f\left( t \right)\) nghịch biến trên \(\left[ {1;5} \right]\) \( \Rightarrow \left\{ \begin{array}{l}\mathop {\max }\limits_{\left[ {0;3} \right]} f\left( x \right) = \mathop {\max }\limits_{\left[ {1;5} \right]} f\left( t \right) = f\left( 1 \right) = 2 = M\\\mathop {\min }\limits_{\left[ {0;3} \right]} f\left( x \right) = \mathop {\min }\limits_{\left[ {1;5} \right]} f\left( t \right) = f\left( 5 \right) = \dfrac{1}{5} = m\end{array} \right.\)
Vậy \(M - m = 2 - \dfrac{1}{5} = \dfrac{9}{5}\).
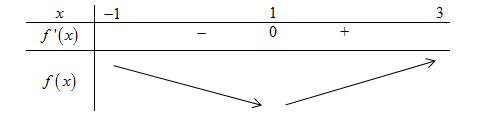
Cho hàm số \(f\left( x \right)\). Biết hàm số \(f'\left( x \right)\) có đồ thị như hình dưới đây. Trên đoạn \(\left[ { - 4;3} \right]\), hàm số \(g\left( x \right) = 2f\left( x \right) + {\left( {1 - x} \right)^2}\) đạt giá trị nhỏ nhất tại điểm
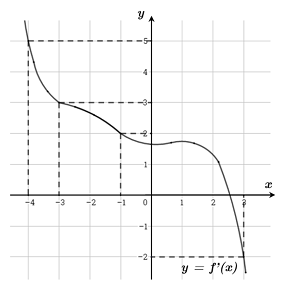
Ta có: \(g'\left( x \right) = 2f'\left( x \right) - 2\left( {1 - x} \right) = 2\left[ {f'\left( x \right) - \left( {1 - x} \right)} \right]\).
Xét \(g'\left( x \right) = 0 \Leftrightarrow f'\left( x \right) = 1 - x\), số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y = f'\left( x \right)\) và đường thẳng \(y = 1 - x\).
Ta biểu diễn đường thẳng \(y = 1 - x\) trên hình vẽ:
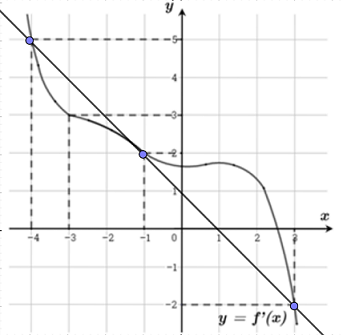
Dựa vào đồ thị hàm số ta thấy \(f'\left( x \right) = 1 - x \Leftrightarrow \left[ \begin{array}{l}x = - 4\\x = - 1\\x = 3\end{array} \right.\)
Từ đó, ta suy ra bảng xét dấu \(g'\left( x \right)\) như sau:
![]()
Vậy hàm số đạt GTNN tại \(x = - 1\).
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình bên:
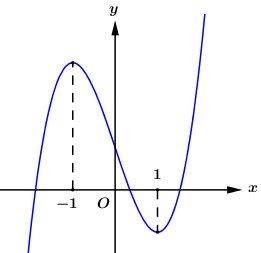
Giá trị nguyên lớn nhất của tham số m để hàm số \(y = f\left( {\left| x \right| - m} \right)\) đồng biến trên khoảng \(\left( {10; + \infty } \right)\) là:
Ta có \(y = f\left( {\left| x \right| - m} \right) = f\left( {\sqrt {{x^2}} - m} \right)\).
\( \Rightarrow y' = \dfrac{{2x}}{{2\sqrt {{x^2}} }}f'\left( {\sqrt {x^2} - m } \right) = \dfrac{x}{{\sqrt {{x^2}} }}f'\left( {\sqrt {x^2} - m } \right)\).
Để hàm số đồng biến trên \(\left( {10; + \infty } \right)\) thì \(y' \ge 0\,\,\forall x \in \left( {10; + \infty } \right)\).
\( \Rightarrow \dfrac{x}{{\sqrt {x^2} }}f'\left( {\sqrt {x^2} - m } \right) \ge 0\,\,\forall x \in \left( {10; + \infty } \right)\) \( \Rightarrow f'\left( {\sqrt {x^2} - m} \right) \ge 0\,\,\forall x \in \left( {10; + \infty } \right)\,\,\left( * \right)\).
Dựa vào đồ thị hàm số ta thấy hàm số đồng biến trên \(\left( {1; + \infty } \right)\) và \(\left( { - \infty ; - 1} \right)\).
Do đó \(\left( * \right) \Leftrightarrow \left[ \begin{array}{l}\sqrt {{x^2}} - m \ge 1\,\,\forall x \in \left( {10; + \infty } \right)\,\,\,\,\,\,\left( 1 \right)\\\sqrt {{x^2}} - m \le - 1\,\,\forall x \in \left( {10; + \infty } \right)\,\,\,\left( 2 \right)\end{array} \right.\)
Xét (1) ta có \(m \le \sqrt {{x^2}} - 1\,\,\forall x \in \left( {10; + \infty } \right) \Rightarrow m \le \mathop {\min }\limits_{\left[ {10; + \infty } \right)} \left( {\sqrt {{x^2}} - 1} \right)\).
Xét \(g\left( x \right) = \sqrt {{x^2}} - 1\) trên khoảng \(\left( {10; + \infty } \right)\) ta có \(g'\left( x \right) = \dfrac{x}{{\sqrt {{x^2}} }} > 0\,\,\forall x \in \left( {10; + \infty } \right)\), do đó hàm số đồng biến trên \(\left( {10; + \infty } \right)\) \( \Rightarrow \mathop {\min }\limits_{\left[ {10; + \infty } \right)} \left( {\sqrt {{x^2}} - 1} \right) = g\left( {10} \right) = 9 \Leftrightarrow m \le 9\).
Xét (2) ta có: \(m \ge \sqrt {{x^2}} + 1\,\,\forall x \in \left( {10; + \infty } \right)\) \( \Rightarrow m \ge \mathop {\max }\limits_{\left[ {10; + \infty } \right)} \left( {\sqrt {{x^2}} + 1} \right)\).
Do \(\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2}} + 1} \right) = + \infty \) nên hàm số đã cho không có GTLN trên \(\left[ {10; + \infty } \right)\), do đó không tồn tại m thỏa mãn (2).
Vậy \(m \le 9\) nên giá trị nguyên lớn nhất của m bằng 9.
Cho hàm số \(y = {x^3} - 3m{x^2} + 3\left( {{m^2} - 1} \right)x + 2020\). Có tất cả bao nhiêu giá trị nguyên của tham số m sao cho hàm số có giá trị nhỏ nhất trên khoảng \(\left( {0; + \infty } \right)\).
Ta có: \(y' = 3{x^2} - 6mx + 3\left( {{m^2} - 1} \right)\).
Cho \(y' = 0 \Leftrightarrow 3{x^2} - 6mx + 3\left( {{m^2} - 1} \right) = 0\) \( \Leftrightarrow {x^2} - 2mx + {m^2} - 1 = 0\).
Ta có \(\Delta ' = {m^2} - {m^2} + 1 = 1 > 0\), khi đó phương trình \(y' = 0\) có 2 nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} = m + 1\\{x_2} = m - 1\end{array} \right.\).
Ta có BBT:
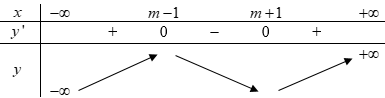
Ta có:
\(\begin{array}{l}f\left( {m - 1} \right) = {m^3} - 3m + 2022\\f\left( {m + 1} \right) = {m^3} - 3m + 2018\end{array}\)
TH1: \(0 < m - 1 \Leftrightarrow m > 1\).
Ta có: \(f\left( 0 \right) = 2020\).
Để hàm số có GTNN trên \(\left( {0; + \infty } \right)\) thì \(f\left( {m + 1} \right) \le f\left( 0 \right) \Leftrightarrow {m^3} - 3m + 2018 \le 2020\) \( \Leftrightarrow {m^3} - 3m - 2 \le 0\).
Xét hàm số \(f\left( m \right) = {m^3} - 3m - 2\) ta có \(f'\left( m \right) = 3{m^2} - 3 = 0 \Leftrightarrow m = \pm 1\),
BBT:
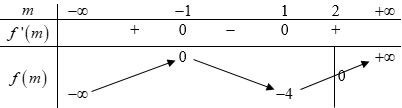
Dựa vào BT ta thấy \(f\left( m \right) \le 0 \Leftrightarrow m \le 2\).
Kết hợp điều kiện \( \Rightarrow 1 < m \le 2\).
TH2: \(m - 1 \le 0 < m + 1 \Leftrightarrow - 1 < m \le 1\), khi đó hàm GTNN của hàm số trên \(\left( {0; + \infty } \right)\) là \(f\left( {m + 1} \right)\).
Kết hợp 2 trường hợp ta có: \(\left[ \begin{array}{l}1 < m \le 2\\ - 1 < m \le 1\end{array} \right.\). Mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ {0;1;2} \right\}\).
Vậy có 3 giá trị của m thỏa mãn yêu cầu bài toán.
Cho \(x,\,\,y\) là các số thực thỏa mãn \({2^{x + y - 1}}\left( {{3^{x + y}} + 1} \right) = 3x + 3y + 1\). Tìm giá trị nhỏ nhất của biểu thức \(P = {x^2} + xy + {y^2}\).
Ta có:
\(\begin{array}{l}{2^{x + y - 1}}\left( {{3^{x + y}} + 1} \right) = 3x + 3y + 1\\ \Leftrightarrow {2^{x + y}}\left( {{3^{x + y}} + 1} \right) = 6x + 6x + 2\\ \Leftrightarrow {6^{x + y}} + {2^{x + y}} = 6\left( {x + y} \right) + 2\end{array}\)
Đặt \(x + y = t\), phương trình trở thành \({6^t} + {2^t} = 6t + 2\) \( \Leftrightarrow {6^t} + {2^t} - 6t - 2 = 0\)
Xét hàm số \(f\left( t \right) = {6^t} + {2^t} - 6t - 2\) ta có:
\(\begin{array}{l}f'\left( t \right) = {6^t}.\ln 6 + {2^t}.\ln 2 - 6\\f''\left( t \right) = {6^t}{\ln ^2}6 + {2^t}.{\ln ^2}2 > 0\,\,\,\forall t \in \mathbb{R}\end{array}\)
Do đó hàm số \(y = f'\left( t \right)\) đồng biến trên \(\mathbb{R}\), suy ra phương trình \(f'\left( t \right) = 0\) có nhiều nhất 1 nghiệm.
Suy ra phương trình \(f\left( t \right) = 0\) có nhiều nhất 2 nghiệm.
Ta lại có: \(\left\{ \begin{array}{l}f\left( 0 \right) = {6^0} + {2^0} - 6.0 - 2 = 0\\f\left( 1 \right) = {6^1} + {2^1} - 6.1 - 2 = 0\end{array} \right.\), do đó phương trình \(f\left( t \right) = 0\) có đúng hai nghiệm \(t = 0\), \(t = 1\).
\( \Rightarrow \left[ \begin{array}{l}x + y = 0\\x + y = 2\end{array} \right.\)
TH1: \(x + y = 0 \Rightarrow y = - x\).
Thay vào \(P\) ta có: \(P = {x^2} + xy + {y^2} = {x^2} \ge 0\).
TH2: \(x + y = 1 \Leftrightarrow y = 1 - x\).
Thay vào \(P\) ta có:
\(\begin{array}{l}P = {x^2} + x\left( {1 - x} \right) + {\left( {1 - x} \right)^2}\\=x^2-x+1\\= {\left( {x - \dfrac{1}{2}} \right)^2} + \dfrac{3}{4} \ge \dfrac{3}{4} \end{array}\).
Vậy giá trị nhỏ nhất của \(P\) là \(0\), đạt được khi \(x + y = 0\).
Cho các số thực \(x,\,\,y\) thay đổi thỏa mãn \({x^2} + 2{y^2} + 2xy = 1\) và hàm số \(f\left( t \right) = {t^4} - {t^2} + 2\). Gọi \(M,\,\,m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của \(Q = f\left( {\dfrac{{x + y + 1}}{{x + 2y - 2}}} \right)\). Tính \(M + m\)?
Ta có: \({x^2} + 2{y^2} + 2xy = 1 \Leftrightarrow {\left( {x + y} \right)^2} + {y^2} = 1\)
Đặt \(\left\{ \begin{array}{l}x + y = \sin \alpha \\y = {\rm{cos}}\alpha \end{array} \right.\). Ta có: \(Q = f\left( {\dfrac{{x + y + 1}}{{x + 2y - 2}}} \right) = f\left( {\dfrac{{\sin \alpha + 1}}{{\sin \alpha + {\rm{cos}}\,\alpha - 2}}} \right)\)
Đặt \(t = \dfrac{{\sin \alpha + 1}}{{\sin \alpha + {\rm{cos}}\,\alpha - 2}}\). Ta có: \(Q = f\left( {\dfrac{{\sin \alpha + 1}}{{\sin \alpha + {\rm{cos}}\,\alpha - 2}}} \right) = f\left( t \right)\)
\(t = \dfrac{{\sin \alpha + 1}}{{\sin \alpha + {\rm{cos}}\,\alpha - 2}}\,\,\left( {\alpha \in \mathbb{R}} \right) \Leftrightarrow t\sin \alpha + t{\rm{cos}}\,\alpha - 2t = \sin \alpha + 1 \Leftrightarrow \left( {t - 1} \right)\sin \alpha + t\,{\rm{cos}}\,\alpha = 2t + 1\) (*)
Để phương trình (*) tồn tại nghiệm \(\alpha \) thì \({\left( {t - 1} \right)^2} + {t^2} \ge {\left( {2t + 1} \right)^2}\)
\( \Leftrightarrow {t^2} - 2t + 1 + {t^2} \ge 4{t^2} + 4t + 1\)\( \Leftrightarrow 2{t^2} + 6t \le 0 \Leftrightarrow - 3 \le t \le 0\)
Xét \(Q = f\left( t \right) = {t^4} - {t^2} + 2\) trên đoạn \(\left[ { - 3;0} \right]\), có: \(f'\left( t \right) = 4{t^3} - 2t,\,\,f'\left( t \right) = 0 \Leftrightarrow \left[ \begin{array}{l}t = 0\\t = \pm \sqrt {\dfrac{1}{2}} \end{array} \right.\)
Hàm số \(f\left( t \right)\) liên tục trên \(\left[ { - 3;0} \right]\), có \(f\left( { - 3} \right) = 74,\,f\left( { - \sqrt {\dfrac{1}{2}} } \right) = \dfrac{7}{4},\,f\left( 0 \right) = 2\)\( \Rightarrow \mathop {\min }\limits_{\left[ { - 3;0} \right]} f\left( t \right) = \dfrac{7}{4},\,\mathop {\max }\limits_{\left[ { - 3;0} \right]} f\left( t \right) = 74\)
\( \Rightarrow \)M + m\( = \dfrac{7}{4} + 74 = \dfrac{{303}}{4}\).
Cho hàm số \(y = \dfrac{{x + 1}}{{x - 1}}\) có đồ thị là \(\left( C \right)\). Gọi \(M\left( {{x_M};{y_M}} \right)\) là một điểm bất kỳ trên \(\left( C \right)\). Khi tổng khoảng cách từ \(M\)đến hai trục tọa độ là nhỏ nhất, tính tổng \({x_M} + {y_M}\).
Đặt \(M\left( {x;\dfrac{{x + 1}}{{x - 1}}} \right) \in \left( C \right).\)
Khi đó ta có: \(\left\{ \begin{array}{l}d\left( {M;Ox} \right) = \left| {{y_M}} \right| = \left| {\dfrac{{x + 1}}{{x - 1}}} \right|\\d\left( {M;Oy} \right) = \left| {{x_M}} \right| = \left| x \right|\end{array} \right.\)
Tổng khoảng cách từ M đến hai trục tọa độ là \(S = \left| x \right| + \left| {\dfrac{{x + 1}}{{x - 1}}} \right| \ge \left| {x + \dfrac{{x + 1}}{{x - 1}}} \right|.\)
Dấu bằng xảy ra khi \(x.\dfrac{{x + 1}}{{x - 1}} \ge 0 \Leftrightarrow \left[ \begin{array}{l}x > 1\\ - 1 \le x \le 0\end{array} \right.\)
Đặt \(f\left( x \right) = x + \dfrac{{x + 1}}{{x - 1}} = \dfrac{{{x^2} + 1}}{{x - 1}}\)
\( \Rightarrow f'\left( x \right) = \dfrac{{{x^2} - 2x - 1}}{{{{\left( {x - 1} \right)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1 - \sqrt 2 \\x = 1 + \sqrt 2 \end{array} \right.\)
Bảng biến thiên:
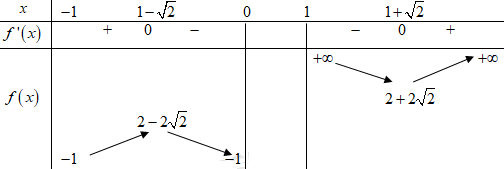
Dựa vào bảng biến thiên ta thấy \(\left| {x + \dfrac{{x + 1}}{{x - 1}}} \right| \ge \left| {2 - 2\sqrt 2 } \right| = 2\sqrt 2 - 2.\)
Dấu bằng xảy ra khi \(x = 1 - \sqrt 2 \Rightarrow y = 1 - \sqrt 2 \Rightarrow {x_M} + {y_M} = 2 - 2\sqrt 2 .\)
Đề thi THPT QG - 2021 - mã 101
Trên đoạn \(\left[ {0;3} \right]\), hàm số \(y = - {x^3} + 3x\) đạt giá trị lớn nhất tại điểm
Khảo sát hàm số \(y = - {x^3} + 3x\) trên \(\left[ {0;3} \right]\).
+ \(y' = - 3{x^2} + 3 = 0 \Leftrightarrow x = \pm 1\).
+ BBT:
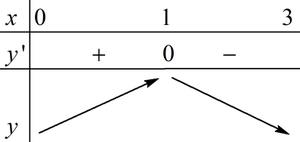
\( \Rightarrow \) Hàm số đạt giá trị lớn nhất tại \(x = 1\).
Cho một tấm tôn hình vuông có cạnh bằng a. Người ta cắt 4 góc của tấm tôn để được một tấm tôn mới như hình vẽ.
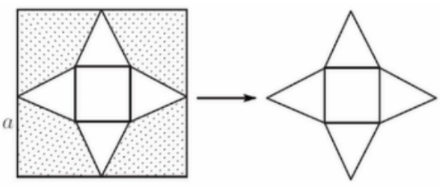
Từ tấm tôn mới, người ta gặp được một hình chóp tứ giác đều. Để khối chóp thu được có thể tích lớn nhất thì diện tích các miếng tôn bỏ đi là
Gọi x là độ dài của cạnh đáy của khối chóp
\(h\) là chiều cao của khối chóp, \(h'\) là chiều cao của tam giác cân ở mặt bên của khối chóp.
Bước 1: Biểu diễn h và thể tích V của khối chóp theo a và x
Ta có: \(x + 2h' = a\)\( \Rightarrow h' = \dfrac{{a - x}}{2}\)
Ta có: \({h^2} + {\left( {\dfrac{x}{2}} \right)^2} = {\left( {\dfrac{{a - x}}{2}} \right)^2}\) \( \Leftrightarrow h = \sqrt {{{\left( {\dfrac{{a - x}}{2}} \right)}^2} - {{\left( {\dfrac{x}{2}} \right)}^2}} = \dfrac{{\sqrt {{a^2} - 2ax} }}{2}\)
Thể tích khối chóp: \(V = \dfrac{1}{3}.\dfrac{{\sqrt {{a^2} - 2ax} }}{2}.{x^2}\)
\( = \dfrac{1}{6}\sqrt { - 2a{x^5} + {a^2}{x^4}} \)
Bước 2: Tìm max của \(f\left( x \right) = - 2a{x^5} + {a^2}{x^4}\) với x>0
Xét hàm số \(f\left( x \right) = - 2a{x^5} + {a^2}{x^4}\) với x>0
\({V_{\max }} \Leftrightarrow f{\left( x \right)_{\max }}\)
Ta có: \(f'\left( x \right) = - 10a{x^4} + 4{a^2}{x^3}\)
\(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \dfrac{{2a}}{5}\end{array} \right.\)
\( \Rightarrow \max f\left( x \right) = f\left( {\dfrac{{2a}}{5}} \right) = \dfrac{{16{a^6}}}{{3125}}\)
Dấu “=” xảy ra khi và chỉ khi \(x = \dfrac{{2a}}{5}\)
Bước 3: Tìm phần diện tích bị bỏ
\( \Rightarrow\) Diện tích phần không bị bỏ là:
\(S = {x^2} + 4.\dfrac{1}{2}.x.\dfrac{{a - x}}{2} = \dfrac{{2{a^2}}}{5}\)
Diện tích bị bỏ là \(\dfrac{{3{a^2}}}{5}\)

