Cho hàm số \(y = \dfrac{{x + 1}}{{x - 1}}\) có đồ thị là \(\left( C \right)\). Gọi \(M\left( {{x_M};{y_M}} \right)\) là một điểm bất kỳ trên \(\left( C \right)\). Khi tổng khoảng cách từ \(M\)đến hai trục tọa độ là nhỏ nhất, tính tổng \({x_M} + {y_M}\).

Đặt \(M\left( {x;\dfrac{{x + 1}}{{x - 1}}} \right) \in \left( C \right).\)

Khi đó ta có: \(\left\{ \begin{array}{l}d\left( {M;Ox} \right) = \left| {{y_M}} \right| = \left| {\dfrac{{x + 1}}{{x - 1}}} \right|\\d\left( {M;Oy} \right) = \left| {{x_M}} \right| = \left| x \right|\end{array} \right.\)

Tổng khoảng cách từ M đến hai trục tọa độ là \(S = \left| x \right| + \left| {\dfrac{{x + 1}}{{x - 1}}} \right| \ge \left| {x + \dfrac{{x + 1}}{{x - 1}}} \right|.\)

Dấu bằng xảy ra khi \(x.\dfrac{{x + 1}}{{x - 1}} \ge 0 \Leftrightarrow \left[ \begin{array}{l}x > 1\\ - 1 \le x \le 0\end{array} \right.\)

Đặt \(f\left( x \right) = x + \dfrac{{x + 1}}{{x - 1}} = \dfrac{{{x^2} + 1}}{{x - 1}}\)

\( \Rightarrow f'\left( x \right) = \dfrac{{{x^2} - 2x - 1}}{{{{\left( {x - 1} \right)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1 - \sqrt 2 \\x = 1 + \sqrt 2 \end{array} \right.\)

Bảng biến thiên:

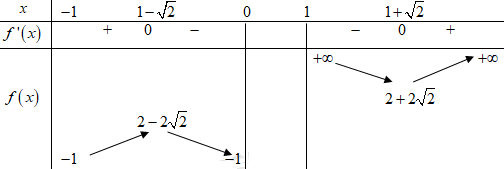
Dựa vào bảng biến thiên ta thấy \(\left| {x + \dfrac{{x + 1}}{{x - 1}}} \right| \ge \left| {2 - 2\sqrt 2 } \right| = 2\sqrt 2  - 2.\)

Dấu bằng xảy ra khi \(x = 1 - \sqrt 2  \Rightarrow y = 1 - \sqrt 2  \Rightarrow {x_M} + {y_M} = 2 - 2\sqrt 2 .\)