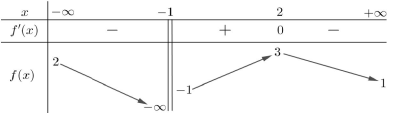
Cho hàm số \(y = {x^3} - 3m{x^2} + 3\left( {{m^2} - 1} \right)x + 2020\). Có tất cả bao nhiêu giá trị nguyên của tham số m sao cho hàm số có giá trị nhỏ nhất trên khoảng \(\left( {0; + \infty } \right)\).

Ta có: \(y' = 3{x^2} - 6mx + 3\left( {{m^2} - 1} \right)\).

Cho \(y' = 0 \Leftrightarrow 3{x^2} - 6mx + 3\left( {{m^2} - 1} \right) = 0\) \( \Leftrightarrow {x^2} - 2mx + {m^2} - 1 = 0\).

Ta có \(\Delta ' = {m^2} - {m^2} + 1 = 1 > 0\), khi đó phương trình \(y' = 0\) có 2 nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} = m + 1\\{x_2} = m - 1\end{array} \right.\).

Ta có BBT:

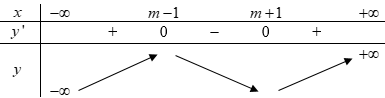
Ta có:

\(\begin{array}{l}f\left( {m - 1} \right) = {m^3} - 3m + 2022\\f\left( {m + 1} \right) = {m^3} - 3m + 2018\end{array}\)

TH1: \(0 < m - 1 \Leftrightarrow m > 1\).

Ta có: \(f\left( 0 \right) = 2020\).

Để hàm số có GTNN trên \(\left( {0; + \infty } \right)\) thì \(f\left( {m + 1} \right) \le f\left( 0 \right) \Leftrightarrow {m^3} - 3m + 2018 \le 2020\) \( \Leftrightarrow {m^3} - 3m - 2 \le 0\).

Xét hàm số \(f\left( m \right) = {m^3} - 3m - 2\) ta có \(f'\left( m \right) = 3{m^2} - 3 = 0 \Leftrightarrow m =  \pm 1\),

BBT:

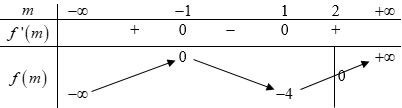
Dựa vào BT ta thấy \(f\left( m \right) \le 0 \Leftrightarrow m \le 2\).

Kết hợp điều kiện \( \Rightarrow 1 < m \le 2\).

TH2: \(m - 1 \le 0 < m + 1 \Leftrightarrow  - 1 < m \le 1\), khi đó hàm GTNN của hàm số trên \(\left( {0; + \infty } \right)\) là \(f\left( {m + 1} \right)\).

Kết hợp 2 trường hợp ta có: \(\left[ \begin{array}{l}1 < m \le 2\\ - 1 < m \le 1\end{array} \right.\). Mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ {0;1;2} \right\}\).

Vậy có 3 giá trị của m thỏa mãn yêu cầu bài toán.