Trả lời bởi giáo viên
Đáp án đúng: b
Xét hàm số y=f(x)=x3−3x2+m trên [1;3], có f′(x)=3x2−6x,f′(x)=0⇔[x=0(L)x=2
Bảng biến thiên:
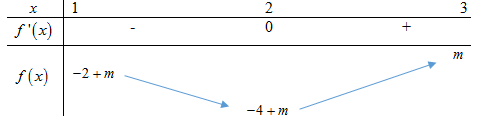
min[1;3]|x3−3x2+m|≥2⇒[m−4>0m<0
TH1: m−4>0⇔m>4
min[1;3]|x3−3x2+m|≥2⇔m−4≥2⇔m≥6
Mà m∈[−5;5]⇒m∈∅
TH2: m<0
min[1;3]|x3−3x2+m|≥2⇔−m≥2⇔m≤−2
Mà m∈[−5;5],m∈Z⇒m∈{−5;−4;−3;−2}: 4 giá trị.
Hướng dẫn giải:
Xét hàm số y=f(x)=x3−3x2+m trên [1;3], lập BBT từ đó xét các trường hợp.
Tìm GTLN – GTNN của hàm số y=|f(x)| trên đoạn [a;b]
Bước 1: Tìm GTLN – GTNN của hàm số y=f(x) trên đoạn [a;b], giả sử lần lượt là M và m.
Bước 2:
+) Tìm maxy[a;b]=max{|M|;|m|}
+) Tìm miny[a;b]
- Trường hợp 1: M.m<0⇒miny[a;b]=0
- Trường hợp 2: m≥0⇒miny[a;b]=m
- Trường hợp 3: M≤0⇒miny[a;b]=|M|=−M