I. Định nghĩa
Cho hai điểm cố định \({F_1},\,\,{F_2}\) với \({F_1}{F_2} = 2c\left( {c > 0} \right)\) và hằng số \(a > c\).
Elip $(E)$ là tập hợp các điểm $M$ thỏa mãn \(M{F_1} + M{F_2} = 2a\).
Các điểm \({F_1},\,\,{F_2}\) là tiêu điểm của $(E).$
Khoảng cách \({F_1}{F_2} = 2c\) là tiêu cự của $(E).$
\(M{F_1},\,\,M{F_2}\) được gọi là bán kính qua tiêu.
II. Phương trình chính tắc của elip
Với \({F_1}\left( { - c;0} \right),\,\,{F_2}\left( {c;0} \right)\):
$M\left( {x;y} \right) \in \left( E \right) \Leftrightarrow \dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\,\,\,\left( 1 \right)$ trong đó \({b^2} = {a^2} - {c^2}\)
(1) được gọi là phương trình chính tắc của $(E)$
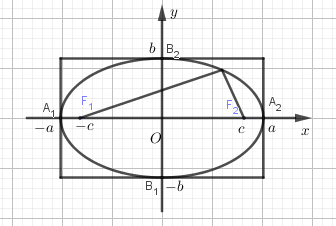
III. Hình dạng và tính chất của elip
Elip có phương trình $(1)$ nhận các trục tọa độ là trục đối xứng và gốc tọa độ làm tâm đối xứng.
+ Tiêu điểm: Tiêu điểm trái \({F_1}\left( { - c;0} \right)\), tiêu điểm phải \({F_2}\left( {c;0} \right)\)
+ Các đỉnh: \({A_1}\left( { - a;0} \right),\,\,{A_2}\left( {a;0} \right),\) \({B_1}\left( {0; - b} \right),\,\,{B_2}\left( {0;b} \right)\)
+ Trục lớn: \({A_1}{A_2} = 2a\), nằm trên trục $Ox;$ trục nhỏ :\({B_1}{B_2} = 2b\), nằm trên trục $Oy$
+ Hình chữ nhật tạo bởi các đường thẳng \(x = \pm a,\,y = \pm b\) gọi là hình chữ nhật cơ sở.
+ Tâm sai: \(e = \dfrac{c}{a} < 1\)
+ Bán kính qua tiêu điểm của điểm \(M\left( {{x_M};{y_M}} \right)\) thuộc $(E)$ là:
\(M{F_1} = a + e{x_M} = a + \dfrac{c}{a}{x_M},\) \(M{F_2} = a - e{x_M} = a - \dfrac{c}{a}{x_M}\)
