Đề thi tư duy định lượng - Đề số 5

Dựa vào các thông tin dưới đây để trả lời câu hỏi:

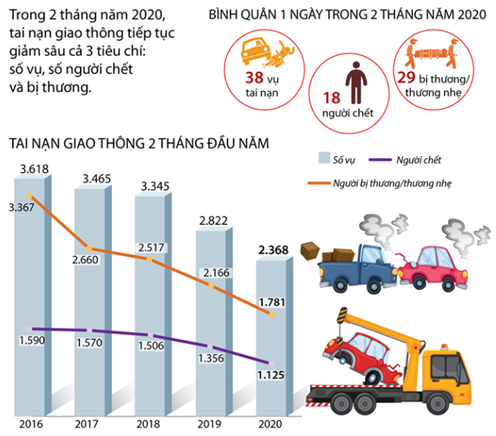
Số vụ tai nạn năm 2020 trong hai tháng đầu năm giảm bao nhiêu vụ?

Số giá trị nguyên của tham số \(m\) để phương trình \(\sqrt {{x^2} - mx + 3}  = \sqrt {2x - 1} \) có hai nghiệm phân biệt là

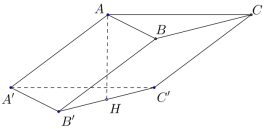
Cho hình lăng trụ \(ABC.A'B'C'\) có tam giác \(ABC\) vuông tại \(A\), \(AB = a\), \(AC = a\sqrt 3 \), \(AA' = 2a\). Hình chiếu vuông góc của điểm \(A\) trên mặt phẳng \(\left( {A'B'C'} \right)\) trùng với trung điểm \(H\) của đoạn \(B'C'\) (tham khảo hình vẽ dưới đây). Khoảng cách giữa hai đường thẳng \(AA'\) và \(BC'\) bằng \(\dfrac{{a\sqrt {m} }}{5}\). Tìm $m$.

Một số tự nhiên có hai chữ số có dạng \(\overline {ab} \), biết hiệu của hai chữ số đó bằng \(3\). Nếu viết các chữ số theo thứ tự ngược lại thì được một số bằng \(\dfrac{4}{5}\) số ban đầu trừ đi \(10\). Khi đó \({a^2} + {b^2}\) bằng

Cho biểu thức \(f\left( x \right) = \dfrac{{2 - x}}{{x + 1}} + 2.\) Tập hợp tất cả các giá trị của \(x\) thỏa mãn bất phương trình \(f\left( x \right) < 0\) là

Trong mặt phẳng với hệ toạ độ $Oxy$, cho $2$ đường thẳng ${d_1}:x - 7y + 17 = 0,$

 ${d_2}:x + y - 5 = 0.$ Viết phương trình đường thẳng $d$ qua điểm $M\left( {0;1} \right)$ tạo với ${d_1},{d_2}$ một tam giác cân tại giao điểm của ${d_1},{d_2}$.

Trong mặt phẳng với hệ trục tọa độ Oxy, cho phương trình đường tròn \(\left( {{C_m}} \right):{x^2} + {y^2} - 2mx + \left( {4m + 2} \right)y - 6m - 5 = 0\) (m là tham số). Tập hợp các điểm \({I_m}\) là tâm của đường tròn \(\left( {{C_m}} \right)\) khi m thay đổi là:

Tập nghiệm của phương trình \(\tan x.\cot x = 1\) là:

Một gia đình cần khoan một cái giếng để lấy nước. Họ thuê một đội khoan giếng nước đến để khoan giếng nước. Biết giá của mét khoan đầu tiên là 80.000 đồng, kể từ mét khoan thứ 2 giá của mỗi mét khoan tăng thêm 5000 đồng so với giá của mét khoan trước đó. Biết cần phải khoan sâu xuống 50m mới có nước. Vậy hỏi phải trả bao nhiêu tiền để khoan cái giếng đó?

Điền số thích hợp vào ô trống:

Có 5 cuốn sách toán khác nhau và 5 cuốn sách văn khác nhau. Có bao nhiêu cách sắp xếp chúng thành 1 hàng sao cho các cuốn sách cùng môn thì đứng kề nhau?

Có hai hộp chứa bi. Hộp thứ nhất chứa $4$ viên bi đỏ và $3$ viên bi trắng, hộp thứ hai chứa $2 $ viên bi đỏ và $4$ viên bi trắng. Lấy ngẫu nhiên từ mỗi hộp ra một viên bi, tính xác suất để $2$ viên lấy ra cùng màu.

Cho giới hạn \(I = \mathop {\lim }\limits_{x \to 0} \dfrac{{{e^{3x}} - {e^{2x}}}}{x}\), chọn mệnh đề đúng:

Tính đạo hàm của hàm số \(f\left( x \right) = x\left( {x - 1} \right)\left( {x - 2} \right)...\left( {x - 2018} \right)\) tại điểm \(x = 0\).

Cho hình chóp $S.ABCD$ có đáy $ABCD$  là hình thang có đáy lớn $BC$ , đáy nhỏ $AD$.  Mặt bên $\left( {SAD} \right)$  là tam giác đều, \(\left( \alpha  \right)\) là mặt phẳng đi qua $M$  trên cạnh $AB$ , song song với $SA,BC$ . Mp\(\left( \alpha  \right)\)cắt các cạnh $CD,SC,SB$  lần lượt tại $N,P,Q.MNPQ$  là hình gì?

Cho hình chóp \(S.ABC\) có \(SA\) vuông góc với mặt phẳng \(\left( {ABC} \right)\), \(SA = \dfrac{{a\sqrt 3 }}{2}\), tam giác \(ABC\) đều cạnh bằng \(a\) (minh họa như hình dưới). Góc  tạo bởi giữa mặt phẳng\((SBC)\) và \(\left( {ABC} \right)\) bằng

 Tìm họ nguyên hàm \(\int{{{\sin }^{2}}x\,\text{d}x}.\)

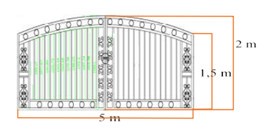
Ba Tí muốn làm cửa sắt được thiết kế như hình bên. Vòm cổng có hình dạng một parabol. Giá \(1{m^2}\) cửa sắt là \(660\,000\) đồng. Cửa sắt có giá (nghìn đồng) là:  

Cho \(2\sqrt 3 m - \int\limits_0^1 {\dfrac{{4{x^3}}}{{{{\left( {{x^4} + 2} \right)}^2}}}dx}  = 0\). Khi đó \(144{m^2} - 1\) bằng:

Cho hàm số \(y = f\left( x \right)\)  thỏa mãn \(\int\limits_0^1 {\left( {x + 1} \right)f'\left( x \right)dx}  = 10\)  và \(2f\left( 1 \right) - f\left( 0 \right) = 2\). Tính \(I = \int\limits_0^1 {f\left( x \right)dx} \)

Tính thể tích của vật thể nằm giữa hai mặt phẳng $x =1$ và $x = 2$ , biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ $x , (1 ≤ x ≤ 2)$ là một hình chữ nhật có độ dài hai cạnh là \(x\) và \(\sqrt {{x^2} + 3} \).

Biết thể tích khí CO2 năm 1998 và \(V\,\,\left( {{m^3}} \right)\). 10 năm tiếp theo, mỗi năm thể tích \(C{O_2}\) tăng m%, 10 năm tiếp nữa, thể tích CO2 mỗi năm tăng n%. Tính thể tích CO2 năm 2018?

Tìm số nghiệm nguyên của bất phương trình \({\left( {\dfrac{1}{3}} \right)^{\sqrt {{x^2} - 3x - 10} }} > {\left( {\dfrac{1}{3}} \right)^{x - 2}}\)

Tìm $m$ để phương trình \({4^x} - {\text{ }}{2^{x{\text{ }} + {\text{ }}3}} + {\text{ }}3{\text{ }} = {\text{ }}m\) có đúng 2 nghiệm $x \in \left( {1;3} \right)$ .

Có bao nhiêu số nguyên \(m\) để hàm số \(y = \dfrac{1}{3}{x^3} - m{x^2} + \left( {m + 2} \right)x + 2018\) không có cực trị?

Ký hiệu \(M\) và \(m\) tương ứng là GTLN và GTNN của hàm số \(y = {x^2} - 2x + 5\) trên miền \(\left[ {2;7} \right].\) Biết rằng M=km. Tìm k?

Khối chóp tam giác có độ dài 3 cạnh xuất phát từ một đỉnh là \(a,\,\,2a,\,\,3a\) có thể tích lớn nhất bằng

Cho $2$ số phức,\({z_1} = 1 + 3i,{\overline z _2} = 4 + 2i\). Tính môđun của số phức ${z_2} - 2{z_1}$

Tìm tập hợp các điểm trên mặt phẳng tọa độ biểu diễn các số phức $z$ thỏa mãn điều kiện \(2|z - 1 - 2i| = |3i + 1 - 2\bar z|\).

Gọi $(H)$ là tập hợp các điểm biểu diễn số phức $z$ thỏa mãn $1 \leq|z-1| \leq 2$ trong mặt phẳng phức. Khi đó, diện tích hình $(H)$ bằng

Cho hai số phức \({z_1} = 2 + 3i\) và \({z_2} = 3 - 2i.\) Tọa độ điểm biểu diễn số phức \({z_1} - {z_2}\) là:

Trong không gian với hệ tọa độ Oxyz cho. \(A(1; -1; 2); B(2; 1; 1)\) và mặt phẳng (P):\( x + y + z + 1 = 0\). Mặt phẳng \((Q)\) chứa \(A, B\) và vuông góc với mặt phẳng \((P)\). Mặt phẳng \((Q)\) có phương trình là:

Trong không gian \(Oxyz,\) cho hai mặt phẳng \(\left( P \right):x + 2y - 2z - 6 = 0\) và \(\left( Q \right):x + 2y - 2z + 3 = 0\). Khoảng cách giữa hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) bằng

Trong không gian \(Oxyz\), tọa độ điểm đối xứng với điểm \(Q\left( {2;7;5} \right)\) qua mặt phẳng \(\left( {Oxz} \right)\) là

Trong không gian với hệ tọa độ $Oxyz$ , cho đường thẳng \(d:\left\{ \begin{array}{l}x = t\\y =  - 1\\z =  - t\end{array} \right.\) và 2 mặt phẳng $(P)$  và $(Q)$ lần lượt có phương  trình $x + 2y + 2z + 3 = 0;x + 2y + 2z + 7 = 0$. Viết phương trình mặt cầu $(S)$ có tâm$I$  thuộc đường thẳng $d$, tiếp xúc với hai mặt phẳng $(P)$  và $(Q)$.

Trong không gian Oxyz, gọi d là đường thẳng đi qua điểm \(M\left( {2;1;1} \right)\), cắt và vuông góc với đường thẳng \(\Delta :\dfrac{{x - 2}}{{ - 2}} = \dfrac{{y - 8}}{1} = \dfrac{z}{1}\). Tìm tọa độ giao điểm của d và mặt phẳng \(\left( {Oyz} \right)\).

Trong không gian với hệ tọa độ \(Oxyz\), cho tam giác \(ABC\) có \(A\left( {1;2; - 1} \right)\), \(B\left( {2; - 1;3} \right)\), \(C\left( { - 4;7;5} \right)\). Tọa độ chân đường phân giác trong góc \(\widehat B\) của tam giác \(ABC\) là:

Trong không gian \(Oxyz\), khoảng cách từ gốc tọa độ \(O\) đến mặt phẳng \(\left( P \right):x - y + 2z - 3 = 0\) bằng  \( \dfrac{{\sqrt 6 }}{a}\). Tìm $a$.

Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng ${\Delta _1}:\dfrac{{x - 2}}{1} = \dfrac{{y + 1}}{2} = \dfrac{{z - 1}}{{ - {\mkern 1mu} 3}}$ và ${\Delta _2}:\left\{ \begin{array}{l}x = t\\{\rm{ \;}}y = 2 - t\\{\rm{ \;}}z = 1 + 2t\end{array} \right.$. Phương trình mặt phẳng $\left( {\alpha {\rm{\;}}} \right)$ song song với hai đường thẳng ${\Delta _1},{\mkern 1mu} {\mkern 1mu} {\Delta _2}$ và cách điểm \(I\left( {1; - 1;3} \right)\) một khoảng bằng $\dfrac{{\sqrt {35} }}{5}$ là

Trong không gian cho hai điểm \(M\left( {0;1;3} \right)\) và \(N\left( {1;0;1} \right)\). Sin của góc hợp bởi hai véc tơ \(\overrightarrow {OM} ,\overrightarrow {ON} \) là:

Một sợi dây (không co giãn) được quấn đối xứng đúng 10 vòng quanh một ống trụ tròn đều có bán kính \(R = \dfrac{2}{\pi }\,\,cm\) (như hình vẽ).

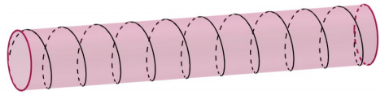
Biết rằng sợi dây có chiều dài 50 cm. Hãy tính diện tích xung quanh của ống trụ đó.

Cho hình chóp \(S.ABC\) có \(SA \bot SB,SB \bot SC,SA \bot SC;SA = 2a,SB = b,SC = c\). Thể tích khối chóp là:

Trong tất cả các giá trị của tham số $m$ để hàm số $y = \dfrac{1}{3}{x^3} + m{x^2} - mx - m$ đồng biến trên $R$, giá trị nhỏ nhất của $m$ là:

Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và có bảng xét dấu đạo hàm như sau:

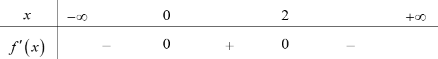
Tổng giá trị tất cả các điểm cực trị của hàm số \(y = f\left( {x - 2019} \right) + 2020\) là:

Hàm số \(f\left( x \right) = {x^4}{\left( {x - 1} \right)^2}\) có bao nhiêu điểm cực trị?

Tìm $m$ để $({C_m})$ : $y = {x^4} - 2m{x^2} + 2$ có $3$ điểm cực trị là $3$ đỉnh của một tam giác vuông cân.

Cho hình chóp đều \(S.ABCD\) có cạnh \(AB = a\), góc giữa đường thẳng \(SA\) và mặt phẳng \(\left( {ABC} \right)\) bằng \(45^0\). Thể tích khối chóp \(S.\,ABCD\) là

Viết phương trình tiếp tuyến của đồ thị hàm số $y =  - 2{x^3} + 4x + 2$ tại điểm có hoành độ bằng $0.$

Một người tham gia chương trình bảo hiểm An sinh xã hội của công ty Bảo Việt với thể lệ như sau: Cứ đến tháng $9$ hàng năm người đó đóng vào công ty là $12$ triệu đồng với lãi suất hàng năm không đổi là $6\% $ / năm. Hỏi sau đúng $18$ năm kể từ ngày đóng, người đó thu về được tất cả bao nhiêu tiền? Kết quả làm tròn đến hai chữ số phần thập phân.

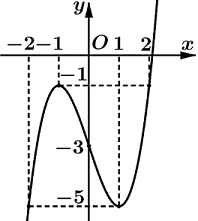
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) có đồ thị như hình vẽ dưới đây.

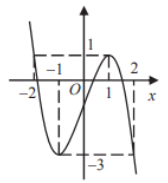
Hỏi phương trình \(f\left( {2 - f\left( x \right)} \right) = 1\) có tất cả bao nhiêu nghiệm thực phân biệt?

Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên \(\mathbb{R}\), có đồ thị như hình vẽ bên. Tìm giá trị nhỏ nhất \(m\) và giá trị lớn nhất \(M\) của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ { - 2;2} \right]\).