Đề thi tư duy định lượng - Đề số 6
Kỳ thi ĐGNL ĐHQG Hà Nội
Kết quả:
0/50
Thời gian làm bài: 00:00:00
Hà Nội tính đến 10 giờ 45 (giờ VN) ngày 16/12/2020 đã có 15 quốc gia ghi nhận số ca mắc COVID-19 trên 1 triệu.
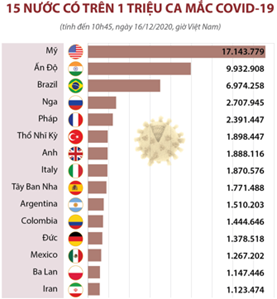
(Nguồn: Worldometers.info)
Tính đến thời điểm đó, Quốc gia nào có số ca mắc Covid 19 – nhiều nhất thế giới?
Gọi \(S\) là tập nghiệm của phương trình \(\sqrt {5{x^2} + 4x} - \sqrt {{x^2} - 3x - 18} = 5\sqrt x \). Số phần tử của \(S\) là:
Cho hình chóp $S.ABCD$ có đáy $ABCD $ là hình vuông cạnh bằng \(10\). Cạnh bện $SA$ vuông góc với mặt phẳng $(ABCD)$ và $SC = 10\sqrt 5 $. Gọi $M, N$ lần lượt là trung điểm của $SA$ và $CD.$ Tính khoảng cách giữa BD và MN.
Hệ phương trình \(\left\{ \begin{array}{l}{\left( {2x + y} \right)^2} - 5\left( {4{x^2} - {y^2}} \right) + 6\left( {4{x^2} - 4xy + {y^2}} \right) = 0\\2x + y + \dfrac{1}{{2x - y}} = 3\end{array} \right.\) có một nghiệm \(\left( {{x_0}; {y_0}} \right)\) thỏa mãn \({x_0} > \dfrac{1}{2}\). Khi đó \(P = {x_0} + y_0^2\) có giá trị là
Lập phương trình đường phân giác trong của góc $A$ của \(\Delta ABC\) biết \(A\left( {2;0} \right);B\left( {4;1} \right);C\left( {1;2} \right)\)
Giải phương trình \(\sin 18x\cos 13x = \sin 9x\cos 4x\).
Có hai cơ sở khoan giếng A và B. Cơ sở A giá mét khoan đầu tiên là \(8000\) (đồng) và kể từ mét khoan thứ hai, giá của mỗi mét sau tăng thêm \(500\) (đồng) so với giá của mét khoan ngay trước đó. Cơ sở B: Giá của mét khoan đầu tiên là \(6000\) (đồng) và kể từ mét khoan thứ hai, giá của mỗi mét khoan sau tăng thêm \(7\% \) giá của mét khoan ngay trước đó. Một công ty giống cây trồng muốn thuê khoan hai giếng với độ sâu lần lượt là \(20\)$\left( {\rm{m}} \right)$ và \(25\)$\left( {\rm{m}} \right)$ để phục vụ sản xuất. Giả thiết chất lượng và thời gian khoan giếng của hai cơ sở là như nhau. Công ty ấy nên chọn cơ sở nào để tiết kiệm chi phí nhất?
Trong kì thi học sinh giỏi có 10 học sinh đạt tối đa điểm môn Toán trong đó có 4 học sinh nam và 6 học sinh nữ. Nhà trường muốn chọn một nhóm 5 học sinh trong 10 học sinh trên để tham dự buổi lễ tuyên dương khen thưởng. Tính số cách chọn một nhóm gồm 5 học sinh mà có cả nam và nữ và số học sinh nam ít hơn số học sinh nữ.
Đáp án:
Đáp án:
Có \(60\) quả cầu được đánh số từ \(1\) đến \(60.\) Lấy ngẫu nhiên đồng thời hai quả cầu rồi nhân các số trên hai quả cầu với nhau. Tính xác suất để tích nhận được là số chia hết cho \(10.\)
Cho đa thức \(f\left( x \right)\) thỏa mãn \(\mathop {\lim }\limits_{x \to 1} \dfrac{{f\left( x \right) - 2}}{{x - 1}} = 12\). Tính \(\mathop {\lim }\limits_{x \to 1} \dfrac{{f\left( x \right) - 2}}{{\left( {{x^2} - 1} \right)\left[ {f\left( x \right) + 1} \right]}} \)
Đáp án: \(\mathop {\lim }\limits_{x \to 1} \dfrac{{f\left( x \right) - 2}}{{\left( {{x^2} - 1} \right)\left[ {f\left( x \right) + 1} \right]}} \)
Đáp án: \(\mathop {\lim }\limits_{x \to 1} \dfrac{{f\left( x \right) - 2}}{{\left( {{x^2} - 1} \right)\left[ {f\left( x \right) + 1} \right]}} \)
Cho hàm số \(f\left( x \right) = \left( {x - 2} \right)\sqrt {{x^2} - 1} \), tìm tập nghiệm S của bất phương trình \(f'\left( x \right) \le \sqrt {{x^2} - 1} \)
Cho tứ diện \(ABCD\). Gọi \(M,\,N\)lần lượt là trung điểm của các cạnh \(AB\), \(CD\). \(G\)là trung điểm của \(MN\), \(I\)là giao điểm của đường thẳng \(AG\)và mặt phẳng \(\left( {BCD} \right)\). Tính tỉ số \(\dfrac{{GI}}{{GA}}\)?
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AA' = a,\)\(AD = a\sqrt 3 \). Góc giữa hai mặt phẳng \(\left( {ABC'D'} \right)\) và \(\left( {ABCD} \right)\) bằng:
Đáp án:
$^0$
Đáp án:
$^0$
Giả sử \(F\left( x \right) = \left( {a{x^2} + bx + c} \right){e^x}\) là một nguyên hàm của hàm số \(f\left( x \right) = {x^2}{e^x}\). Tính tích \(P = abc\).
Vòm cửa lớn của một trung tâm văn hóa có hình parabol. Gắn parabol vào hệ trục \(Oxy\) thì nó có đỉnh \(\left( {0;8} \right)\) và cắt trục hoành tại 2 điểm phân biệt, trong đó có 1 điểm là \(\left( { - 4;0} \right)\). Người ta dự định lắp vào cửa kính cho vòm cửa này. Hãy tính diện tích mặt kính cần lắp vào.
Biết hàm số \(y = f\left( x \right)\) liên tục và có đạo hàm trên \(\left[ {0;\,\,2} \right],\)\(f\left( 0 \right) = \sqrt 5 ,\)\(f\left( 2 \right) = \sqrt {11} .\) Tích phân \(I = \int\limits_0^2 {f\left( x \right).f'\left( x \right)dx} \) bằng:
Biết \(\int\limits_{0}^{1}{3{{e}^{\sqrt{3x+1}}}dx}=\frac{a}{5}{{e}^{2}}+\frac{b}{3}e+c\,\,\left( a,b,c\in Q \right)\) . Tính \(P=a+b+C\)
Gọi $V$ là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường \(y = \sqrt x ,y = 0\) và $x = 4$ quanh trục $Ox$ . Đường thẳng \(x = a(0 < a < 4)\) cắt đồ thị hàm số \(y = \sqrt x \) tại $M$ (hình vẽ bên).
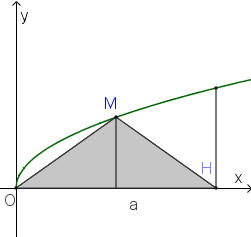
Gọi ${V_1}$ là thể tích khối tròn tạo thành khi quay quanh tam giác $OMH$ quanh trục $Ox$. Biết rằng \(V = 2{V_1}\) . Khi đó:
Bạn Lan muốn có $10.000.000$ sau $15$ tháng thì mỗi tháng phải gửi vào ngân hàng bao nhiêu tiền, biết lãi suất ngân hàng là $0,6\% $ mỗi tháng.
Số nghiệm nguyên của bất phương trình \({4^x} - {5.2^x} + 4 < 0\) là:
Tập nghiệm của bất phương trình $2017{\log _2}x \le {4^{{{\log }_2}9}}$ là
Tìm nghiệm của phương trình \({9^{\sqrt {x - 1} }} = {e^{\ln 81}}\)
Giải phương trình $\log_{3}\left( {2x-1} \right) = 2$ , ta có nghiệm là:
Tìm tất cả các giá trị của tham số $m$ để hàm số $y = {x^3} - 2m{x^2} + {m^2}x + 2$ đạt cực tiểu tại $x=1$.
Tập hợp các giá trị của tham số \(m\) để hàm số \(y = 2{x^2} - mx + m\) đồng biến trên khoảng \(\left( {1; + \infty } \right)\) là
Cho khối chóp S.ABC có các góc phẳng ở đỉnh S bằng \(60^\circ ,SA = 1,SB = 2,SC = 3\). Thể tích của khối chóp S.ABC bằng
Tính tổng phần thực của tất cả các số phức \(z \ne 0\) thỏa mãn \(\left( {z + \dfrac{5}{{\left| z \right|}}} \right)i = 7 - z.\)
Cho ba điểm $A,B,C$ lần lượt biểu diễn các số phức sau \({z_1} = 1 + i;\,{z_2} = {z_1}^2;\,{z_3} = m - i\). Tìm các giá trị thực của $m$ sao cho tam giác $ABC$ vuông tại $B$.
Trong mặt phẳng tọa độ, tập hợp các điểm M biểu diễn của số phức z thỏa mãn\(\left| {z + 1 + 3i} \right| = \left| {z - 2 - i} \right|\) là phương trình đường thẳng có dạng \(ax+by+c=0\). Khi đó tỉ số \(\dfrac{a}{b}\) bằng:
Đáp án:
Đáp án:
Gọi \(A,B\) lần lượt là điểm biểu diễn cho hai số phức \({z_1} = 1 + i\) và \({z_2} = 1 - 3i.\) Gọi M là trung điểm của AB. Khi đó M là điểm biểu diễn cho số phức nào dưới đây ?
Viết phương trình mặt phẳng $\left( P \right)$ đi qua điểm $M\left( {1;0; - 2} \right)$ và vuông góc với hai mặt phẳng $\left( Q \right),\left( R \right)$ cho trước với $\left( Q \right):x + 2y - 3z + 1 = 0$ và $\left( {{\rm{ }}R} \right):2x - 3y + z + 1 = 0$ .
Trong không gian Oxyz, cho mặt phẳng \(\left( P \right):x - 3y + 2z - 5 = 0\) và hai điểm \(A\left( {2;4;1} \right)\),\(B\left( { - 1;1;3} \right)\). Viết phương trình mặt phẳng \(\left( Q \right)\) đi qua hai điểm \(A,\,\,B\) và vuông góc với mặt phẳng \(\left( P \right)\).
Hình chiếu của điểm \(M\left( {1; - 1;0} \right)\) lên trục ${\rm{O}}z$ là:
Trong không gian Oxyz, cho 3 điểm \(A\left( {0;1;1} \right),{\mkern 1mu} B\left( {3;0; - 1} \right),{\mkern 1mu} C\left( {0;21; - 19} \right)\) và mặt cầu \(\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 1} \right)^2} = 1\). Điểm M thuộc mặt cầu (S) sao cho tổng \(3M{A^2} + 2M{B^2} + M{C^2}\) đạt giá trị nhỏ nhất, khi đó, độ dài vectơ \(\overrightarrow {OM} \) là
Trong không gian với hệ tọa độ \(Oxyz\), cho mặt phẳng \(\left( P \right):x + 2y - 3z + 4 = 0\) và đường thẳng \(d:\dfrac{{x + 2}}{1} = \dfrac{{y - 2}}{1} = \dfrac{z}{{ - 1}}\). Đường thẳng \(\Delta \) nằm trong \(\left( P \right)\) đồng thời cắt và vuông góc với \(d\) có phương trình:
Trong không gian với hệ trục tọa độ $Oxyz$, cho hình hộp $ABCD.A'B'C'D'$ biết $A\left( {1;0;1} \right)$, $~B\left( 2;1;2 \right)$, $D\left( {1; - 1;1} \right)$ và \(C'(4;5; - 5)\). Khi đó, thể tích của hình hộp đó là:
Trong không gian Oxyz, cho điểm \(M\left( {1;\,\,2;\,\,4} \right)\) và mặt phẳng \(\left( P \right):\,\,x + 2y - 2z + 5 = 0.\) Khoảng cách từ điểm \(M\) đến mặt phẳng \(\left( P \right)\) có dạng $\dfrac{a}{b}$ với $\dfrac{a}{b}$ là phân số tối giản. Tính $a+b$
Đáp án:
Đáp án:
Trong không gian với hệ tọa độ Oxyz, điểm $A’(a;b;c)$ đối xứng với điểm \(A\left( { - 1;0;3} \right)\) qua mặt phẳng \(\left( P \right):x + 3y - 2z - 7 = 0\). Tìm $a+b+c$
Đáp án:
Đáp án:
Trong không gian \(Oxyz,\) cho tam giác \(ABC\) có \(A\left( {1;\,\,2;\,\,1} \right),\,\,\,B\left( {1;\,\,0;\,\,1} \right)\) và \(C\left( {1;\,\,1;\,\,2} \right).\) Diện tích tam giác \(ABC\) bằng:
Cho hình chóp \(S.ABCD\) có \(ABCD\) là hình thang vuông tại \(A\) và \(D\) thỏa mãn \(SA \bot \left( {ABCD} \right)\) và \(AB = 2AD = 2CD = 2a = \sqrt 2 SA\). Thể tích khối chóp \(S.BCD\) là:
Tìm $m$ để hàm số $y = {x^3} - 3{x^2} + mx + 2$ tăng trên khoảng $\left( {1; + \infty {\rm{\;}}} \right).$
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
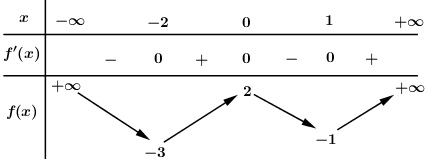
Số điểm cực tiểu của hàm số \(g\left( x \right) = {f^3}\left( x \right) - 3f\left( x \right)\) là:
Cho hàm số \(f\left( x \right)\) có đạo hàm \(f'\left( x \right) = {x^2}\left( {x + 2} \right)\left( {x - 3} \right)\). Điểm cực đại của hàm số \(g\left( x \right) = f\left( {{x^2} - 2x} \right)\) là:
Hàm số \(f\left( x \right) = \left| {\dfrac{x}{{{x^2} + 1}} - m} \right|\) (với \(m\) là tham số thực) có nhiều nhất bao nhiêu điểm cực trị?
Cho hình chóp S.ABC có \(SA = SB = SC = a\sqrt {3},\) \(AB = AC = 2a,BC = 3a\). Thể tích khối chóp S.ABC bằng:
Cho hàm số $y = \dfrac{{2x - 1}}{{x - 1}}\,\,\,\left( C \right)$. Tìm điểm $M$ thuộc $(C)$ sao cho tiếp tuyến tại $M$ và hai trục tọa độ tạo thành tam giác cân.
Xét các số thực \(x,y\) thỏa mãn \({2^{{x^2} + {y^2} + 1}} \le \left( {{x^2} + {y^2} - 2x + 2} \right){4^x}\). Giá trị lớn nhất của biểu thức \(P = \dfrac{{8x + 4}}{{2x - y + 1}}\) là $a+\sqrt{a}$
Tìm $a$
Đáp án:
Đáp án:
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ dưới đây. Tập hợp tất cả các giá trị thực của tham số \(m\) để phương trình \(f\left( {\sqrt {4 - {x^2}} } \right) = m\) có nghiệm thuộc nửa khoảng \(\left[ { - \sqrt 2 ;\sqrt 3 } \right)\) là
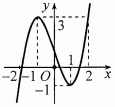
Đáp án:
Đáp án:

