Trong không gian Oxyz, cho 3 điểm \(A\left( {0;1;1} \right),{\mkern 1mu} B\left( {3;0; - 1} \right),{\mkern 1mu} C\left( {0;21; - 19} \right)\) và mặt cầu \(\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 1} \right)^2} = 1\). Điểm M thuộc mặt cầu (S) sao cho tổng \(3M{A^2} + 2M{B^2} + M{C^2}\) đạt giá trị nhỏ nhất, khi đó, độ dài vectơ \(\overrightarrow {OM} \) là
Trả lời bởi giáo viên
+) Mặt cầu \(\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 1} \right)^2} = 1\) có tâm \(J\left( {1;1;1} \right)\), bán kính \(R = 1\).
+) Tìm \(I\):
\(3\overrightarrow {IA} + 2\overrightarrow {IB} + \overrightarrow {IC} = \vec 0 \) \(\Leftrightarrow 6\overrightarrow {IA} + 2\overrightarrow {AB} + \overrightarrow {AC} = \vec 0 \) \(\Leftrightarrow \overrightarrow {IA} = - \dfrac{{2\overrightarrow {AB} + \overrightarrow {AC} }}{6}\)
\(A\left( {0;1;1} \right),{\mkern 1mu} B\left( {3;0; - 1} \right),{\mkern 1mu} C\left( {0;21; - 19} \right) \) \(\Rightarrow \overrightarrow {IA} \left( { - {x_I};1 - {y_I};1 - {z_I}} \right),{\mkern 1mu} {\mkern 1mu} \overrightarrow {AB} \left( {3; - 1; - 2} \right),\) \({\mkern 1mu} {\mkern 1mu} \overrightarrow {AC} \left( {0;20; - 20} \right)\)
\( \Rightarrow \left\{ \begin{array}{l} - {x_I} = - \dfrac{{2.3 + 0}}{6}\\1 - {y_I} = - \dfrac{{2.\left( { - 1} \right) + 20}}{6}\\1 - {z_I} = - \dfrac{{2.\left( { - 2} \right) + \left( { - 20} \right)}}{6}\end{array} \right.\) \( \Rightarrow I\left( {1;4; - 3} \right)\)
+) Ta có:
\(\begin{array}{l}3M{A^2} + 2M{B^2} + M{C^2} \\= 3{\left( {\overrightarrow {MI} + \overrightarrow {IA} } \right)^2} + 2{\left( {\overrightarrow {MI} + \overrightarrow {IB} } \right)^2} + {\left( {\overrightarrow {MI} + \overrightarrow {IC} } \right)^2}\\ = 6M{I^2} + 3I{A^2} + 2I{B^2} + I{C^2} \\+ 2.\overrightarrow {MI} .\left( {3\overrightarrow {IA} + 2\overrightarrow {IB} + \overrightarrow {IC} } \right) \\= 6M{I^2} + 3I{A^2} + 2I{B^2} + I{C^2} + 2.\overrightarrow {MI} .\vec 0\\ = 6M{I^2} + 3I{A^2} + 2I{B^2} + I{C^2}\end{array}\)
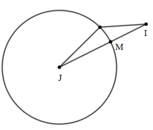
Để tổng trên là nhỏ nhất thì MI nhỏ nhất \( \Rightarrow M\) là giao điểm của đoạn thẳng IJ và mặt cầu \(\left( S \right)\).
\(\overrightarrow {JI} = \left( {0;3; - 4} \right)\)\( \Rightarrow \) Tọa độ điểm \(M\) thuộc đoạn IJ có dạng \(\left( {1;1 + 3t;1 - 4t} \right),{\mkern 1mu} {\mkern 1mu} t \in \left[ {0;1} \right]\)
Mặt khác \(M \in \left( S \right) \) \(\Rightarrow {\left( {1 - 1} \right)^2} + {\left( {1 - \left( {1 + 3t} \right)} \right)^2} + {\left( {1 - \left( {1 - 4t} \right)} \right)^2} = 1\)
\( \Leftrightarrow {t^2} = \dfrac{1}{{25}} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\rm{\;}}&{t = \dfrac{1}{5}}\\{}&{t = - \dfrac{1}{5}{\mkern 1mu} (L)}\end{array}} \right. \Leftrightarrow t = \dfrac{1}{5}\)\( \Rightarrow M\left( {1;\dfrac{8}{5};\dfrac{1}{5}} \right) \Rightarrow OM = \dfrac{{3\sqrt {10} }}{5}\).
Hướng dẫn giải:
- Tìm tọa độ điểm \(I\) sao cho \(3\overrightarrow {IA} + 2\overrightarrow {IB} + \overrightarrow {IC} = \vec 0\).
- Biến đổi \(3M{A^2} + 2M{B^2} + M{C^2}\) qua dạng vecto và đánh giá giá trị nhỏ nhất của tổng.
Giải thích thêm:
M(1;1+3t;1-4t) thuộc đoạn IJ nếu \(t\in [0;1]\) vì:
\(\overrightarrow {MI} = \left( {0; - 3 + 3t;4 - 4t} \right),\)\(\overrightarrow {MJ} = \left( {0;3t; - 4t} \right)\)
\(\overrightarrow {MI} = k\overrightarrow {MJ} \left( {k < 0} \right) \Rightarrow \left\{ \begin{array}{l} - 3 + 3t = k.3t\\4 - 4t = k.\left( { - 4t} \right)\end{array} \right.\)\( \Leftrightarrow 1 - t = - kt \Leftrightarrow 1 = \left( {1 - k} \right)t\)\( \Leftrightarrow t = \frac{1}{{1 - k}}\)
Do \(k < 0\) nên \(1 - k > 1 \Rightarrow \frac{1}{{1 - k}} < 1\) và \(\frac{1}{{1 - k}} > 0\) hay \(0 < t < 1\).
Ngoài ra t = 0 hoặc t = 1 khi M trùng các điểm đầu mút.
Vậy \(t\in [0;1]\).
Chú ý:
Các em cũng không cần đặt điều kiện \(t\in [0;1]\), khi không đặt đk thì sau khi tìm được hai giá trị của t, thay hai giá trị này tìm hai điểm M. Tính độ dài mỗi đoạn MI có được và so sánh, đoạn nào ngắn hơn ta sẽ nhận điểm M đó.