Đề thi tư duy định lượng - Đề số 1
Kỳ thi ĐGNL ĐHQG Hà Nội
Kết quả:
0/50
Thời gian làm bài: 00:00:00
Các hành vi không khai báo, khai báo không trung thực hoặc che giấu hiện trạng bệnh của bản thân hoặc người khác mắc bệnh truyền nhiễm nhóm A đều bị xử phạt theo quy định của pháp luật.

Hành vi nào sau đây có mực xử phạt hành chính cao nhất:
Một chất điểm chuyển động theo phương trình \(S = - \dfrac{1}{3}{t^3} + 6{t^2}\), trong đó \(t > 0,t\) được tính bằng giây \((s)\) và \(S\) tính bằng mét \((m)\). Vận tốc của chất điểm tại thời điểm \(t = 3\) (giây) bằng
Tìm tập nghiệm của phương trình \({\log _3}x + \dfrac{1}{{{{\log }_9}x}} = 3\)
Hệ \(\left\{ \begin{array}{l}x - y = 5\\{x^2} - {y^2} = 15\end{array} \right.\) có nghiệm là
Gọi \(A\) và \(B\) lần lượt là điểm biểu diễn của số phức \({z_1} = 3 - 2i\) và \({z_2} = 1 + 4i\). Trung điểm của đoạn thẳng \(AB\) có tọa độ là:
Trong không gian với hệ trục tọa độ \({\mathop{\rm Oxyz}\nolimits} \), cho điểm \(A(4; - 3;5)\) và \(B(2; - 5;1).\)Viết phương trình mặt phẳng \((P)\) đi qua trung điểm \(I\) của đoạn thẳng \(AB\) và vuông góc với đường thẳng \((d):\dfrac{{x + 1}}{3} = \dfrac{{y - 5}}{{ - 2}} = \dfrac{{z + 9}}{{13}}\).
Khi chiếu điểm \(M\left( { - 4;3; - 2} \right)\) lên trục ${\rm{Ox}}$ được điểm \(N\) thì:
Tập nghiệm \(S\) của hệ bất phương trình $\left\{ \begin{array}{l}\dfrac{{2x - 1}}{3} > - x + 1\\\dfrac{{4 - 3x}}{2} < 3 - x\end{array} \right.$ là:
Phương trình \(\cos 11x\cos 3x = \cos 17x\cos 9x\) có nghiệm là:
Mặt sàn tầng một của một ngôi nhà cao hơn mặt sân $0,5m$. Cầu thang đi từ tầng một lên tầng hai gồm $21$ bậc, mỗi bậc cao $18cm$. Ký hiệu ${h_n}$ là độ cao của bậc thứ $n$ so với mặt sân. Viết công thức để tìm độ cao ${h_n}$.
Hàm số nào không là nguyên hàm của hàm số \(y = 3{x^4}\)?
Cho hàm số \(f\left( x \right)\) có bảng biến thiên như hình vẽ:
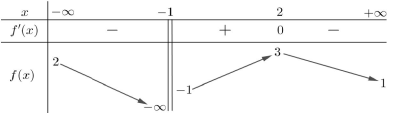
Tìm điều kiện của tham số \(m\) để \(m < f\left( x \right) + {x^2}\) với mọi \(x \in \left( {1;2} \right)\).
Một chất điểm chuyển động thẳng với vận tốc\(v\left( t \right) = 2t + 3\,\left( {m/s} \right)\), với \(t\) là thời gian tính bằng giây \(\left( s \right)\) từ lúc chất điểm bắt đầu chuyển động. Tính quãng đường chất điểm đi được trong khoảng thời gian từ giây thứ nhất đến giây thứ năm.
Một thiết bị trong năm 2021 được định giá 100 triệu đồng. Trong 5 năm tiếp theo, mỗi năm giá trị thiết bị giảm 6 % so với năm trước và từ năm thứ 6 trở đi, mỗi năm giá trị thiết bị giảm 10 % so với năm trước. Hỏi bắt đầu từ năm nào thì giá trị thiết bị nhỏ hơn 50 triệu đồng?
Số nghiệm thực phân biệt của phương trình ${4^{{x^2}}} - {5.2^{{x^2}}} + 4 = 0$ là
Gọi \(\left( {{D_1}} \right)\) là hình phẳng giới hạn bởi các đường \(y = 2\sqrt x ,\,\,y = 0\) và \(x = 2020,\) \(\left( {{D_2}} \right)\) là hình phẳng giới hạn bởi các đường \(y = \sqrt {3 x},\,\,y = 0\) và \(x = 2020.\) Gọi \({V_1},\,\,{V_2}\) lần lượt là thể tích khối tròn xoay tạo thành khi quay \(\left( {{D_1}} \right)\) và \(\left( {{D_2}} \right)\) xung quanh trục \(Ox.\) Tỉ số \(\dfrac{{{V_1}}}{{{V_2}}}\) bằng:
Tìm $m$ để hàm số $y = \dfrac{{{x^3}}}{3} - 2m{x^2} + 4mx + 2$ nghịch biến trên khoảng $\left( { - 2;0} \right)$.
Tìm môđun của số phức \(z\), biết \(\dfrac{1}{{{z^2}}} = \dfrac{1}{2} + \dfrac{1}{2}i.\)
Tìm tập hợp các điểm biểu diễn số phức \(z\), biết rằng số phức \({z^2}\) có điểm biểu diễn nằm trên trục tung.
Trong mặt phẳng với hệ trục tọa độ Oxy, cho đường thẳng \(\left( d \right):3x - 4y - 12 = 0\). Phương trình đường thẳng \(\left( \Delta \right)\) đi qua \(M\left( {2; - 1} \right)\) và tạo với \(\left( d \right)\) một góc \({45^o}\) có dạng \(ax + by + 5 = 0\), trong đó a,b cùng dấu. Khẳng định nào sau đây đúng?
Trong mặt phẳng với hệ tọa độ \(Oxy\), cho đường tròn \(({C_m}):{x^2} + {y^2} - 2mx - 4my - 5 = 0\) (\(m\) là tham số). Biết đường tròn \(({C_m})\) có bán kính bằng 5. Khi đó tập hợp tất cả các giá trị của \(m\) là
Trong không gian với hệ tọa độ $Oxyz$, cho mặt phẳng $\left( P \right):ax + by + cz - 27 = 0$ qua hai điểm $A\left( {3,2,1} \right),B\left( { - 3,5,2} \right)$ và vuông góc với mặt phẳng $\left( Q \right):3x + y + z + 4 = 0$ . Tính tổng $S = a + b + c$.
Trong không gian \(Oxyz\), cho hai điểm \(A\left( {1;0;2} \right)\), \(B\left( {2; - 1;3} \right)\). Số điểm \(M\) thuộc trục \(Oy\) sao cho tam giác \(MAB\) có diện tích bằng \(\dfrac{{\sqrt 6 }}{4}\) là:
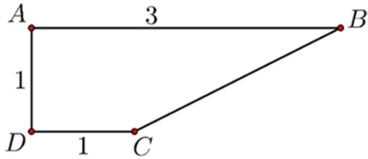
Cho hình thang ABCD vuông tại A và D, có AB=3, DC=AD=1. Thể tích của khối tròn xoay nhận được khi quay hình thang ABCD quang trục AB là
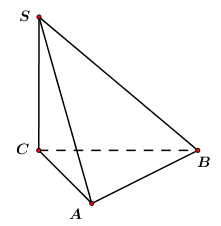
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(A,\,\,BC = 2AB = 2a.\) Cạnh bên \(SC\) vuông góc với đáy, góc giữa \(SA\) và đáy bằng \({60^0}.\) Thể tích khối chóp đó bằng:
Cho hình chóp $S.ABCD$ có đáy $ABCD $ là hình bình hành. \(Mp\left( \alpha \right)\) qua $BD$ và song song với $SA$ cắt $SC$ tại $K.$ Chọn khẳng định đúng?
Trong không gian với hệ tọa độ \(Oxyz\), cho mặt cầu \(\left( S \right):\,\,{x^2} + {y^2} + {z^2} - 8x + 2y + 2z - 3 = 0\) và đường thẳng \(\Delta :\,\,\dfrac{{x - 1}}{3} = \dfrac{y}{{ - 2}} = \dfrac{{z + 2}}{{ - 1}}\). Mặt phẳng \(\left( \alpha \right)\) vuông góc với \(\Delta \) và cắt \(\left( S \right)\) theo giao tuyến là đường tròn \(\left( C \right)\) có bán kính lớn nhất. Phương trình \(\left( \alpha \right)\) là:
Trong không gian \(Oxyz,\) gọi \(d'\) là hình chiếu vuông góc của đường thẳng \(d:\,\,\left\{ \begin{array}{l}x = t\\y = t\\z = t\end{array} \right.\) trên mặt phẳng \(\left( {Oxy} \right)\). Phương trình tham số của đường thẳng \(d'\) là
Cho hàm số \(f\left( x \right)\) có đạo hàm \(f'\left( x \right) = {x^2}\left( {x + 2} \right)\left( {x - 3} \right)\). Điểm cực đại của hàm số \(g\left( x \right) = f\left( {{x^2} - 2x} \right)\) là:
Trong không gian \(Oxyz,\) cho hai điểm \(A\left( {4;0;4} \right)\) và \(B\left( {2;4;0} \right)\). Điểm \(M\) di động trên tia \(Oz\), điểm \(N\) di động trên tia \(Oy\). Đường gấp khúc \(AMNB\) có độ dài nhỏ nhất bằng bao nhiêu? (Kết quả làm tròn đến hàng phần chục).
Cho hàm số \(f\left( x \right) = \dfrac{1}{3}{x^3} + m{x^2} + \left( {{m^2} - 4} \right)x + 1\). Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y = f\left( {\left| x \right|} \right)\) có đúng 3 điểm cực trị?
Đổi biến $u = \ln x$ thì tích phân \(I = \int\limits_1^e {\dfrac{{1 - \ln x}}{{{x^2}}}dx} \) thành:
Một hộp đựng 8 quả cầu xanh, 12 quả cầu đỏ. Lấy ngẫu nhiên 1 quả cầu trong hộp, sau đó lấy ngẫu nhiên một quả cầu trong các quả cầu còn lại. Xác suất để lấy được 2 quả cầu cùng màu là:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân đỉnh B, \(AB = 4,SA = SB = SC = 12\). Gọi M, N, E lần lượt là trung điểm AC, BC, AB. Trên cạnh SB lấy điểm F sao cho \(\dfrac{{BF}}{{BS}} = \dfrac{2}{3}\). Thể tích khối tứ diện \(MNEF\) bằng
Một lớp 11 có 30 học sinh, gồm 15 nam và 15 nữ. Gọi a là số cách xếp các học sinh thành hai hàng, một hàng nam và một hàng nữ trong lúc tập thể dục giữa giờ. Tính a.
Đáp án:
$^2$
Đáp án:
$^2$
Trong không gian \(Oxyz\), cho mặt phẳng \(\left( P \right):\,2x + 2y + z - 1 = 0\). Khoảng cách từ gốc tọa độ \(O\) đến mặt phẳng \(\left( P \right)\) bằng bao nhiêu?
Đáp án:
Đáp án:
Hàm số \(f\left( x \right) = {x^4}{\left( {x - 1} \right)^2}\) có bao nhiêu điểm cực trị?
Đáp án
Đáp án
Cho hàm số \(y = \dfrac{{x + 2}}{{x - 1}}\) có đồ thị là \(\left( C \right)\) tại điểm \(M\left( {2;4} \right)\) có hệ số góc bằng bao nhiêu?
Đáp án:
Đáp án:
Khi xây nhà, cô Ngọc cần xây một bể đựng nước mưa có thể tích \(V = 6{m^3}\) dạng hình hộp chữ nhật với chiều dài gấp ba lần chiều rộng, đáy và nắp và các mặt xung quanh đều được đổ bê tông cốt thép. Phần nắp bể để hở một khoảng hình vuông có diện tích bằng \(\dfrac{2}{9}\) diện tích nắp bể. Biết rằng chi phí cho \(1{m^2}\) bê tông cốt thép là \(1.000.000d\). Tính chi phí thấp nhất mà cô Ngọc phải trả khi xây bể (làm tròn đến hàng trăm nghìn và các chữ số viết liền)?
Đáp án
VNĐ
Đáp án
VNĐ
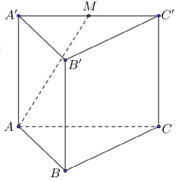
Cho hình lăng trụ tam giác đều \(ABC.A'B'C'\) có độ dài cạnh đáy \(AB = 8,\) cạnh bên bằng \(\sqrt 6 \) (minh họa như hình vẽ). Gọi \(M\) là trung điểm của cạnh \(A'C'\). Khoảng cách từ \(B'\) đến mặt phẳng \(\left( {ABM} \right)\) bằng bao nhiêu?
Đáp án: $d\left(B^{\prime},(A B M)\right)$
Đáp án: $d\left(B^{\prime},(A B M)\right)$
Cho phương trình \({11^x} + m = {\log _{11}}\left( {x - m} \right)\) với \(m\) là tham số. Có bao nhiêu giá trị nguyên của \(m \in \left( { - 205;205} \right)\) để phương trình đã cho có nghiệm?
Đáp án
Đáp án
Trong không gian \(Oxyz,\) gọi \(M'\) là điểm đối xứng của điểm \(M\left( {2;0;1} \right)\) qua đường thẳng \(\Delta :\,\,\,\dfrac{x}{1} = \dfrac{{y + 2}}{2} = \dfrac{{z - 1}}{1}\). Tính khoảng cách từ điểm \(M'\) đến mặt phẳng \(\left( {Oxy} \right).\)
Đáp án
Đáp án
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân, \(AB = BC = 2a\). Tam giác \(SAC\) cân tại \(S\) và nằm trong mặt phẳng vuông góc với \(\left( {ABC} \right)\), \(SA = \sqrt 3 a\). Góc giữa hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SAC} \right)\) bằng:
Đáp án
$^0$
Đáp án
$^0$
Biết rằng tập hợp điểm biểu diễn các số phức \(z\) thỏa mãn \(\left| {\left( {1 + i} \right)z + 5 - i} \right| = 1\) là đường tròn tâm \(I\left( {a;b} \right)\). Tính \(a + b.\)
Đáp án
Đáp án
Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị như hình vẽ bên dưới.
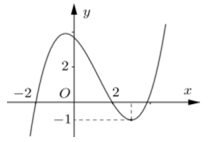
Số nghiệm thực của phương trình \(\left| {f\left( {{x^3} - 3x} \right)} \right| = \dfrac{2}{3}\) là
Đáp án
Đáp án
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Biết các miền \(A\) và \(B\) có diện tích lần lượt là 4 và 1. Tính \(\int\limits_1^2 {4xf\left( {{x^2}} \right)d{\rm{x}}} \)
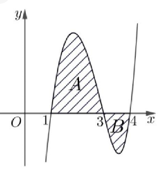
Đáp án: \(\int\limits_1^2 {4xf\left( {{x^2}} \right)d{\rm{x}}} \)
Đáp án: \(\int\limits_1^2 {4xf\left( {{x^2}} \right)d{\rm{x}}} \)
Gọi k là số các giá trị nguyên của tham số \(m\) trên đoạn [-5;5] để hàm số \(y = \dfrac{{ - {x^3}}}{3} + m{x^2} - 2mx + 1\) có hai điểm cực trị. Tìm k.
Đáp án:
Đáp án:
Một vật được ném lên trên cao và độ cao của nó so với mặt đất được cho bởi công thức \(h\left( t \right) = 3 + 10t - 2{t^2}\left( m \right)\), với \(t\) là thời gian tính bằng giây \(\left( s \right)\) kể từ lúc bắt đầu ném. Độ cao cực đại mà vật đó có thể đạt được so với mặt đất bằng bao nhiêu mét?
Đáp án:
Đáp án:
Cho đa thức \(f\left( x \right)\) thỏa mãn \(\mathop {\lim }\limits_{x \to 1} \dfrac{{f\left( x \right) - 2}}{{x - 1}} = 12\). Tính \(\mathop {\lim }\limits_{x \to 1} \dfrac{{f\left( x \right) - 2}}{{\left( {{x^2} - 1} \right)\left[ {f\left( x \right) + 1} \right]}} \)
Đáp án: \(\mathop {\lim }\limits_{x \to 1} \dfrac{{f\left( x \right) - 2}}{{\left( {{x^2} - 1} \right)\left[ {f\left( x \right) + 1} \right]}} \)
Đáp án: \(\mathop {\lim }\limits_{x \to 1} \dfrac{{f\left( x \right) - 2}}{{\left( {{x^2} - 1} \right)\left[ {f\left( x \right) + 1} \right]}} \)

