Cho hình lăng trụ tam giác đều \(ABC.A'B'C'\) có độ dài cạnh đáy \(AB = 8,\) cạnh bên bằng \(\sqrt 6 \) (minh họa như hình vẽ). Gọi \(M\) là trung điểm của cạnh \(A'C'\). Khoảng cách từ \(B'\) đến mặt phẳng \(\left( {ABM} \right)\) bằng bao nhiêu?
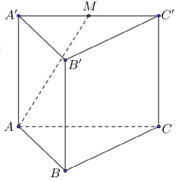
Đáp án: $d\left(B^{\prime},(A B M)\right)$
Trả lời bởi giáo viên
Đáp án: $d\left(B^{\prime},(A B M)\right)$
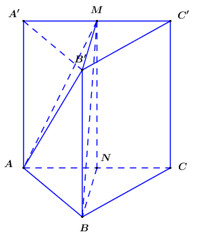
Bước 1: Gọi \(N\) là trung điểm của \(AC\), chứng minh \(d\left( {A;\left( {BB'M} \right)} \right) = d\left( {A;\left( {BB'MN} \right)} \right) = AN\).
Gọi \(N\) là trung điểm của \(AC\) ta có \(\left( {BB'M} \right) \equiv \left( {BB'MN} \right)\) nên \(d\left( {A;\left( {BB'M} \right)} \right) = d\left( {A;\left( {BB'MN} \right)} \right)\).
Vì tam giác ABC đều nên \(AN \bot BN\). Ta có \(\left\{ \begin{array}{l}AN \bot BN\\AN \bot MN\end{array} \right. \Rightarrow AN \bot \left( {BB'MN} \right)\) nên \(d\left( {A;\left( {BB'MN} \right)} \right) = AN = 4\)
Bước 2: Tính \({V_{A.BB'M}} = \dfrac{1}{3}d\left( {A;\left( {BB'MN} \right)} \right).{S_{\Delta BB'M}} = {V_{B'.ABM}}\).
Ta lại có \(BN = \dfrac{{AB\sqrt 3 }}{2} = 4\sqrt 3 ,\,\,MN = AA' = \sqrt 6 \) nên \({S_{BB'MN}} = MN.BN = \sqrt 6 .4\sqrt 3 = 12\sqrt 2 \) \( \Rightarrow {S_{\Delta BB'M}} = 6\sqrt 2 \).
\( \Rightarrow {V_{A.BB'M}} = \dfrac{1}{3}d\left( {A;\left( {BB'MN} \right)} \right).{S_{\Delta BB'M}} = \dfrac{1}{3}.4.12\sqrt 2 = 16\sqrt 2 = {V_{B'.ABM}}\)
Bước 3: Sử dụng \(d\left( {B';\left( {ABM} \right)} \right) = \dfrac{{3{V_{B'.ABM}}}}{{{S_{\Delta ABM}}}}\).
Lại có \({V_{B'.ABM}} = \dfrac{1}{3}d\left( {B';\left( {ABM} \right)} \right).{S_{\Delta ABM}}\) nên \(d\left( {B';\left( {ABM} \right)} \right) \)\(= \dfrac{{3{V_{B'.ABM}}}}{{{S_{\Delta ABM}}}}\).
Ta có:
\(\begin{array}{l}AM = \sqrt {A'{A^2} + A'{M^2}} \\= \sqrt {{{\left( {\sqrt 6 } \right)}^2} + {4^2}} = \sqrt {22} \\AB = 8\\BM = \sqrt {BB{'^2} + B'{M^2}} \\= \sqrt {{{\left( {\sqrt 6 } \right)}^2} + {{\left( {4\sqrt 3 } \right)}^2}} = 3\sqrt 6 \end{array}\)
Bước 4: Sử dụng công thức \({S_{\Delta ABM}} = \sqrt {p\left( {p - AM} \right)\left( {p - AB} \right)\left( {p - BM} \right)} \) với \(p\) là nửa chu vi tam giác \(ABM\).
Gọi \(p\) là nửa chu vi tam giác ABM ta có \(p = \dfrac{{\sqrt {22} + 8 + 3\sqrt 6 }}{2}\).
\( \Rightarrow {S_{\Delta ABM}} \)\(= \sqrt {p\left( {p - AM} \right)\left( {p - AB} \right)\left( {p - BM} \right)} \)\( = 12\sqrt 2 \)
Vậy \(d\left( {B';\left( {ABM} \right)} \right) = \dfrac{{3{V_{B'.ABM}}}}{{{S_{\Delta ABM}}}} = \dfrac{{3.16\sqrt 2 }}{{12\sqrt 2 }} = 4\).
Hướng dẫn giải:
Bước 1: Gọi \(N\) là trung điểm của \(AC\), chứng minh \(d\left( {A;\left( {BB'M} \right)} \right) = d\left( {A;\left( {BB'MN} \right)} \right) = AN\).
Bước 2: Tính \({V_{A.BB'M}} = \dfrac{1}{3}d\left( {A;\left( {BB'MN} \right)} \right).{S_{\Delta BB'M}} = {V_{B'.ABM}}\).
Bước 3: Sử dụng \(d\left( {B';\left( {ABM} \right)} \right) = \dfrac{{3{V_{B'.ABM}}}}{{{S_{\Delta ABM}}}}\).
Bước 4: Sử dụng công thức \({S_{\Delta ABM}} = \sqrt {p\left( {p - AM} \right)\left( {p - AB} \right)\left( {p - BM} \right)} \) với \(p\) là nửa chu vi tam giác \(ABM\).
Giải thích thêm:
Cách 2:
Kẻ MN vuông góc với AC => N là trung điểm AC
$\Rightarrow MNBB'$ là hình chữ nhật
$\Rightarrow$ $B'N$ cắt $MB$ tại trung điểm của $B'N$
$\Rightarrow d\left(B^{\prime},(A B M)\right)=d(N,(A B M))$
Kẻ $\mathrm{NP}$ vuông góc $\mathrm{AB}$
Ta có: $NP=\dfrac{NB}{2}=2 $
$\Rightarrow d(N,(A M B))=\sqrt{\dfrac{1}{\dfrac{1}{NM^{2}}+\dfrac{1}{NP^{2}}}}=4 \Rightarrow d\left(B^{\prime},(A B M)\right)=4$


