Đề thi tư duy định lượng - Đề số 4

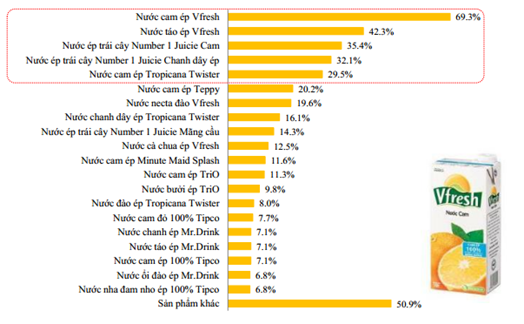
Các loại nước của nhãn hiệu Vfresh chiếm tỉ lệ người dùng cao nhất đặc biệt là sản phẩm nước cam ép chiếm bao nhiêu phần trăm?

Để hai đồ thị $y = - {x^2} - 2x + 3$ và $y = {x^2} - m$ có hai điểm chung thì:

Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(2a\), tam giác \(SAB\) cân tại \(S\) và nằm trong mặt phẳng vuông góc với đáy. Góc giữa hai mặt phẳng \(\left( {SCD} \right)\) và \(\left( {ABCD} \right)\) bằng \(\varphi \) và \(\sin \varphi  = \dfrac{{\sqrt 5 }}{5}\). Khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {SCD} \right)\) là \(\dfrac{{2\sqrt 5 a}}{k}\)

Tìm $k$.

Hệ phương trình \(\left\{ \begin{array}{l}{x^2} = 3x - y\\{y^2} = 3y - x\end{array} \right.\) có bao nhiêu nghiệm?

Tập nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}2x - 1 \ge 0\\4 - 3x \ge 0\end{array} \right.\) là

Trong mặt phẳng với hệ tọa độ $Oxy,$ cho $\Delta ABC$ cân có đáy là $BC.$  Đỉnh $A$  có tọa độ là các số dương, hai điểm $B$  và $C$  nằm trên trục $Ox,$  phương trình cạnh $AB:$ $y = 3\sqrt 7 (x - 1)$. Biết chu vi của $\Delta ABC$ bằng $18,$  tìm tọa độ các đỉnh $A,B,C.$

Với điều kiện nào của \(m\)  thì phương trình sau đây là phương trình đường tròn \({x^2} + {y^2} - 2(m + 2)x + 4my + 19m - 6 = 0\) ?

Phương trình \(\sqrt 3 \sin 2x - \cos 2x + 1 = 0\) có nghiệm là:

Độ dài $3$ cạnh của một tam giác vuông lập thành một cấp số cộng . Nếu trung bình cộng ba cạnh bằng $6$ thì công sai của cấp số cộng này là:

Một thầy giáo có 20 quyển sách khác nhau gồm 7 quyển sách Toán, 5 quyển sách Lí và 8 quyển sách Hóa. Thầy chọn ra 9 quyển sách để tặng cho học sinh. Hỏi thầy giáo đó có bao nhiêu cách chọn sao cho số sách còn lại của thầy có đủ 3 môn?

Gọi \(S\) là tập hợp tất cả các số tự nhiên có 4 chữ số phân biệt. Chọn ngẫu nhiên 1 số từ \(S\). Xác suất chọn được số lớn hơn \(2500\) là

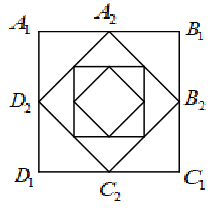
Cho hình vuông $A_{1} B_{1} C_{1} D_{1}$ có cạnh bằng a và có diện tích $S_{1}$. Nối bốn trung điểm $A_{2}, B_{2}, C_{2}, D_{2}$ ta được hình vuông thứ hai có diện tích $S_{2}$. Tiếp tục như thế, ta được hình vuông $A_{3} B_{3} C_{3} D_{3}$ có diện tích $S_{3}, \ldots$ Tính tổng $S_{1}+S_{2}+\ldots$ bằng

Cho hàm số \(y = \dfrac{1}{3}{x^3} - \dfrac{m}{2}{x^2} + mx + 5\). Tìm tất cả các giá trị của tham số m để \(y' \ge 0,\forall x \in \mathbb{R}\).

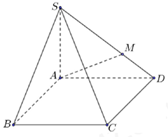
Cho hình chóp \(S.ABC{\rm{D}}\) có đáy \(ABC{\rm{D}}\) là hình bình hành. Gọi điểm \(M\) là điểm thuộc cạnh \(S{\rm{D}}\) sao cho \(SM = \dfrac{2}{3}SD\) (minh họa như hình vẽ). Mặt phẳng chứa \(AM\) và song song với \(B{\rm{D}}\) cắt cạnh \(SC\) tại \(K\). Tỷ số \(\dfrac{{SK}}{{SC}}\) bằng

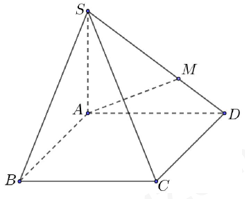
Cho lăng trụ đều \(ABC.A'B'C'\) có tất cả các cạnh bằng a. Gọi \(\alpha \) là góc giữa mặt phẳng \(\left( {A'BC} \right)\) và mặt phẳng \(\left( {ABC} \right)\). Biết \(\tan \alpha = \dfrac{{k\sqrt 3 }}{3}\). Tìm số nguyên $k$.

Nếu \(\int\limits_1^2 {\dfrac{{dx}}{{x + 3}}} \) được viết dưới dạng \(\ln \dfrac{a}{b}\) với \(a,b\) là các số tự nhiên và ước chung lớn nhất của \(a,b\) là \(1\). Chọn khẳng định sai:

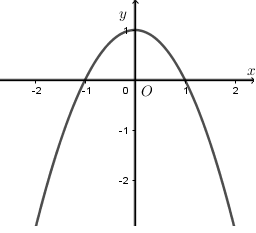
Gọi $S$ là diện tích của Ban Công của một ngôi nhà có dạng như hình vẽ ($S$ được giới hạn bởi parabol $\left( P \right)$  và trục $Ox$). Giá trị của S là:

Cho \(\int_0^{\frac{\pi }{{18}}} f (\sin (3x))\cos (3x)dx = 3\) và \(\int_{\frac{1}{2}}^2 f (1 - x)dx = 4\). Tính \(I = \int_{ - 1}^0 f (x)d\)

Cho tích phân $I = \int\limits_1^2 {\dfrac{{x + \ln x}}{{{{\left( {x + 1} \right)}^3}}}{\rm{d}}x}  = a + b.\ln 2 - c.\ln 3$ với $a,b,c \in R$, tỉ số $\dfrac{c}{a}$ bằng

Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi các đường \(y = {x^2} + 1;x = 0\) và tiếp tuyến của đồ thị hàm số \(y = {x^2} + 1\) tại điểm \(A\left( {1;2} \right)\) quanh trục $Ox$ là

Một người vay ngân hàng một số tiền với lãi suất mỗi tháng là $1,12\% $. Biết cuối mỗi tháng người đó phải trả cho ngân hàng $3.000.000$ đồng và trả trong $1$ năm thì hết nợ. Số tiền người đó vay là:

Tập nghiệm của bất phương trình \({3^{\sqrt {2x}  + 1}} - {3^{x + 1}} \le {x^2} - 2x\) là:

Phương trình ${\log _2}\left( {x - 3} \right) + 2{\log _4}3.{\log _3}x = 2$ có tất cả bao nhiêu nghiệm?

Tìm tất cả các giá trị của tham số \(m\) để hàm số \(y =  - {x^3} - 3{x^2} + mx + 2\) có cực đại và cực tiểu?

Tìm giá trị của m để hàm số \(y =  - {x^2} + 2x + m - 5\) đạt giá trị lớn nhất bằng 6.

Cho hình chóp S.ABCD có ABCD là hình chữ nhật, \(AB = 2a,\)\(AD = a\)\(\left( {a > 0} \right)\). M là trung điểm của AB, tam giác SMC vuông tại S, \(\left( {SMC} \right) \bot \left( {ABCD} \right),\)\(SM\) tạo với đáy góc \(60^\circ \). Thể tích của khối chóp S.ABCD là:

Cho số phức $z = 2 + 3i$. Tìm số phức \(w = \left( {3 + 2i} \right)z + 2\overline z \)

Biết rằng \(z\) là số phức có môđun nhỏ nhất thỏa mãn \(\left( {1 - z} \right)\left( {\bar z + 2i} \right)\) là số thực. Số phức \(z\) là:

Với số phức \(z\) thỏa mãn \(\left| {z - 2 + i} \right| = 4\), tập hợp các điểm biểu diễn các số phức \(z\) là một đường tròn. Tìm bán kính \(R\) của đường tròn đó.

Cho số phức $z$ thỏa mãn $\left( {1 + i} \right)z = 3-i$. Hỏi điểm biểu diễn của $z$ là điểm nào trong các điểm $M,N,P,Q$ ở hình bên ?

Trong không gian với hệ toạ độ $Oxyz$, cho hai mặt phẳng  $\left( P \right):x + 2y + 2z + 11 = 0$  và  $\left( Q \right):x + 2y + 2z + 2 = 0$ . Tính khoảng cách giữa $\left( P \right)$ và $\left( Q \right)$.

Trong không gian $Oxyz$, cho ba mặt phẳng $(P): x+y+z-1=0$, $(Q): 2 x+m y+2 z+3=0$ và $(R):-x+2 y+n z=0$. Tính tổng $m+2 n$, biết $(P) \perp(R)$ và $(P) / /(Q)$

Trong không gian \(Oxyz\) cho hai điểm \(A\left( {0; - 2;3} \right),B\left( {1;0; - 1} \right)\). Tính sin góc hợp bởi hai véc tơ \(\overrightarrow {OA} ,\overrightarrow {OB} \).

Trong không gian với hệ tọa độ Oxyz cho điểm \(A( - 2;2; - 2)\) và điểm \(B(3; - 3;3)\). Điểm \(M\) thay đổi trong không gian thỏa mãn \(\dfrac{{MA}}{{MB}} = \dfrac{2}{3}\). Điểm \(N(a;b;c)\) thuộc mặt phẳng \((P): - x + 2y - 2z + 6 = 0\) sao cho MN nhỏ nhất. Tính tổng \(T = a + b + c\).

Trong một mạch điện kín nếu mạch ngoài thuần điện trở R_N thì hiệu suất của nguồn điện có điện trở r được tính bởi biểu thức:

Trong không gian \(Oxyz\), cho đường thẳng  \(d:\dfrac{x}{{ - 2}} = \dfrac{{y - 1}}{1} = \dfrac{z}{1}\) và mặt phẳng \(\left( P \right):2x - y + 2z - 2 = 0.\) Có bao nhiêu điểm \(M\) thuộc d  sao cho M cách đều gốc tọa độ O và mặt phẳng \(\left( P \right)\)?

Trong không gian \(Oxyz,\) cho điểm \(M\left( {1;\,\,6; - 3} \right)\) và mặt phẳng \(\left( P \right):\,\,\,2x - 2y + z - 2 = 0.\)  Khoảng cách từ \(M\) đến \(\left( P \right)\) bằng:

Trong không gian Oxyz, cho hai đường thẳng chéo nhau \({d_1}:\dfrac{{x - 2}}{2} = \) \(\dfrac{{y - 6}}{{ - 2}} = \dfrac{{z + 2}}{1}\) và \({d_2}:\dfrac{{x - 4}}{1} = \dfrac{{y + 1}}{3} = \dfrac{{z + 2}}{{ - 2}}\). Phương trình mặt phẳng \((P)\) chứa \({d_1}\) và \((P)\) song song với đường thẳng \({d_2}\) là

Cho tam giác \(ABC\) có tọa độ \(3\) đỉnh \(A\left( {1;2;3} \right),B\left( {0; - 1;1} \right)\) và \(C\left( { - 1;1;1} \right)\). Diện tích tam giác là:

Cho một cái bể nước hình hộp chữ nhật có ba kích thước $2m,3m,2m$ lần lượt là chiều dài, chiều rộng, chiều cao của lòng trong đựng nước của bể. Hàng ngày nước ở trong bể được lấy ra bởi một cái gáo nước hình trụ có chiều cao là $5cm$ và bán kính đường tròn đáy là $4cm$. Trung bình một ngày được múc ra $170$ gáo nước để sử dụng (Biết mỗi lần múc là múc đầy gáo). Hỏi sau bao nhiêu ngày thì bể hết nước biết rằng ban đầu bể đầy nước?

Cho lăng trụ đứng \(ABC.A'B'C'\) với $ABC$ là tam giác vuông cân tại $C$ có \(AB = a\) , mặt bên \(ABB'A'\) là hình vuông. Mặt phẳng qua trung điểm $I$ của $AB$ và vuông góc với \(AB'\) chia khối lăng trụ thành 2 phần. Tính thể tích mỗi phần?

Cho hàm số \(y =  - {x^3} + \left( {2m - 1} \right){x^2} - \left( {{m^2} - 1} \right)x + 2019\). Hỏi có bao nhiêu giá trị nguyên của tham số \(m\) thuộc khoảng \(\left( { - 2019;2019} \right)\) để hàm số nghịch biến trên khoảng \(\left( {2; + \infty } \right)\)?

Số điểm cực trị của hàm số \(y = \left| {{x^2} - 3x + 2} \right|\) là:

Hàm số \(y = \left( {{x^2} - 1} \right){\left( {3x - 2} \right)^3}\) có bao nhiêu điểm cực đại?

Hàm số \(f\left( x \right) = \left| {\dfrac{x}{{{x^2} + 1}} - m} \right|\) (với \(m\) là tham số thực) có nhiều nhất bao nhiêu điểm cực trị?

Cho hình tứ diện đều \(ABCD\) có độ dài các cạnh bằng \(1\). Gọi \(A',\,\,B',\,\,C',\,\,D'\) lần lượt là điểm đối xứng của \(A,\,\,B,\,\,C,\,\,D\) qua các mặt phẳng \(\left( {BCD} \right),\,\,\left( {ACD} \right),\,\,\left( {ABD} \right),\,\,\left( {ABC} \right)\). Tính thể tích của khối tứ diện \(A'B'C'D'\).

Cho hàm số $y = f\left( x \right) = \dfrac{{{x^3}}}{3} - m{x^2} - 6mx - 9m + 12$ có đồ thị hàm số $\left( {{C_m}} \right)$. Khi tham số m thay đổi, các đồ thị $\left( {{C_m}} \right)$ đều tiếp xúc với một đường thẳng cố định. Đường thẳng này có phương trình:

Xét các số thực dương \(a\) và \(b\) thỏa mãn \({\log _3}\left( {1 + ab} \right) = \dfrac{1}{2} + {\log _3}\left( {b - a} \right)\). Giá trị nhỏ nhất của biểu thức \(P = \dfrac{{\left( {1 + {a^2}} \right)\left( {1 + {b^2}} \right)}}{{a\left( {a + b} \right)}}\) bằng:

Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) có bảng biến thiên như hình vẽ:

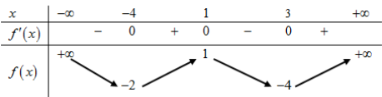
Số nghiệm của phương trình \(\left| {f\left( {f\left( x \right)} \right)} \right| = 2\) là:

Gọi \(M,\,\,N\) lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(f\left( x \right) = \left| {x - 3} \right|\sqrt {x + 1} \) trên đoạn \(\left[ {0;4} \right]\). Tính\(M + 2N\).