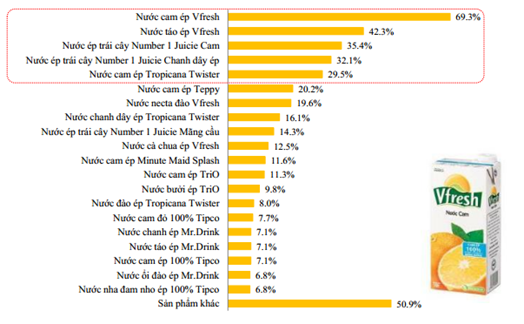
Trả lời bởi giáo viên
Xét hàm số \(y = {x^2} - 3x + 2\) ta có: \(y' = 2x - 3 \Rightarrow y' = 0\) \( \Leftrightarrow 2x - 3 = 0\) \( \Leftrightarrow x = \dfrac{3}{2}\)
\( \Rightarrow \) Hàm số \(y = {x^2} - 3x + 2\) có 1 cực trị.
Xét phương trình hoành độ giao điểm của đồ thị hàm số \(y = {x^2} - 3x + 2\) với trục hoành ta có:
\({x^2} - 3x + 2 = 0\) \( \Leftrightarrow \left( {x - 1} \right)\left( {x - 2} \right) = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 2\end{array} \right.\)
\( \Rightarrow \) Đồ thị hàm số \(y = {x^2} - 3x + 2\) cắt trục hoành tại 2 điểm phân biệt.
\( \Rightarrow \) Số điểm cực trị của hàm số \(y = \left| {{x^2} - 3x + 2} \right|\) là: \(S = 1 + 2 = 3\) cực trị.
Hướng dẫn giải:
Số điểm cực trị của hàm số \(y = \left| {f\left( x \right)} \right|\) là \(S = a + b\) với \(a\) là số cực trị của hàm số \(y = f\left( x \right)\) và \(b\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) với trục \(Ox.\)
Giải thích thêm:
Có thể vẽ đồ thị hàm số và suy ra kết luận, chẳng hạn:
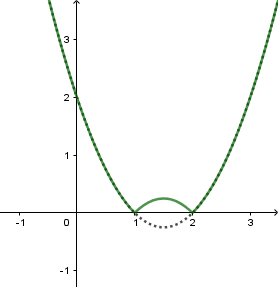
Từ đồ thị suy ra hàm số đã cho có 3 điểm cực trị.