Đề thi tư duy định lượng - Đề số 3

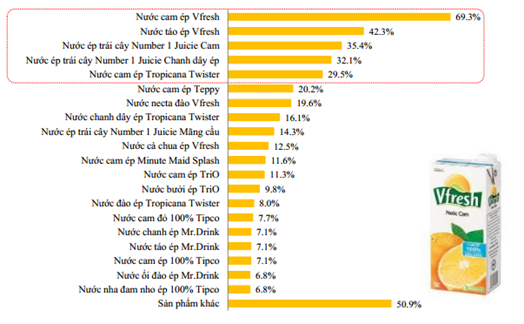
Dòng sản phẩm nào có tỷ lệ người dùng ở vị trí thứ hai là:

Số nghiệm của phương trình$\sqrt {{{\rm{x}}^4} - 2{{\rm{x}}^2} + 1}  = 1 - x$ là:

Cho tứ diện $OABC$ có ba cạnh $OA,\,\,OB,\,\,OC$ đôi một vuông góc với nhau. Biết khoảng cách từ điểm $O$ đến các đường thẳng $BC,\,\,CA,\,\,AB$ lần lượt là $a,\,\,a\sqrt 2 ,\,\,a\sqrt 3$. Khoảng cách từ điểm $O$ đến mặt phẳng $\left( {ABC} \right)$ là $\dfrac{{2a\sqrt {m} }}{{11}}$. Tìm $m$.

Tìm nghiệm của hệ phương trình: $\left\{ \begin{array}{l}x\sqrt 2  - y\sqrt 3  = 1\\x\sqrt 3  + y\sqrt 2  = 5\end{array} \right.$.

Trong mặt phẳng với hệ toạ độ $Oxy,$  cho $4$ điểm $A\left( {1;0} \right),B\left( {-2;4} \right),C\left( {-1;4} \right),D\left( {3;5} \right).$ Tìm toạ độ điểm $M$  thuộc đường thẳng $(\Delta ):3x - y - 5 = 0$ sao cho hai tam giác $MAB,MCD$  có diện tích bằng nhau.

Tìm tọa độ tâm $I$ của đường tròn đi qua ba điểm $A\left( {0;4} \right)$, $B\left( {2;4} \right)$, $C\left( {4;0} \right)$.

Phương trình $\cot 20x = 1$ có bao nhiêu nghiệm thuộc khoảng $\left[ { - 50\pi ;0} \right]$?

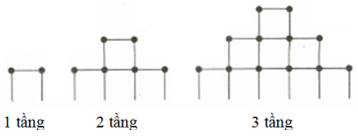
Bạn An chơi trò chơi xếp các que diêm thành tháp theo qui tắc thể hiện như hình vẽ. Để xếp được tháp có $10$ tầng thì bạn An cần đúng bao nhiêu que diêm?

Từ các chữ số 0; 1; 2; 3; 5; 8 có thể lập được bao nhiêu số tự nhiên lẻ có bốn chữ số đôi một khác nhau và phải có mặt chữ số 3.

Từ một hộp chứa $6$ quả cầu trắng và $4$ quả cầu đen, lấy ra ngẫu nhiên cùng một lúc $4$ quả. Xác suất để lấy ra được ít nhất một quả màu đen là:

Người ta dự định xây dựng một tòa tháp 11 tầng tại một ngôi chùa nọ theo cấu trúc: diện tích của mặt sàn tầng trên bằng một nửa diện tích mặt sàn tầng dưới, biết diện tích mặt đáy tháp là $15 \mathrm{~m}^{2}$. Yêu cầu là nền tháp lát gạch hoa kích thước $30 \mathrm{x} 30$ $(\mathrm{cm})$. Số lượng gạch hoa cần mua để lát sàn tháp là

Cho hàm số $y = \sqrt {10x - {x^2}}$. Giá trị của $y'\left( 2 \right)$ bằng

Cho tứ diện đều $SABC.$ Gọi $I$ là trung điểm của $AB, M$ là một điểm di động trên đoạn $AI.$ Gọi $(P)$ là mặt phẳng qua $M$ và song song với $SI, IC,$ biết $AM = x.$ Thiết diện tạo bởi $mp(P)$ và tứ diện $SABC$ có chu vi là:

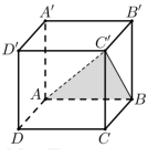
Cho hình lăng trụ tứ giác đều $ABCD.A'B'C'D'$ có cạnh đáy bằng $a$, cạnh bên bằng $a\sqrt 3$. Tính cosin của góc giữa hai mặt phẳng $\left( {ABCD} \right)$ và $\left( {ABC'} \right)$?

Tìm họ nguyên hàm của hàm số $f\left( x \right) = \dfrac{{{x^2} - 2x + 1}}{{x - 2}}$

Một xe ô tô đang chuyển động đều với vận tốc 16 m/s thì người lái xe nhìn thấy một chướng ngại vật nên đạp phanh. Từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc $v\left( t \right) =  - 2t + 16$ trong đó t là thời gian (tính bằng giây) kể từ lúc đạp phanh. Quãng đường mà ô tô đi được trong 10 giây cuối cùng bằng:

Biết hàm số $y = f\left( x \right)$ liên tục và có đạo hàm trên $\left[ {0;\,\,2} \right],$$f\left( 0 \right) = \sqrt 5 ,$$f\left( 2 \right) = \sqrt {11} .$ Tích phân $I = \int\limits_0^2 {f\left( x \right).f'\left( x \right)dx}$ bằng:

Cho $f\left( x \right)$ là một hàm số có đạo hàm liên tục trên $\mathbb{R}$ và thỏa mãn $f\left( 1 \right) = 1$ và $\int\limits_0^1 {f\left( t \right){\rm{dt}}}  = \dfrac{1}{3}.$ Giá trị của tích phân $I = \int\limits_0^{\frac{\pi }{2}} {\sin 2x.f'\left( {\sin x} \right){\rm{d}}x}$ bằng:

Cho hình phẳng $\left( H \right)$ giới hạn bởi các đường $y =  - \,{x^2} + 2x$ và $y = 0$. Tính thể tích của khối tròn xoay tạo thành khi quay hình $\left( H \right)$ quanh trục $Oy$ là

Anh A mua 1 chiếc Laptop giá $23$ triệu đồng theo hình thức trả góp, lãi suất mỗi tháng là $0,5\%$. Hỏi mỗi tháng anh A phải trả cho cửa hàng bao nhiêu tiền để sau $6$ tháng anh trả hết nợ?

Tập hợp nghiệm của bất phương trình: ${3^{3x - 2}} + \dfrac{1}{{{{27}^x}}} \le \dfrac{2}{3}$ là:

Tính tổng $T$ tất cả các nghiệm của phương trình ${4.9^x} - {13.6^x} + {9.4^x} = 0$.

Với tất cả giá trị nào của $m$ thì hàm số $y = m{x^4} + \left( {m - 1} \right){x^2} + 1 - 2m$ chỉ có một cực trị

Giá trị lớn nhất của hàm số $y =  - {x^2} + 4x - 1$ là:

Cho hình chóp $S.ABC$, đáy là tam giác $ABC$ có $AB = BC\sqrt 5$, $AC = 2BC\sqrt 2$, hình chiếu của $S$ lên mặt phẳng $\left( {ABC} \right)$ là trung điểm $O$ của cạnh $AC$. Khoảng cách từ $A$ đến mặt phẳng $\left( {SBC} \right)$ bằng 2. Mặt phẳng $\left( {SBC} \right)$ hợp với mặt phẳng $\left( {ABC} \right)$ một góc $\alpha$ thay đổi. Biết rằng giá trị nhỏ nhất của thể tích khối chóp $S.ABC$ bằng $\dfrac{{\sqrt a }}{b}$, trong đó $a,\,\,b \in {\mathbb{N}^*}$, $a$ là số nguyên tố. Tổng $a + b$ bằng:

Tìm các số thực $x,\,\,y$ thỏa mãn đẳng thức $3x + y + 5xi = 2y - \left( {x - y} \right)i$.

Cho số phức $z$ thay đổi, luôn có $\left| z \right| = 2$ . Khi đó tập hợp điểm biểu diễn số phức ${\rm{w}} = (1 - 2i)\overline z  + 3i$ là

Trong mặt phẳng phức, tập hợp các điểm biểu diễn các số phức z thỏa mãn $z.\bar z = 1$ là đường tròn có bán kính là:

Cho các số phức ${z_1} = 2,{z_2} =  - 4i,{z_3} = 2 - 4i$ có điểm biểu diễn tương ứng trên mặt phẳng tọa độ Oxy là A, B, C. Diện tích tam giác ABC bằng

Trong không gian với hệ tọa độ $Oxyz$, cho hai mặt phẳng $\left( P \right):mx + y - 2z - 2 = 0$  và $\left( Q \right):x - 3y + mz + 5 = 0$. Tìm tất cả các giá trị thực của $m$ để hai mặt phẳng đã cho vuông góc với nhau.

Đề thi THPT QG – 2021 lần 1– mã 104

Trong không gian $Oxyz,$ cho hai điểm $A\left( {1;0;0} \right)$ và $B\left( {3;2;1} \right).$ Mặt phẳng đi qua $A$ và vuông góc với $AB$ có phương trình là:

Trong không gian với hệ tọa độ $Oxyz$ cho điểm $A\left( 1;-4;-5 \right)$ Tọa độ điểm $A'$ đối xứng với điểm $A$ qua mặt phẳng $\left( Oxz \right)$ là:

Trong không gian với hệ tọa độ $Oxyz$, cho hai đường thẳng $d:\left\{ \begin{array}{l}x = 2t\\y = t\\z = 4\end{array} \right.$ và $d':\left\{ \begin{array}{l}x = t'\\y = 3 - t'\\z = 0\end{array} \right.$ . Phương trình mặt cầu có đường kính là đoạn thẳng vuông góc chung của hai đường thẳng $d$ và $d'$ là: 

Trong không gian với hệ trục tọa độ ${\mathop{\rm Oxyz}\nolimits}$, cho điểm $A(4; - 3;5)$ và $B(2; - 5;1).$Viết phương trình mặt phẳng $(P)$ đi qua trung điểm $I$ của đoạn thẳng $AB$ và vuông góc với đường thẳng $(d):\dfrac{{x + 1}}{3} = \dfrac{{y - 5}}{{ - 2}} = \dfrac{{z + 9}}{{13}}$.

Trong không gian với hệ tọa độ  $Oxyz$, cho hai điểm  $A(0;2; - 1)$ , $B(2;0;1)$. Tìm tọa độ điểm $M$ thuộc trong mặt phẳng $\left( {Oyz} \right)$ sao cho :$M{A^2} + M{B^2}$ đạt giá trị bé nhất.

Trong không gian với hệ trục $Oxyz$, khoảng cách từ điểm $M\left( { - 2;3;4} \right)$ đến mặt phẳng $\left( P \right):2x - 2y + z + 3 = 0$ bằng:

Trong không gian $Oxyz$, cho đường thẳng  $d:\dfrac{x}{{ - 2}} = \dfrac{{y - 1}}{1} = \dfrac{z}{1}$ và mặt phẳng $\left( P \right):2x - y + 2z - 2 = 0.$ Có bao nhiêu điểm $M$ thuộc d  sao cho M cách đều gốc tọa độ O và mặt phẳng $\left( P \right)$?

Trong không gian với hệ tọa độ $Oxyz$, cho ba điểm$A(1;1;1),B( - 1; - 1;0)$ và $C(3;1; - 1)$. Tìm tọa độ điểm $M$ thuộc $\left( {Oxy} \right)$  và cách đều các điểm $A,B,C$ .

Một đội xây dựng cần hoàn thiện một hệ thống cột tròn của một cửa hàng kinh doanh gồm $17$ chiếc. Trước khi hoàn thiện mỗi chiếc cột là một khối bê tông cốt thép hình lăng trụ lục giác đều có cạnh $14cm$; sau khi hoàn thiện (bằng cách trát thêm vữa tổng hợp vào xung quanh) mỗi cột là một khối trụ có đường kính đáy bằng$30cm$. Biết chiều cao của mỗi cột trước và sau khi hoàn thiện là $390cm$. Tỉnh lượng vữa hỗn hợp cần dùng (tính theo đơn vị ${m^3}$, làm tròn đến $1$ chữ số thập phân sau dấu phầy). Ta có kết quả:

Cho hình chóp đều $S.ABCD$ có diện tích đáy là $16c{m^2}$, diện tích một mặt bên là $8\sqrt 3 c{m^2}$. Thể tích khối chóp $S.ABCD$ là:

Xác định giá trị của tham số $m$ để hàm số  $y = {x^3} - 3m{x^2} - m$ nghịch biến trên khoảng $\left( {0;1} \right)$.

Cho hàm số bậc bốn $y = f\left( x \right)$ có đồ thị như hình dưới đây:

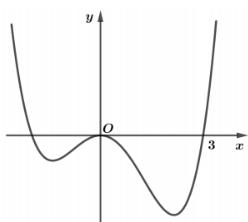
Số điểm cực trị của hàm số $g\left( x \right) = f\left( {{x^3} - 3{x^2}} \right)$ là:

Cho hàm số $y = f\left( x \right)$ có đạo hàm $f'\left( x \right) = {x^2}\left( {{x^2} - 1} \right)$. Điểm cực tiểu của hàm số $y = f\left( x \right)$ là:

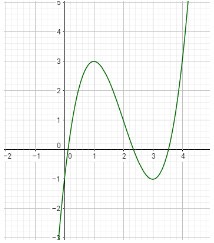
Cho đồ thị (C) của hàm số $y = {x^3} - 6{x^2} + 9x - 1$ như hình vẽ. Hãy xác định số điểm cực trị của hàm số $y = {\left| x \right|^3} - 6{x^2} + 9\left| x \right| - 1$.

Cho hình chóp tam giác đều $S.ABC$ có cạnh đáy bằng $a$ và mặt bên hợp với đáy một góc ${60^0}$. Thể tích khối chóp $S.ABC$ là:

Cho hàm số $y = \dfrac{{2x - 2}}{{x - 2}}$ có đồ thị là$\left( C \right)$, $M$là điểm thuộc $\left( C \right)$ sao cho tiếp tuyến của $\left( C \right)$ tại $M$cắt hai đường tiệm cận của $\left( C \right)$ tại hai điểm $A$, $B$ thỏa mãn $AB = 2\sqrt 5$. Gọi $S$ là tổng các hoành độ của tất cả các điểm $M$thỏa mãn bài toán. Tìm giá trị của $S$.

Có tất cả bao nhiêu giá trị nguyên của $y$ sao cho tương ứng với mọi $y$ luôn tồn tại không quá 63 số nguyên $x$ thỏa mãn điều kiện ${\log _{2020}}\left( {x + {y^2}} \right) + {\log _{2021}}\left( {{y^2} + y + 64} \right) \ge {\log _4}\left( {x - y} \right).$

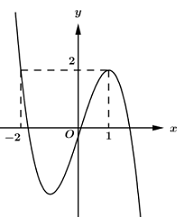
Cho hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$ và có đồ thị như hình vẽ bên. Số nghiệm của phương trình $f\left( {1 - f\left( x \right)} \right) = 2$ là:

Đề thi THPT QG – 2021 lần 1– mã 104

Trên đoạn $\left[ { - 1;2} \right],$ hàm số $y = {x^3} + 3{x^2} + 1$ đạt giá trị nhỏ nhất tại điểm