Đề thi tư duy định lượng - Đề số 10

Dựa vào các thông tin được cung cấp dưới đây để trả lời câu hỏi sau:

Ngày 29 tháng 2, giá xăng RON 95-III nhiều hơn giá xăng ES RON 92 bao nhiêu phần trăm?

Tìm giá trị của m để đồ thị hàm số $y = {x^2} - 2x + m - 1$ cắt trục hoành tại hai điểm phân biệt có hoành độ dương.

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, $BC = a$. Cạnh bên $SA$ vuông góc với đáy, góc $\widehat {SCA} = \widehat {BSC} = {30^0}$. Gọi $M$ là trung điểm của $CD$. Tính khoảng cách từ $D$ đến mặt phẳng $\left( {SAM} \right)$.

Các nghiệm của hệ $\left\{ \begin{array}{l}xy - 3x - 2y = 16\\{x^2} + {y^2} - 2x - 4y = 33\end{array} \right.$ là

Cho biểu thức \(f\left( x \right) = 9{x^2} - 1.\) Tập hợp tất cả các giá trị của \(x\) để \(f\left( x \right) < 0\) là

Cho hai điểm \(A(6;2)\)  và \(B( - 2;0).\) Phương trình đường tròn $(C)$ có đường kính $AB$ là:

Phương trình \(\sin 2x + 3\sin 4x = 0\) có nghiệm là:

Một người làm việc cho một công ty. Theo hợp đồng trong năm đầu tiên, tháng lương thứ nhất là 6 triệu đồng và lương tháng sau cao hơn tháng trước là 200 ngàn đồng. Hỏi theo hợp đồng tháng thứ 7 người đó nhận được lương là bao nhiêu?

Lớp 11A có 15 học sinh nữ, 20 học sinh nam. Có bao nhiêu cách chọn 5 học sinh tham gia văn nghệ trong đó có ít nhất 3 học sinh nữ?

Một người chơi trò gieo súc sắc. Mỗi ván gieo đồng thời ba con súc sắc. Người chơi thắng cuộc nếu xuất hiện ít nhất 2 mặt sáu chấm. Tính xác suất để trong ba ván, người đó thắng ít nhất hai ván

Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và \(\mathop {\lim }\limits_{x \to 2} \dfrac{{f\left( x \right) - 1}}{{{x^2} - x - 2}} = 3\). Tính \(\mathop {\lim }\limits_{x \to 2} \dfrac{{{f^3}\left( x \right) + 3f\left( x \right) - 4}}{{{x^2} - 2x}}\)

Cho hàm số \(y = \sqrt {10x - {x^2}} \). Giá trị của \(y'\left( 2 \right)\) bằng

Cho hình hộp \(ABCD.A'B'C'D'\). Trên các cạnh \(AA'\), \(BB'\), \(CC'\) lần lượt lấy ba điểm \(M\), \(N\), \(P\) sao cho \(\dfrac{{A'M}}{{AA'}} = \dfrac{1}{3}\), \(\dfrac{{B'N}}{{BB'}} = \dfrac{2}{3}\), \(\dfrac{{C'P}}{{CC'}} = \dfrac{1}{2}\). Biết mặt phẳng \(\left( {MNP} \right)\) cắt cạnh \(DD'\) tại \(Q\). Tính tỉ số \(\dfrac{{D'Q}}{{DD'}}\).

Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a\) và \(SA = SB = SC = b\). Gọi G là trọng tâm \(\Delta ABC\). Xét mặt phẳng \((P)\) đi qua \(A\) và vuông góc với \(SC\). Tìm hệ thức liên hệ giữa \(a\) và \(b\) để \((P)\) cắt \(SC\) tại điểm \({C_1}\) nằm giữa \(S\) và \(C\).

Cho hàm số \(y = f\left( x \right)\) thỏa mãn \(f\left( 2 \right) =  - \dfrac{4}{{19}}\) và \(f'\left( x \right) = {x^3}{f^2}\left( x \right)\,\,\forall x \in \mathbb{R}\). Giá trị của \(f\left( 1 \right)\) bằng:

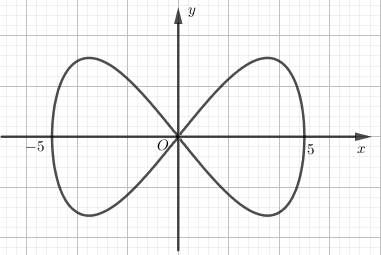
Trong Công viên Toán học có những mảnh đất hình dáng khác nhau. Mỗi mảnh được trồng một loài hoa và nó được tạo thành bởi một trong những đường cong đẹp nhất trong toán học. Ở đó có mảnh đất mang tên Bernoulli, nó được tạo thành từ đường Lemniscate có phương trình trong hệ tọa độ $Oxy$ là \(16{y^2} = {x^2}\left( {25 - {x^2}} \right)\) như hình vẽ bên. Tính diện tích $S$ của mảnh đất Bernoulli biết rằng mỗi đơn vị trong hệ trục tọa độ $Oxy$ tương ứng với chiều dài $1$ mét

Cho \(\int\limits_0^1 {f\left( x \right)dx = 1.} \) Tính \(\int\limits_0^{\frac{\pi }{4}} {\left( {2{{\sin }^2}x - 1} \right)f\left( {\sin 2x} \right)dx.} \)

Tính tích phân \(I = \int\limits_1^{{2^{1000}}} {\dfrac{{\ln x}}{{{{(x + 1)}^2}}}dx} \)

Cho hình phẳng \((D)\) được giới hạn bởi các đường \(x = 0,\,\,x = \pi ,\,\,y = 0\) và \(y=-\sin x.\) Thể tích \(V\) của khối tròn xoay tạo thành khi quay \((D)\) xung quanh trục \(Ox\) được tính theo công thức

Bạn An gửi vào ngân hàng số tiền là $2.000.000$ đồng với kì hạn $3$ tháng và lãi suất là $0,48\% $ mỗi tháng. Tính số tiền An có được sau $3$ năm.

Nghiệm của bất phương trình \({e^x} + {e^{ - x}} < \dfrac{5}{2}\) là

Cho các số dương \(x,\,\,y\) thỏa mãn \({2^{{x^3} - y + 1}} = \dfrac{{2x + y}}{{2{x^3} + 4x + 4}}\). Giá trị nhỏ nhất của biểu thức \(P = \dfrac{7}{y} + \dfrac{{{x^3}}}{7}\) có dạng $\dfrac{a}{b}$. Tính $a-b$.

Đề thi THPT QG - 2021 - mã 103

Nghiệm của phương trình \({\log _3}\left( {2x} \right) = 2\) là:

Cho hàm số $y = {x^4} - 2m{x^2} + 3m + 2.$ Tất cả các giá trị của $m$ để đồ thị hàm số có $3$ điểm cực trị tạo thành tam giác đều là:

Parabol \(\left( P \right):y = a{x^2} + bx + c\) có đồ thị như hình dưới. Tính \(M = 4a + 2b - 3c?\)

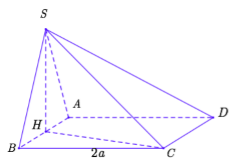
Cho tứ diện \(ABCD\) có \(AB = a\sqrt 6 ,\) tam giác \(ACD\) đều, hình chiếu vuông góc của \(A\) lên mặt phẳng \(\left( {BCD} \right)\) trùng với trực tâm \(H\) của tam giác \(BCD,\) mặt phẳng \(\left( {ADH} \right)\) tạo với mặt phẳng \(\left( {ACD} \right)\) một góc \({45^0}.\) Tính thể tích khối tứ diện \(ABCD.\)

Cho số phức \(z =  - \dfrac{1}{2} + \dfrac{{\sqrt 3 }}{2}i\). Số phức \(1 + z + {z^2}\) bằng:

Tìm tập hợp các điểm trên mặt phẳng tọa độ biểu diễn các số phức \(z\) thỏa mãn điều kiện \(|z(i + 1) - 1 - i| = \sqrt 2 \).

Gọi \({z_1}\) là nghiệm phức có phần ảo âm của phương trình \({z^2} - 2z + 5 = 0\). Hỏi điểm biểu diễn của \(w = (1 + i){z_1}\) là điểm nào trong các điểm trong các điểm M, N, P, Q ở hình bên?

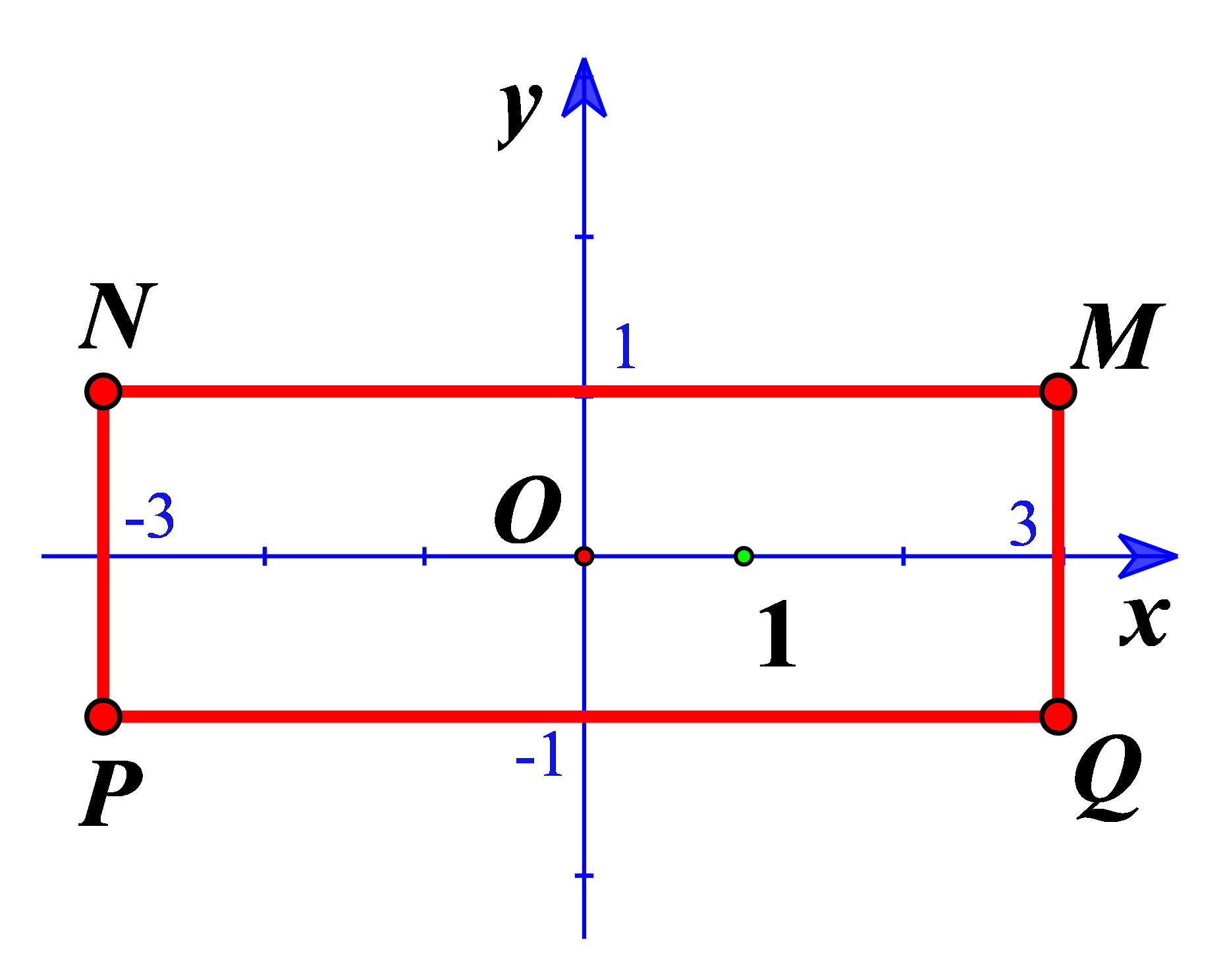
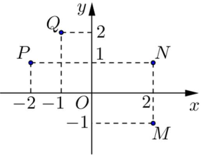
Điểm nào trong hình vẽ bên là điểm biểu diễn số phức \(z =  - 1 + 2i\) ?

Trong không gian Oxyz, cho mặt phẳng \(\left( P \right):x - 3y + 2z - 5 = 0\) và hai điểm \(A\left( {2;4;1} \right)\),\(B\left( { - 1;1;3} \right)\). Viết phương trình mặt phẳng \(\left( Q \right)\) đi qua hai điểm \(A,\,\,B\) và vuông góc với mặt phẳng \(\left( P \right)\).

Trong không gian với hệ toạ độ $Oxyz$, cho hai mặt phẳng  $\left( P \right):x + 2y + 2z + 11 = 0$  và  $\left( Q \right):x + 2y + 2z + 2 = 0$ . Tính khoảng cách giữa $\left( P \right)$ và $\left( Q \right)$.

Cho hai điểm \(A\left( {5;3;1} \right),B\left( {1;3;5} \right)\). Độ dài véc tơ \(\overrightarrow {AB} \) là:

Trong không gian với hệ tọa độ $Oxyz$, tìm tất cả các giá trị của $m$ để phương trình \({x^2} + {y^2} + {z^2} - 2x - 2y - 4z + m = 0\)  là phương trình của một mặt cầu.

Đề thi THPT QG – 2021 lần 1– mã 104

Trong không gian \(Oxyz,\) cho đường thẳng \(d:\dfrac{x}{1} = \dfrac{y}{{ - 1}} = \dfrac{{z - 1}}{2}\) và mặt phẳng \(\left( P \right):x + 2y - 2z + 2 = 0\). Hình chiếu vuông góc của \(d\) trên \(\left( P \right)\) là đường thẳng có phương trình: 

Cho tam giác $ABC$ biết $A\left( {2;4; - 3} \right)$ và trọng tâm $G$ của tam giác có toạ độ là $G\left( {2;1;0} \right)$. Khi đó \(\overrightarrow {AB}  + \overrightarrow {AC} \) có tọa độ là

Trong không gian Oxyz, tính khoảng cách giữa hai mặt phẳng\(\left( P \right):\,\,2x + 2y - z - 11 = 0\) và \(\left( Q \right):\,\,2x + 2y - z + 4 = 0\)

Trong không gian với hệ tọa độ \(Oxyz\), cho mặt phẳng \(\left( P \right):x + 2y - 3z + 4 = 0\) và đường thẳng \(d:\dfrac{{x + 2}}{1} = \dfrac{{y - 2}}{1} = \dfrac{z}{{ - 1}}\). Đường thẳng \(\Delta \) nằm trong \(\left( P \right)\) đồng thời cắt và vuông góc với \(d\) có phương trình:

Diện tích hình bình hành \(ABCD\) biết \(A\left( {1;2;3} \right),B\left( {0; - 1;1} \right)\) và \(C\left( { - 1;1;1} \right)\) là:

Cho hình chóp \(S.ABC\) có đáy là tam giác vuông cân tại\(A\), \(SA\) vuông góc với đáy. Biết \(SA = BC = a\), thể tích khối chóp \(S.ABC\) bằng:

Tìm các giá trị của tham số $m$ sao cho hàm số $y =  - {x^3} - {x^2} + mx + 1$ nghịch biến trên $R$?

Số điểm cực trị của hàm số \(y = \left| {\left( {x - 1} \right){{\left( {x - 2} \right)}^2}} \right|\) là:

Cho hàm số \(f\left( x \right)\) có \(f'\left( x \right) = {x^{2021}}{\left( {x - 1} \right)^{2020}}\left( {x + 1} \right)\)\(\forall x \in \mathbb{R}\). Hàm số đã cho có bao nhiêu điểm cực trị?

Tìm tất cả các giá trị của tham số \(m\) để hàm số \(y =  - {x^3} - 3{x^2} + mx + 2\) có cực đại và cực tiểu?

Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh bằng \(2a.\)  Tam giác \(SAB\) cân tại \(S\) và nằm trong mặt phẳng vuông góc với mặt đáy. Biết thể tích khối chóp \(S.ABCD\) bằng \(\dfrac{{4{a^3}}}{3}\) . Gọi \(\alpha \)  là góc giữa \(SC\) và mặt đáy, tính \(\tan \alpha .\)

Cho hàm số $y = {x^3} - 3{x^2} + 5x - 2$ có đồ thị $(C)$. Viết phương trình tiếp tuyến của đồ thị $(C)$ có hệ số góc nhỏ nhất.

Cho phương trình \({\log _7}\left( {{x^2} + 2x + 2} \right) + 1 > {\log _7}\left( {{x^2} + 6x + 5 + m} \right)\). Có tất cả bao nhiêu giá trị nguyên của tham số m để bất phương trình trên có tập nghiệm chứa khoảng \(\left( {1;3} \right)\)?

Cho hàm số \(y = f\left( x \right)\) có đồ thị trong hình sau:

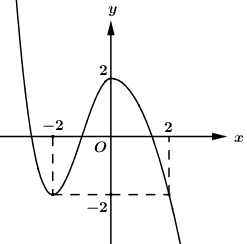
Số nghiệm của phương trình \(f\left( {{x^3} - 3x} \right) + 1 = 0\) trong khoảng \(\left( {0;2} \right)\) là: 

Cho hàm số $y = x + \dfrac{1}{x}.$ Giá trị nhỏ nhất của hàm số trên khoảng $\left( {0;\, + \infty } \right)$ là: