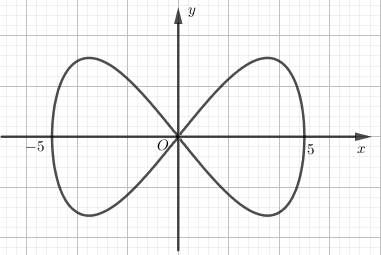
Trong Công viên Toán học có những mảnh đất hình dáng khác nhau. Mỗi mảnh được trồng một loài hoa và nó được tạo thành bởi một trong những đường cong đẹp nhất trong toán học. Ở đó có mảnh đất mang tên Bernoulli, nó được tạo thành từ đường Lemniscate có phương trình trong hệ tọa độ $Oxy$ là \(16{y^2} = {x^2}\left( {25 - {x^2}} \right)\) như hình vẽ bên. Tính diện tích $S$ của mảnh đất Bernoulli biết rằng mỗi đơn vị trong hệ trục tọa độ $Oxy$ tương ứng với chiều dài $1$ mét

\(4,2\% \)

\(4,26\% \)

\(4,3\% \)

\(4,5\% \)

$\left[ \begin{array}{l}m = 1\\m = 2\end{array} \right.$      

$\left[ \begin{array}{l}m < 1\\m > 2\end{array} \right.$

$1 < m < 2$

Không xác định được

$\dfrac{a}{{\sqrt 3 }}.$ 

$\dfrac{{2a}}{{\sqrt 3 }}.$

$\dfrac{a}{3}.$

$\dfrac{{\sqrt{3}a}}{2}.$

\(\left( {x;y} \right) = \left( { - 3 - \sqrt 3 ; - 2 + \sqrt 3 } \right)\) \(\left( {x;y} \right) = \left( { - 3 + \sqrt 3 ; - 2 - \sqrt 3 } \right)\).

\(\left( {x;y} \right) = \left( { - 3 - \sqrt 3 ; - 3 + \sqrt 3 } \right);\) \(\left( {x;y} \right) = \left( { - 2 - \sqrt 3 ; - 2 + \sqrt 3 } \right)\).

\(\left( {x;y} \right) = \left( { - 3; - 2} \right);\) \(\left( {x;y} \right) = \left( {3;2} \right)\)

\(\left( {x;y} \right) = \left( { - 3;3} \right);\) \(\left( {x;y} \right) = \left( {2;2} \right)\).

\(x \in \left[ { - \dfrac{1}{3};\dfrac{1}{3}} \right].\)

\(x \in \left( { - \infty ; - \dfrac{1}{3}} \right) \cup \left( {\dfrac{1}{3}; + \infty } \right).\)

\(x \in \left( { - \infty ; - \dfrac{1}{3}} \right] \cup \left[ {\dfrac{1}{3}; + \infty } \right).\)

\(x \in \left( { - \dfrac{1}{3};\dfrac{1}{3}} \right).\)

\({(x - 2)^2} + {(y - 1)^2} = 17\)

\({(x - 2)^2} + {(y - 1)^2} = 2\sqrt 5 \)

\({(x - 4)^2} + {(y - 2)^2} = 17\)

\({(x + 2)^2} + {(y + 1)^2} = 17\)