Số điểm cực trị của hàm số \(y = \left| {\left( {x - 1} \right){{\left( {x - 2} \right)}^2}} \right|\) là:
Trả lời bởi giáo viên
Xét hàm số \(y = \left( {x - 1} \right){\left( {x - 2} \right)^2} = {x^3} - 5{x^2} + 8x - 4\).
TXĐ: \(D = \mathbb{R}\).
Ta có \(y' = 3{x^2} - 10x + 8\).
\(y' = 0 \Leftrightarrow 3{x^2} - 10x + 8 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = \dfrac{4}{3}\end{array} \right.\)
BBT:
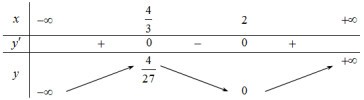
Từ BBT của đồ thị hàm số \(y = \left( {x - 1} \right){\left( {x - 2} \right)^2}\) ta suy ra BBT của đồ thị hàm số \(y = \left| {\left( {x - 1} \right){{\left( {x - 2} \right)}^2}} \right|\) như sau:
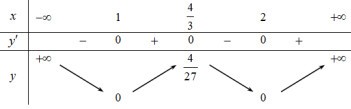
Từ BBT ta thấy hàm số \(y = \left| {\left( {x - 1} \right){{\left( {x - 2} \right)}^2}} \right|\) có 3 điểm cực trị.
Hướng dẫn giải:
- Xét hàm số \(y = \left( {x - 1} \right){\left( {x - 2} \right)^2}\), lập BBT của đồ thị hàm số.
- Từ đó suy ra BBT của đồ thị hàm số \(y = \left| {\left( {x - 1} \right){{\left( {x - 2} \right)}^2}} \right|\) từ đồ thị hàm số \(y = \left( {x - 1} \right){\left( {x - 2} \right)^2}\) bằng cách giữ nguyên phần đồ thị phía trên trục hoành, lấy đối xứng phần đồ thị phía dưới trục hoành qua trục hoành và xóa đi phần đồ thị phía dưới trục hoành.
- Từ BBT của đồ thị hàm số \(y = \left| {\left( {x - 1} \right){{\left( {x - 2} \right)}^2}} \right|\) suy ra số điểm cực trị của hàm số.
Câu hỏi khác
Cho biểu thức \(f\left( x \right) = 9{x^2} - 1.\) Tập hợp tất cả các giá trị của \(x\) để \(f\left( x \right) < 0\) là
\(x \in \left( { - \infty ; - \dfrac{1}{3}} \right) \cup \left( {\dfrac{1}{3}; + \infty } \right).\)
- Đề thi tư duy định lượng - Đề số 1 đánh giá năng lực ĐHQG Hà Nội có lời giải chi tiết
- Đề thi tư duy định lượng - Đề số 2 đánh giá năng lực ĐHQG Hà Nội có lời giải chi tiết
- Đề thi tư duy định lượng - Đề số 4 đánh giá năng lực ĐHQG Hà Nội có lời giải chi tiết
- Đề thi tư duy định lượng - Đề số 5 đánh giá năng lực ĐHQG Hà Nội có lời giải chi tiết
- Đề thi tư duy định lượng - Đề số 11 đánh giá năng lực ĐHQG Hà Nội có lời giải chi tiết
