Cho hình chóp \(S.ABC\) có đáy là tam giác vuông cân tại\(A\), \(SA\) vuông góc với đáy. Biết \(SA = BC = a\), thể tích khối chóp \(S.ABC\) bằng:
Trả lời bởi giáo viên
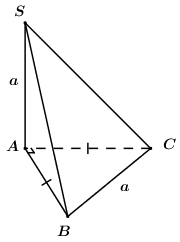
Ta có tam giác \(ABC\) vuông cân tại \(A\) và \(BC = a\) \( \Rightarrow AB = AC = \dfrac{a}{{\sqrt 2 }}\).
Khi đó \({S_{ABC}} = \dfrac{1}{2}AB.AC = \dfrac{1}{2}.\dfrac{a}{{\sqrt 2 }}.\dfrac{a}{{\sqrt 2 }} = \dfrac{{{a^2}}}{4}\).
Vậy thể tích khối chóp \(S.ABC\) là \({V_{S.ABC}} = \dfrac{1}{3}SA.{S_{\Delta ABC}} = \dfrac{1}{3}.a.\dfrac{{{a^2}}}{4} = \dfrac{{{a^3}}}{{12}}.\)
Hướng dẫn giải:
- Sử dụng tính chất tam giác vuông cân: cạnh góc vuông = cạnh huyền : \(\sqrt 2 \), tính độ dài 2 cạnh góc vuông, từ đó tính diện tích đáy.
- Tính thể tích khối chóp: \({V_{S.ABC}} = \dfrac{1}{3}SA.{S_{\Delta ABC}}\).
Câu hỏi khác
Cho biểu thức \(f\left( x \right) = 9{x^2} - 1.\) Tập hợp tất cả các giá trị của \(x\) để \(f\left( x \right) < 0\) là
\(x \in \left( { - \infty ; - \dfrac{1}{3}} \right) \cup \left( {\dfrac{1}{3}; + \infty } \right).\)


