Đề thi tư duy định lượng - Đề số 9

Dựa vào các thông tin dưới đây để trả lời câu hỏi:

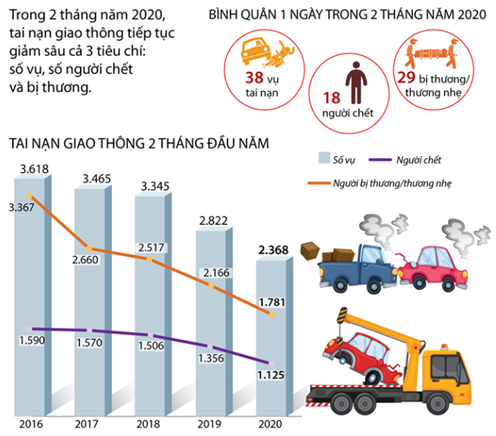
Số vụ tai nạn năm 2020 trong hai tháng đầu năm giảm bao nhiêu vụ?

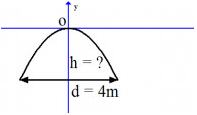
Một cái cổng hình parabol có dạng \(y =  - \dfrac{1}{2}{x^2}\) có chiều rộng \(d = 4m.\)

Tính chiều cao \(h\) của cổng (xem hình minh họa)

Cho hình chóp $S.ABCD$, có đáy $ABCD$ là hình chữ nhật. Cạnh bên $SA$ vuông góc với đáy, $SA = AB = a$ và $AD = x.a$. Gọi $E$ là trung điểm của $SC$. Tìm $x$, biết khoảng cách từ điểm $E$ đến mặt phẳng $\left( {SBD} \right)$ bằng $h = \dfrac{a}{3}$.

Cho hệ phương trình \(\left\{ \begin{array}{l}{x^2} + 2xy + 8x = 3{y^2} + 12y + 9\\{x^2} + 4y + 18 - 6\sqrt {x + 7}  - 2x\sqrt {3y + 1}  = 0\end{array} \right.\) có nghiệm là $\left( {a;b} \right)$. Khi đó giá trị biểu thức \(T = 5{a^2} + 4{b^2}\)

Cho biểu thức \(f\left( x \right) = \left( {x + 5} \right)\left( {3 - x} \right).\) Tập hợp tất cả các giá trị của \(x\) thỏa mãn bất phương trình \(f\left( x \right) \le 0\) là

Cho đường thẳng đi qua hai điểm \(A\left( {3,0} \right)\), \(B\left( {0;4} \right)\). Tìm tọa độ điểm \(M\) nằm trên \(Oy\) sao cho diện tích tam giác \(MAB\) bằng \(6\)

Cho phương trình ${x^2} + {y^2} - 2mx - 4\left( {m - 2} \right)y + 6 - m = 0{\rm{   }}\left( 1 \right)$. Tìm điều kiện của $m$ để $\left( 1 \right)$ là phương trình đường tròn.

Nghiệm của phương trình \({\sin ^2}x-\sin x = 0\) thỏa điều kiện: \(0 < x < \pi \).

Một cơ sở khoan giếng đưa ra định mức giá như sau: Giá của mét khoản đầu tiên là 10000 đồng và kể từ mét khoan thứ hai, giá của mỗi mét sau tăng thêm 3000 đồng so với giá của mét khoan ngay trước đó. Một người muốn ký hợp đồng với cơ sở khoan giếng này để khoan một giếng sâu 100 mét lấy nước dùng cho sinh hoạt của gia đình. Hỏi sau khi hoàn thành việc khoan giếng, gia đình đó phải thanh toán cho cơ sở khoan giếng số tiền bằng bao nhiêu?

Một nhóm gồm 2 học sinh lớp 10, 2 học sinh lớp 11 và 2 học sinh lớp 12 xếp thành hai hàng ngang để chụp ảnh, mỗi hàng 3 người. Gọi n là số cách xếp sao cho 2 học sinh lớp 10 đứng ở hàng phía trước và 2 học sinh lớp 12 đứng ở hàng phía sau. Tính n.

Xác suất bắn trúng đích của một người bắn súng là $0,6$. Xác suất để trong ba lần bắn độc lập người đó bắn trúng đích đúng một lần.

Cho hàm số \(f\left( x \right)\) xác định trên \(\mathbb{R}\) thỏa mãn\(\mathop {\lim }\limits_{x \to 2} \dfrac{{f\left( x \right) - 16}}{{x - 2}} = 12.\) Giới hạn \(\mathop {\lim }\limits_{x \to 2} \dfrac{{\sqrt {2f\left( x \right) - 16}  - 4}}{{{x^2} + x - 6}}\) bằng $\dfrac{a}{b}$(phân số tối giản). Tổng $a^2+b^2$ bằng:

Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên  \(\mathbb{R}\) Xét các hàm số \(g\left( x \right) = f\left( x \right) - f\left( {2x} \right)\) và \(h\left( x \right) = f\left( x \right) - f\left( {4x} \right)\). Biết rằng \(g'\left( 1 \right) = 21\)  và \(g'\left( 2 \right) = 1000\). Tính \(h'\left( 1 \right)\)

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang có cạnh đáy $AB$ và $CD$ . Gọi I, J lần lượt là trung điểm của các cạnh $AD$  và $BC$  và $G$  là trọng tâm tam giác $SAB$. Tìm điều kiện của $AB$  và $CD$  để thiết diện của $\left( {IJG} \right)$ và hình chóp là một hình bình hành.

Cho hình chóp \(S.ABCD\), với đáy \(ABCD\) là hình bình hành tâm \(O;AD,SA,AB\) đôi một vuông góc \(AD = 8,SA = 6\). \((P)\)là mặt phẳng qua trung điểm của \(AB\) và vuông góc với \(AB\). Thiết diện của \((P)\) và hình chóp có diện tích bằng?

Cho hàm số \(f\left( x \right)\) xác định trên \(\mathbb{R}\backslash \left\{ {\frac{1}{2}} \right\}\) thỏa mãn \(f'\left( x \right) = \frac{2}{{2x - 1}};f\left( 0 \right) = 1,f\left( 1 \right) = 2\). Giá trị của biểu thức \(f\left( { - 1} \right) + f\left( 3 \right)\) bằng:

Sàn của một viện bảo tàng mỹ thuật được lát bằng những viên gạch hình vuông cạnh \(40\,\left( {cm} \right)\) như hình bên. Biết rằng người thiết kế đã sử dụng các đường cong có phương trình \(4{x^2} = {y^4}\) và \(4{\left( {\left| x \right| - 1} \right)^3} = {y^2}\) để tạo hoa văn cho viên gạch. Diện tích phần được tô đậm gần nhất với giá trị nào dưới đây?

Cho hàm số \(f(x)\) liên tục trên \(\left[ { - 1;2} \right]\)và thỏa mãn điều kiện \(f(x) = \sqrt {x + 2}  + xf\left( {3 - {x^2}} \right)\). Tính tích phân \(I = \int\limits_{ - 1}^2 {f(x)dx} \).

Biết rằng \(\int\limits_{1}^{e}{x\ln xdx}=a{{e}^{2}}+b,\,\,\,\,a,b\in \mathbb{Q}\). Tính $a + b$.

Cho (H) là hình phẳng giới hạn bởi đồ thị hàm số \(y=\sqrt{x},\) trục hoành và đường thẳng \(x=9.\) Khi (H) quay quanh trục Ox tạo thành một khối tròn xoay có thể tích bằng:

Bạn An gửi tiết kiệm vào ngân hàng với số tiền là $1.000.000$ đồng không kì hạn với lãi suất là $0,65\% $ mỗi tháng. Tính số tiền bạn An nhận được sau $2$ năm?

Giải bất phương trình: $\log _2^2x - 4033{\log _2}x + 4066272 \le 0$ .

Phương trình \({\log _3}\left( {3x + 6} \right) = 4\) có nghiệm là

Phương trình \({\log _3}\left( {{x^2} - 9} \right) = 2\) có các nghiệm là

Tìm $m$ để $({C_m})$ : $y = {x^4} - 2m{x^2} + 2$ có $3$ điểm cực trị là $3$ đỉnh của một tam giác vuông cân.

Giá trị nhỏ nhất của hàm số \(y = {x^2} - 4x + 5\) là?

Khối chóp có đáy là hình bình hành, một cạnh đáy bằng \(a\) và các cạnh bên đều bằng \(a\sqrt 2 \). Thể tích của khối chóp có giá trị lớn nhất là:

Cho hai số phức \({z_1} = 1 + 2i\) và \({z_2} = 3 - 4i.\) Số phức \(2{z_1} + 3{z_2}\) là số phức nào sau đây?

Trên mặt phẳng tọa độ \(Oxy\), tìm tập hợp các điểm biểu diễn các số phức \(z\) thỏa mãn điều kiện \(\left| {z - 2} \right| + \left| {z + 2} \right| = 10\).

Cho các số phức \({z_1} = 2,{z_2} =  - 4i,{z_3} = 2 - 4i\) có điểm biểu diễn tương ứng trên mặt phẳng tọa độ Oxy là A, B, C. Diện tích tam giác ABC bằng

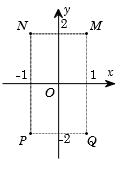
Giả sử $M,\,\,N,\,\,P,\,\,Q$ được cho ở hình vẽ bên là điểm biểu diễn của các số phức ${z_1},\,\,{z_2},\,\,{z_3},\,\,{z_4}$ trên mặt phẳng tọa độ. Khẳng định nào sau đây là đúng?

Trong không gian với hệ trục tọa độ Oxyz, cho 2 điểm \(A(2;1;0),\,\,B(1;-1;3)\). Mặt phẳng qua AB và vuông góc với mặt phẳng (P): \(x+3y-2z-1=0\) có phương trình là

Đề thi THPT QG - 2021 - mã 102

Trong không gian \(Oxyz,\) cho hai đểm \(A\left( {0;0;1} \right)\) và \(B\left( {2;1;3} \right)\). Mặt phẳng đi qua \(A\) và vuông góc với \(AB\) có phương trình là:  

Cho hai véc tơ \(\overrightarrow u  = \left( { - 1; - 1; - 1} \right),\overrightarrow v  = \left( {2;1;0} \right)\), khi đó cô sin của góc hợp bởi hai véc tơ đó là:

Trong không gian $Oxyz$, cho hai mặt phẳng \((\alpha ):x - my + z + 6m + 3 = 0\) và \((\beta ):mx + y - mz + 3m - 8 = 0\); hai mặt phẳng này cắt nhau theo giao tuyến là đường thẳng \(\Delta \). Gọi \({\Delta ^\prime }\) là hình chiếu của \(\Delta \) lên mặt phẳng $Oxy$. Biết rằng khi \(m\) thay đổi thì đường thẳng \({\Delta ^\prime }\) luôn tiếp xúc với một mặt cầu cố định có tâm \(I(a;b;c)\) thuộc mặt phẳng $Oxy$. Tính giá trị biểu thức \(P = 10{a^2} - {b^2} + 3{c^2}\).

Trong không gian với hệ tọa độ \(Oxyz\), cho đường thẳng \(d:\left\{ \begin{array}{l}x =  - \dfrac{9}{5} - t\\y = 5t\\z = \dfrac{7}{5} + 3t\end{array} \right.\) và mặt phẳng \(\left( P \right):3x - 2y + 3z - 1 = 0\).

Gọi \(d'\) là hình chiếu của \(d\) trên mặt phẳng \(\left( P \right)\). Trong các vectơ sau, vectơ nào không phải là vectơ chỉ phương của \(d'\)?

Cho hình bình hành $ABCD$ với $A\left( {2;4; - 4} \right),B\left( {1;1; - 3} \right),C\left( { - 2;0;5} \right),D\left( { - 1;3;4} \right)$. Diện tích của hình bình hành $ABCD$ bằng

Trong không gian Oxyz, cho điểm A(-1;3;-2) và mặt phẳng \(\left( \alpha  \right):\,x-2y-2z+5=0\). Khoảng cách từ điểm A đến mặt phẳng \(\left( \alpha  \right)\) bằng:

Trong không gian với hệ tọa độ $Oxyz$ cho mặt phẳng $(P):x - y + 3z + 2 = 0$ và đường thẳng $(d):\dfrac{{x - 2}}{1} = \dfrac{{y + 1}}{2} = \dfrac{{z - 1}}{3}$. Phương trình mặt phẳng $(Q)$ chứa đường thẳng $d$ và vuông góc với $(P)$ là:

Cho tứ diện \(ABCD\), biết \(A\left( {1;2;0} \right),B\left( {0;1; - 1} \right),C\left( {0;0;1} \right)\) và \(G\left( {2; - 1;0} \right)\) là trọng tâm tứ diện. Thể tích khối tứ diện đã cho là:

Cho hình lăng trụ $ABC.A’B’C’$ có độ dài tất cả các cạnh bằng $a$ và hình chiếu vuông góc của đỉnh $C$ trên $(ABB’A’)$ là tâm của hình bình hành $ABB’A’$. Thể tích của khối lăng trụ là:

Tập hợp các giá trị của tham số  \(m\)  để hàm số  \(y = 2{x^2} - mx + m\) đồng biến trên khoảng  \(\left( {1; + \infty } \right)\) là

Đề mẫu ĐGNL HN 2021

Hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = {x^3} - \dfrac{{29}}{8}{x^2} + \dfrac{9}{4}x + \dfrac{3}{8}\), \(\forall x\, \in \,\mathbb{R}\). Gọi \(S\) là tập hợp các điểm cực tiểu của hàm số \(g\left( x \right) = f\left( {2x + 1} \right) - {x^3}.\) Tổng giá trị các phần tử của \(S\) bằng

Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) là \(f'\left( x \right) = \left( {{x^2} - 3x} \right)\left( {{x^3} - 4x} \right).\)  Điểm cực đại của hàm số đã cho là:

Với tất cả giá trị nào của \(m\) thì hàm số \(y = m{x^4} + \left( {m - 1} \right){x^2} + 1 - 2m\) chỉ có một cực trị

Cho hình chóp \(S.ABC\) đáy \(ABC\) là tam giác vuông tại \(A,AB = a,AC = a\sqrt 3 \). Tam giác $SBC$ đều nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp $S.ABC$

Có bao nhiêu tiếp tuyến với đồ thị $\left( C \right):y = {x^4} - 2{x^2}$ đi qua gốc tọa độ $O$?

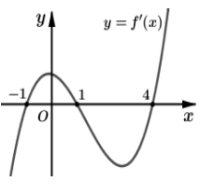
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị \(f'\left( x \right)\) như hình vẽ bên. Bất phương trình \({\log _5}\left[ {f\left( x \right) + m + 2} \right] + f\left( x \right) > 4 - m\) đúng với mọi \(x \in \left( { - 1;4} \right)\) khi và chỉ khi

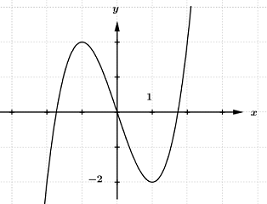
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Với các giá trị nào của tham số m thì phương trình  \(f\left( {\left| x \right|} \right) = 3m + 1\) có bốn nghiệm phân biệt.

Giá trị lớn nhất của hàm số $f\left( {\text{x}} \right) = \dfrac{{6 - 8{\text{x}}}}{{{x^2} + 1}}$ trên tập xác định của nó là: