Giá trị lớn nhất của hàm số $f\left( {\text{x}} \right) = \dfrac{{6 - 8{\text{x}}}}{{{x^2} + 1}}$ trên tập xác định của nó là:
Trả lời bởi giáo viên
TXĐ: $D=R$
Ta có: $f'\left( x \right) = \dfrac{{8{{\text{x}}^2} - 12{\text{x}} - 8}}{{{{\left( {{x^2} + 1} \right)}^2}}}$
$f'\left( x \right) = 0 \Leftrightarrow x = 2$ hoặc $x = - \dfrac{1}{2}$
$\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to - \infty } y = 0$
Bảng biến thiên
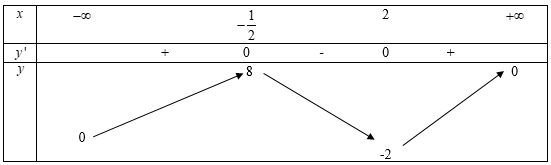
Vậy giá trị lớn nhất của hàm số là $y = 8$ tại $x = - \dfrac{1}{2}$
Hướng dẫn giải:
Khảo sát hàm số $y = f\left( x \right)$ trên TXĐ và rút ra kết luận.
Giải thích thêm:
Cần phải tính giới hạn của hàm số khi $x \to \pm \infty $ để tìm được GTLN của hàm số. Nhiều HS không tìm hai giới hạn trên mà vội vàng kết luận $y = 8$ là GTLN là chưa logic vì nếu tìm được một trong hai giới hạn tiến ra $ + \infty $ thì lúc này hàm số sẽ không có GTLN trên $R$.
Câu hỏi khác
- Đề thi tư duy định lượng - Đề số 1 đánh giá năng lực ĐHQG Hà Nội có lời giải chi tiết
- Đề thi tư duy định lượng - Đề số 2 đánh giá năng lực ĐHQG Hà Nội có lời giải chi tiết
- Đề thi tư duy định lượng - Đề số 4 đánh giá năng lực ĐHQG Hà Nội có lời giải chi tiết
- Đề thi tư duy định lượng - Đề số 5 đánh giá năng lực ĐHQG Hà Nội có lời giải chi tiết
- Đề thi tư duy định lượng - Đề số 11 đánh giá năng lực ĐHQG Hà Nội có lời giải chi tiết
