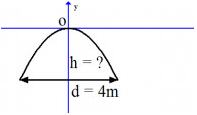
Một cái cổng hình parabol có dạng \(y = - \dfrac{1}{2}{x^2}\) có chiều rộng \(d = 4m.\)
Tính chiều cao \(h\) của cổng (xem hình minh họa)
Đáp án: \(h = \)
$m$
Trả lời bởi giáo viên
Đáp án: \(h = \)
$m$
Bước 1:
Gọi hai điểm chân cổng là \(A\left( {{x_A};{y_A}} \right)\) và \(B\left( {{x_B};{y_B}} \right)\) thì ta có \({y_A} = {y_B}\) và \(\left| {{x_A}} \right| = \left| {{x_B}} \right|.\)
Vì \(d = 4\) nên \(\left| {{x_A}} \right| = \left| {{x_B}} \right| = 2.\)
Bước 2: Tính $h$
Vậy \(h = \left| {{y_A}} \right| = \left| { - \dfrac{1}{2}x_A^2} \right| = \left| { - \dfrac{1}{2}{{.2}^2}} \right| = 2\,\left( m \right).\)
Hướng dẫn giải:
Sử dụng tính đối xứng của parabol
Bước 1: Gọi hai điểm chân cổng là \(A\left( {{x_A};{y_A}} \right)\) và \(B\left( {{x_B};{y_B}} \right)\). Tính $\left| {{x_A}} \right| $ và $ \left| {{x_B}} \right|$
Bước 2: Tính $h$