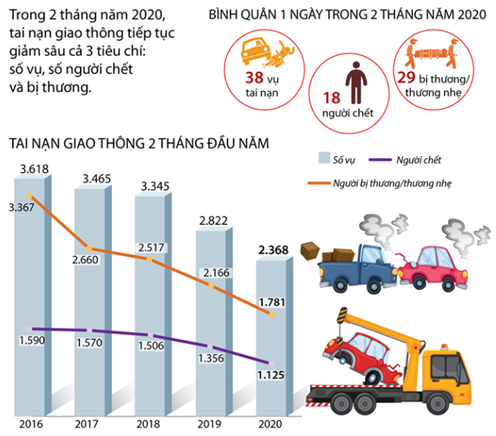
Trong không gian $Oxyz$, cho hai mặt phẳng \((\alpha ):x - my + z + 6m + 3 = 0\) và \((\beta ):mx + y - mz + 3m - 8 = 0\); hai mặt phẳng này cắt nhau theo giao tuyến là đường thẳng \(\Delta \). Gọi \({\Delta ^\prime }\) là hình chiếu của \(\Delta \) lên mặt phẳng $Oxy$. Biết rằng khi \(m\) thay đổi thì đường thẳng \({\Delta ^\prime }\) luôn tiếp xúc với một mặt cầu cố định có tâm \(I(a;b;c)\) thuộc mặt phẳng $Oxy$. Tính giá trị biểu thức \(P = 10{a^2} - {b^2} + 3{c^2}\).

Bước 1: Biểu diễn M và vectơ chỉ phương của \(\Delta \) theo m.

Mặt phẳng \((\alpha ):x - my + z + 6m - 3z = 0\) có một vectơ pháp tuyến là \(\overrightarrow {{n_1}}  = (1; - m;1)\), và mặt phẳng \((\beta ):mx + y - mz + 3m - 8 = (\alpha ) \cap (\beta )\). \(\overrightarrow {{n_1}}  = (1; - m;1)\), và mặt phẳng \((\beta ):mx + y - mz\) có một vectơ pháp tuyến là \(\overrightarrow {{n_2}}  = (m;1; - m).\) Ta có \(M\left( { - 3m + \dfrac{4}{m} - 3;0; - 3m - \dfrac{4}{m}} \right) \in \Delta  = \left( \alpha  \right) \cap \left( \beta  \right)\)

Do đó \(\Delta \) có một vectơ chỉ phương là \(\vec u = \left[ {\overrightarrow {{n_1}} ;\overrightarrow {{n_2}} } \right] = \left( {{m^2} - 1;2m;{m^2} + 1} \right)\).

Bước 2: Gọi \((P)\) là mặt phẳng chứa đường thẳng \(\Delta \) và vuông góc với mặt phẳng \((Oxy)\). Tìm c.

Gọi \((P)\) là mặt phẳng chứa đường thẳng \(\Delta \) và vuông góc với mặt phẳng \((Oxy)\). Khi đó \((P)\) có một vectơ pháp tuyến là \(\vec n = [\vec u;\vec k] = \left( {2m;1 - {m^2};0} \right)\).

Phương trình mặt phẳng \((P)\) là : \(2mx + \left( {1 - {m^2}} \right)y + 6{m^2} + 6m - 8 = 0\).

Vì \(I(a;b;c) \in (Oxy)\) nên \(I(a;b;0)\).

Bước 3: Theo giả thiết ta suy ra \((P)\) là tiếp diện của mặt cầu \((S) \Rightarrow d(I;(P)) = R\). Tìm a và b

Theo giả thiết ta suy ra \((P)\) là tiếp diện của mặt cầu \((S) \Rightarrow d(I;(P)) = R\)

\( \Leftrightarrow \dfrac{{\left| {2ma + \left( {1 - {m^2}} \right)b + 6{m^2} + 6m - 8} \right|}}{{\sqrt {4{m^2} + {{\left( {1 - {m^2}} \right)}^2}} }} = R > 0\)

\( \Leftrightarrow \dfrac{{\left| {2m(a + 3) + (6 - b){m^2} + b - 8} \right|}}{{{m^2} + 1}} = R > 0\)

\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{2m(a + 3) + (6 - b){m^2} + b - 8 = R\left( {{m^2} + 1} \right)}\\{2m(a + 3) + (6 - b){m^2} + b - 8 =  - R\left( {{m^2} + 1} \right)}\end{array}} \right.\)

\( \Leftrightarrow \left[ \begin{array}{l}\left\{ {\begin{array}{*{20}{l}}{2(a + 3) = 0}\\{6 - b = R}\\{b - 8 = R}\\{R > 0}\end{array}} \right.\\\left\{ \begin{array}{l}2(a + 3) = 0\\6 - b =  - R\\b - 8 =  - R\\R > 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ {\begin{array}{*{20}{l}}{a =  - 3 = 0}\\{6 - b = b - 8}\\{ - R = 6 - b < 0}\end{array}} \right.\\\left\{ {\begin{array}{*{20}{l}}{a =  - 3}\\{6 - b = b - 8}\\{R = 6 - b > 0}\end{array}} \right.\end{array} \right.\)

\( \Rightarrow \left\{ \begin{array}{l}a =  - 3\\b = 7\end{array} \right.\)

Vậy \(I( - 3;7;0)\), do đó \(P = 10{a^2} - {b^2} + 3{c^2} = 41\).