Đề minh họa ĐGNL ĐHQG HN năm 2021
Kỳ thi ĐGNL ĐHQG Hà Nội
Kết quả:
0/50
Thời gian làm bài: 00:00:00
Hình vẽ dưới đây mô tả số người nhiễm Covid-19 đang được điều trị ở Việt Nam tính từ ngày 23/01/2020 đến ngày 13/02/2021.
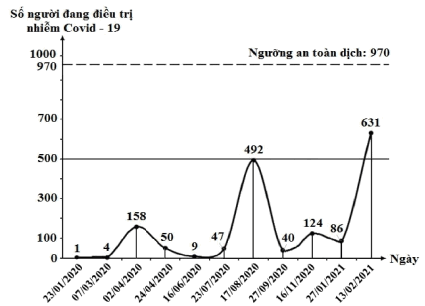
Hỏi từ ngày 16/06/2020 đến ngày 27/01/2021, ngày nào Việt Nam có số người được điều trị Covid-19 nhiều nhất?
Một vật rơi tự do theo phương thẳng đứng có quãng đường dịch chuyển \(S\left( t \right) = \dfrac{1}{2}g{t^2}\) với t là thời gian tính bằng giây (s) kể từ lúc vật bắt đầu rơi, S là quãng đường tính bằng mét \(\left( m \right),\,\,\;g{\rm{ = }}9,8{\rm{ }}m/{s^2}.\) Vận tốc tức thời của vật tại thời điểm \(t=4s\) là
Phương trình \({\log _3}\left( {3x + 6} \right) = 4\) có nghiệm là
Hệ phương trình sau có bao nhiêu nghiệm? \(\left\{ \begin{array}{l}{y^2} + \left| y \right| = 0\\{y^2} + {x^2} - 8x = 0\end{array} \right.\)
Trên mặt phẳng tọa độ Oxy, gọi M , N , P theo thứ tự là các điểm biểu diễn các số phức \({z_1} = 3 - 2i,\)\({z_2} = 5 - 10i,\,{z_3} = 10 + 3i\). Tọa độ trọng tâm của tam giác MNP là
Trong không gian Oxyz, mặt phẳng ( P) đi qua điểm \(M\left( {2; - 3;4} \right)\) và vuông góc với trục Oy có phương trình là
Trong không gian Oxyz, cho điểm \(M\left( {1;2;3} \right)\). Tìm tọa độ điểm \(M'\) đối xứng với \(M\) qua trục \(Oz\).
Bất phương trình \(\dfrac{2}{{x + 1}} > \dfrac{5}{{x - 2}}\) có số nghiệm nguyên thuộc đoạn \(\left[ {0;10} \right]\) là
Số nghiệm của phương trình \(\sin \,x\, + \sqrt 3 \,\cos \,x = 2\sin \,2x\) thuộc khoảng \(\left( {0;2\pi } \right)\) là
Một người làm việc cho một công ty. Theo hợp đồng trong năm đầu tiên, tháng lương thứ nhất là 6 triệu đồng và lương tháng sau cao hơn tháng trước là 200 ngàn đồng. Hỏi theo hợp đồng tháng thứ 7 người đó nhận được lương là bao nhiêu?
Họ nguyên hàm của hàm số \(f\left( x \right) = \dfrac{1}{{{x^2} - 2x}}\) trên khoảng \(\left( {2; + \infty } \right)\) là
Cho hàm số \(f\left( x \right)\) có bảng biến thiên như hình vẽ:
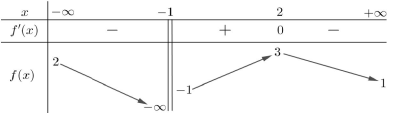
Tìm điều kiện của tham số \(m\) để \(m < f\left( x \right) + {x^2}\) với mọi \(x \in \left( {1;2} \right)\).
Một chất điểm chuyển động thẳng với vận tốc\(v\left( t \right) = 2t + 3\,\left( {m/s} \right)\), với \(t\) là thời gian tính bằng giây \(\left( s \right)\) từ lúc chất điểm bắt đầu chuyển động. Tính quãng đường chất điểm đi được trong khoảng thời gian từ giây thứ nhất đến giây thứ năm.
Một thiết bị trong năm 2021 được định giá 100 triệu đồng. Trong 5 năm tiếp theo, mỗi năm giá trị thiết bị giảm 6 % so với năm trước và từ năm thứ 6 trở đi, mỗi năm giá trị thiết bị giảm 10 % so với năm trước. Hỏi bắt đầu từ năm nào thì giá trị thiết bị nhỏ hơn 50 triệu đồng?
Tập nghiệm của bất phương trình \({\log _{\frac{2}{3}}}\,\left( {3x - 2} \right) > \,{\log _{\frac{2}{3}}}\left( {2x+ 1} \right)\) là
Cho \(\left( H \right)\) là hình phẳng giới hạn bởi các đường \(y = \sqrt x \) và \(y = {x^2}.\) Thể tích của khối tròn xoay tạo thành khi quay hình \(\left( H \right)\) quanh trục \(Ox\) bằng
Tập hợp các giá trị của tham số \(m\) để hàm số \(y = 2{x^2} - mx + m\) đồng biến trên khoảng \(\left( {1; + \infty } \right)\) là
Phương trình \(\left( {3 + 2i} \right)z - \left( {4 + 9i} \right) = 2 - 5i\) có nghiệm là
Xét các số phức \(z\) thỏa mãn \(\left| {z + 2 + i} \right| = \left| {\overline z + i} \right|\). Tập hợp điểm biểu diễn các số phức \(z\) là đường thẳng có phương trình
Trên mặt phẳng tọa độ\(Oxy\), cho tam giác \(ABC\) có tọa độ các đỉnh là \(A\left( {2;3} \right),{\rm{ }}B\left( {5;0} \right)\) và \(C\left( { - 1;0} \right)\). Tìm tọa độ điểm \(M\) thuộc cạnh \(BC\) sao cho diện tích tam giác \(MAB\) bằng hai lần diện tích tam giác \(MAC\)
Trên mặt phẳng tọa độ \(Oxy,\) cho đường tròn \(\left( {{C_m}} \right):\,\,\,{x^2} + {y^2} - 6x - 2my + 6m - 16 = 0\), với \(m\) là tham số thực. Khi \(m\) thay đổi, bán kính đường tròn \(\left( {{C_m}} \right)\) đạt giá trị nhỏ nhất bằng bao nhiêu?
Trong không gian \(Oxyz,\) mặt phẳng \(\left( P \right)\) đi qua hai điểm \(M\left( {3;1; - 1} \right),\,N\left( {2; - 1;4} \right)\) và vuông góc với mặt phẳng \(\left( Q \right):\,2x - y + 3z + 75 = 0\) có phương trình là
Cho khối nón có bán kính đáy bằng 3 và diện tích xung quanh bằng \(12\pi\). Hỏi thể tích của khối nón đã cho bằng bao nhiêu?
Tháp nước Hàng Đậu là một di tích kiến trúc cổ của Thủ đô Hà Nội, được xây dựng vào cuối thế kỉ XIX. Tháp được thiết kế gồm thân tháp có dạng hình trụ và phần mái phía trên dạng hình nón. Không gian bên trong toàn bộ tháp được minh họa theo hình vẽ với đường kính đáy hình trụ và đường kính đáy của hình nón đều bằng 19 m, chiều cao hình trụ 20 m, chiều cao hình nón là 5 m.
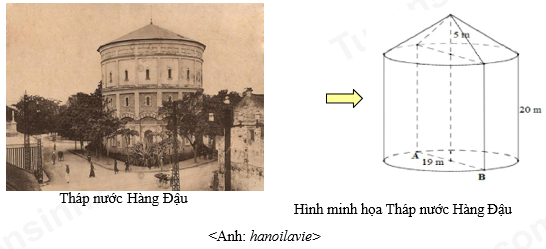
Thể tích của toàn bộ không gian bên trong tháp nước Hàng Đậu gần nhất với giá trị nào sau đây?
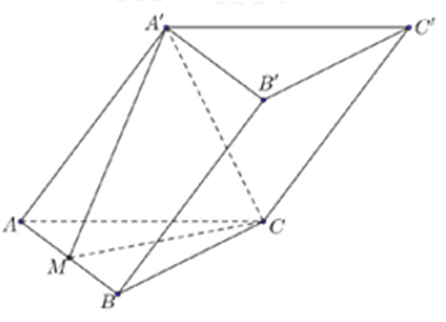
Cho lăng trụ \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác vuông cân tại \(C\). Gọi \(M\) là trung điểm của cạnh\(AB\). Biết rằng \(A'CM\) là tam giác đều cạnh \(a\) và nằm trong mặt phẳng vuông góc với mặt phẳng đáy (minh họa như hình vẽ). Thể tích của khối lăng trụ \(ABC.A'B'C'\) bằng
Cho hình chóp \(S.ABC{\rm{D}}\) có đáy \(ABC{\rm{D}}\) là hình bình hành. Gọi điểm \(M\) là điểm thuộc cạnh \(S{\rm{D}}\) sao cho \(SM = \dfrac{2}{3}SD\) (minh họa như hình vẽ). Mặt phẳng chứa \(AM\) và song song với \(B{\rm{D}}\) cắt cạnh \(SC\) tại \(K\). Tỷ số \(\dfrac{{SK}}{{SC}}\) bằng
Trong không gian \(Oxyz\), cho mặt cầu \(\left( C \right):\,\,\,{\left( {x + 1} \right)^2} + {\left( {y - 3} \right)^2} + {\left( {z - 2} \right)^2} = 1\) và hai điểm \(A\left( {2;1;0} \right)\), \(B\left( {0;2;0} \right)\). Khi điểm \(S\) thay đổi trên mặt cầu \(\left( C \right)\), thể tích của khối chóp \(S.OAB\) có giá trị lớn nhất bằng bao nhiêu?
Trong không gian \(Oxyz,\) gọi \(d'\) là hình chiếu vuông góc của đường thẳng \(d:\,\,\left\{ \begin{array}{l}x = t\\y = t\\z = t\end{array} \right.\) trên mặt phẳng \(\left( {Oxy} \right)\). Phương trình tham số của đường thẳng \(d'\) là
Đề mẫu ĐGNL HN 2021
Hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = {x^3} - \dfrac{{29}}{8}{x^2} + \dfrac{9}{4}x + \dfrac{3}{8}\), \(\forall x\, \in \,\mathbb{R}\). Gọi \(S\) là tập hợp các điểm cực tiểu của hàm số \(g\left( x \right) = f\left( {2x + 1} \right) - {x^3}.\) Tổng giá trị các phần tử của \(S\) bằng
Trong không gian \(Oxyz,\) cho hai điểm \(A\left( {4;0;4} \right)\) và \(B\left( {2;4;0} \right)\). Điểm \(M\) di động trên tia \(Oz\), điểm \(N\) di động trên tia \(Oy\). Đường gấp khúc \(AMNB\) có độ dài nhỏ nhất bằng bao nhiêu? (Kết quả làm tròn đến hàng phần chục).
Cho hàm số \(f\left( x \right) = \dfrac{1}{3}{x^3} + m{x^2} + \left( {{m^2} - 4} \right)x + 1\). Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y = f\left( {\left| x \right|} \right)\) có đúng 3 điểm cực trị?
Số giá trị nguyên của tham số \(m\) để phương trình \(\sqrt {{x^2} - mx + 3} = \sqrt {2x - 1} \) có hai nghiệm phân biệt là
Cho hàm số \(f\left( x \right)\) xác định và có đạo hàm trên khoảng \(\left( {0; + \infty } \right)\). Biết rằng \(2xf'\left( x \right) = f\left( x \right) + {x^2},\) \(\,\forall x \in \,\left( {0; + \infty } \right)\) và \(f\left( 1 \right) = 2\). Tính \(\int\limits_1^4 {f\left( x \right)d{\rm{x}}} \).
Một ngân hàng đề thi có 20 hạng mục, mỗi hạng mục có 10 câu hỏi. Đề thi có 20 câu hỏi tương ứng 20 hạng mục sao cho mỗi hạng mục có đúng 1 câu hỏi. Máy tính chọn từ ngân hàng ngẫu nhiên 2 đề thi thỏa mãn tiêu chí trên. Tìm xác suất để 2 đề thi có ít nhất 3 câu hỏi trùng nhau. (Kết quả làm tròn đến hàng phần nghìn.)
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Lấy \(M,\,N\) lần lượt là trung điểm các cạnh \(SB,\,SD;\,K\) là giao điểm của mặt phẳng \(\left( {AMN} \right)\) và \(SC.\) Gọi \({V_1}\) là thể tích của khối chóp \(S.AMKN\), \({V_2}\) là thể tích của khối đa diện lồi \(AMKNBCD\). Tính \(\dfrac{{{V_1}}}{{{V_2}}}.\)
Cho hàm số \(y = \dfrac{{x + 2}}{{x - 1}}\) có đồ thị là \(\left( C \right)\) tại điểm \(M\left( {2;4} \right)\) có hệ số góc bằng bao nhiêu?
Đáp án:
Đáp án:
Cho hàm số \(f\left( x \right)\) có đạo hàm \(f'\left( x \right) = x{\left( {x + 2} \right)^2}\left( {{x^2} - x - 2} \right),\,\,\,\forall x \in \,\mathbb{R}\). Hàm số \(f\left( x \right)\) có n điểm cực trị. Tìm n.
Đáp án
Đáp án
Trong không gian \(Oxyz\), cho mặt phẳng \(\left( P \right):\,2x + 2y + z - 1 = 0\). Khoảng cách từ gốc tọa độ \(O\) đến mặt phẳng \(\left( P \right)\) bằng bao nhiêu?
Chỉ điền số nguyên, phân số dạng a/b
Đáp án:
Đáp án:
Một nhóm gồm 2 học sinh lớp 10, 2 học sinh lớp 11 và 2 học sinh lớp 12 xếp thành hai hàng ngang để chụp ảnh, mỗi hàng 3 người. Gọi n là số cách xếp sao cho 2 học sinh lớp 10 đứng ở hàng phía trước và 2 học sinh lớp 12 đứng ở hàng phía sau. Tính n.
Đáp án:
Đáp án:
Cho đa thức \(f\left( x \right)\) thỏa mãn \(\mathop {\lim }\limits_{x \to 1} \dfrac{{f\left( x \right) - 2}}{{x - 1}} = 12\). Tính \(\mathop {\lim }\limits_{x \to 1} \dfrac{{f\left( x \right) - 2}}{{\left( {{x^2} - 1} \right)\left[ {f\left( x \right) + 1} \right]}} \)
Đáp án: \(\mathop {\lim }\limits_{x \to 1} \dfrac{{f\left( x \right) - 2}}{{\left( {{x^2} - 1} \right)\left[ {f\left( x \right) + 1} \right]}} \)
Đáp án: \(\mathop {\lim }\limits_{x \to 1} \dfrac{{f\left( x \right) - 2}}{{\left( {{x^2} - 1} \right)\left[ {f\left( x \right) + 1} \right]}} \)
Một vật được ném lên trên cao và độ cao của nó so với mặt đất được cho bởi công thức \(h\left( t \right) = 3 + 10t - 2{t^2}\left( m \right)\), với \(t\) là thời gian tính bằng giây \(\left( s \right)\) kể từ lúc bắt đầu ném. Độ cao cực đại mà vật đó có thể đạt được so với mặt đất bằng bao nhiêu mét?
Đáp án:
Đáp án:
Gọi k là số giá trị nguyên của tham số \(m\) để hàm số \(y = \dfrac{1}{3}{x^3} - {x^2} \)\(+ \left( {{m^2} - 8m + 16} \right)x - 31\) có cực trị. Tìm k.
Đáp án:
Đáp án:
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Biết các miền \(A\) và \(B\) có diện tích lần lượt là 4 và 1. Tính \(\int\limits_1^2 {4xf\left( {{x^2}} \right)d{\rm{x}}} \)
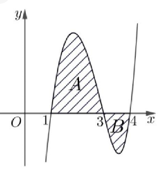
Đáp án: \(\int\limits_1^2 {4xf\left( {{x^2}} \right)d{\rm{x}}} \)
Đáp án: \(\int\limits_1^2 {4xf\left( {{x^2}} \right)d{\rm{x}}} \)
Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:
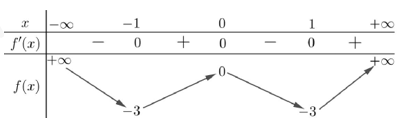
Phương trình \(f\left( {{x^2} - 1} \right) + 1 = 0\) có bao nhiêu nghiệm thực?
Đáp án
Đáp án
Biết rằng tập hợp điểm biểu diễn các số phức \(z\) thỏa mãn \(\left| {\left( {1 + i} \right)z + 5 - i} \right| = 1\) là đường tròn tâm \(I\left( {a;b} \right)\). Tính \(a + b.\)
Đáp án
Đáp án
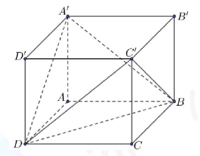
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có đáy \(ABC{\rm{D}}\) là hình vuông cạnh \(a\sqrt 2 \), cạnh bên \(AA' = a\) (minh họa như hình vẽ). Góc giữa hai mặt phẳng \(\left( {A'B{\rm{D}}} \right)\) và \(\left( {C'BD} \right)\) bằng bao nhiêu độ?
Đáp án
$^0$
Đáp án
$^0$
Trong không gian \(Oxyz,\) gọi \(M'\) là điểm đối xứng của điểm \(M\left( {2;0;1} \right)\) qua đường thẳng \(\Delta :\,\,\,\dfrac{x}{1} = \dfrac{{y + 2}}{2} = \dfrac{{z - 1}}{1}\). Tính khoảng cách từ điểm \(M'\) đến mặt phẳng \(\left( {Oxy} \right).\)
Đáp án
Đáp án
Xét các số thực không âm \(a,\,b\) thỏa mãn \(2a + b \le {\log _2}\left( {2a + b} \right) + 1.\) Giá trị nhỏ nhất của \({a^2} + {b^2}\) bằng bao nhiêu?
Đáp án:
Đáp án:
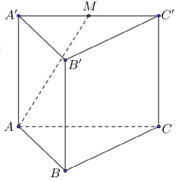
Cho hình lăng trụ tam giác đều \(ABC.A'B'C'\) có độ dài cạnh đáy \(AB = 8,\) cạnh bên bằng \(\sqrt 6 \) (minh họa như hình vẽ). Gọi \(M\) là trung điểm của cạnh \(A'C'\). Khoảng cách từ \(B'\) đến mặt phẳng \(\left( {ABM} \right)\) bằng bao nhiêu?
Đáp án: $d\left(B^{\prime},(A B M)\right)$
Đáp án: $d\left(B^{\prime},(A B M)\right)$
Người ta cần chế tạo các món quà lưu niệm bằng đồng có dạng khối chóp tứ giác đều, được mạ vàng bốn mặt bên và có thể tích bằng \(16 cm^3.\) Diện tích mạ vàng nhỏ nhất của khối chóp bằng bao nhiêu \(cm^2\)? (Kết quả làm tròn đến hàng đơn vị.)
Đáp án
$cm^3$
Đáp án
$cm^3$

