Bất phương trình \(\dfrac{2}{{x + 1}} > \dfrac{5}{{x - 2}}\) có số nghiệm nguyên thuộc đoạn \(\left[ {0;10} \right]\) là
Trả lời bởi giáo viên
Điều kiện: \(\left\{ \begin{array}{l}x \ne - 1\\x \ne 2\end{array} \right..\) Ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,\,\dfrac{2}{{x + 1}} > \dfrac{5}{{x - 2}}\\ \Leftrightarrow \dfrac{2}{{x + 1}} - \dfrac{5}{{x - 2}} > 0\\ \Leftrightarrow \dfrac{{2x - 4 - 5x - 5}}{{\left( {x + 1} \right)\left( {x - 2} \right)}} > 0\\ \Leftrightarrow - \dfrac{{3x + 9}}{{\left( {x + 1} \right)\left( {x - 2} \right)}} > 0\\ \Leftrightarrow \dfrac{{x + 3}}{{\left( {x + 1} \right)\left( {x - 2} \right)}} < 0\end{array}\)
Ta có bảng xét dấu:
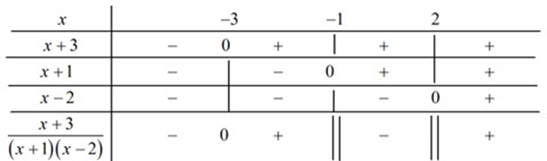
\( \Rightarrow \dfrac{{x + 3}}{{\left( {x + 1} \right)\left( {x - 2} \right)}} < 0 \Leftrightarrow \left[ \begin{array}{l}x < - 3\\ - 1 < x < 2\end{array} \right.\)
Lại có: \(\left\{ \begin{array}{l}x \in \mathbb{Z}\\x \in \left[ {0;\,\,10} \right]\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x \in \mathbb{Z}\\x \in \left[ {0;2} \right)\end{array} \right. \Rightarrow \left[ \begin{array}{l}x = 0\\x = 1\end{array} \right..\)
Vậy bất phương trình có 2 nghiệm nguyên thỏa mãn.
Hướng dẫn giải:
- Chuyển vế, quy đồng.
- Lập BXD và giải bất phương trình, sử dụng quy tắc xét dấu nhị thức bậc nhất: phải cùng trái khác.