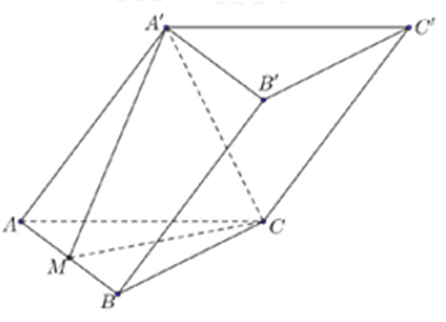
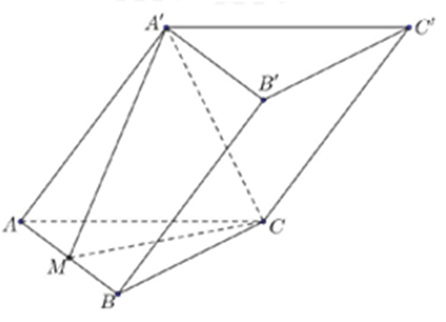
Cho lăng trụ \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác vuông cân tại \(C\). Gọi \(M\) là trung điểm của cạnh\(AB\). Biết rằng \(A'CM\) là tam giác đều cạnh \(a\) và nằm trong mặt phẳng vuông góc với mặt phẳng đáy (minh họa như hình vẽ). Thể tích của khối lăng trụ \(ABC.A'B'C'\) bằng
Trả lời bởi giáo viên
Gọi \(H\) là trung điểm của \(CM\), vì \(\Delta A'CM\) đều cạnh \(a\) nên \(A'H \bot CM\) và \(A'H = \dfrac{{a\sqrt 3 }}{2}\).
Ta có: \(\left\{ \begin{array}{l}\left( {A'CM} \right) \bot \left( {ABC} \right) = CM\\A'H \subset \left( {A'CM} \right),\,\,A'H \bot CM\end{array} \right.\) \( \Rightarrow A'H \bot \left( {ABC} \right)\).
Vì tam giác \(ABC\) vuông cân tại \(C\) nên \(CM = \dfrac{{AC\sqrt 2 }}{2} \Rightarrow AC \)\(= \sqrt 2 CM = a\sqrt 2 = CB\)
\( \Rightarrow {S_{\Delta ABC}} = \dfrac{1}{2}AC.CB \)\(= \dfrac{1}{2}.a\sqrt 2 .a\sqrt 2 = {a^2}\)
Vậy \({V_{ABC.A'B'C'}} = A'H.{S_{\Delta ABC}} = \dfrac{{a\sqrt 3 }}{2}.{a^2} \)\(= \dfrac{{{a^3}\sqrt 3 }}{2}\)
Hướng dẫn giải:
- Gọi \(H\) là trung điểm của \(CM\), chứng minh \(A'H \bot \left( {ABC} \right)\).
- Sử dụng tính chất tam giác vuông cân tính \(CA,\,\,CB\), từ đó tính \({S_{\Delta ABC}}\).
- Tính \({V_{ABC.A'B'C'}} = A'H.{S_{\Delta ABC}}\).