Đề thi tư duy định lượng - Đề số 7

Dựa vào các thông tin được cung cấp dưới đây để trả lời các câu hỏi sau:

Hai tháng đầu năm 2020, lượng khách Quốc tế đến Việt Nam đạt 3,24 triệu lượt người, tăng 4,8% so với cùng kỳ năm trước, đây là mức tăng thấp nhất kể từ năm 2016.

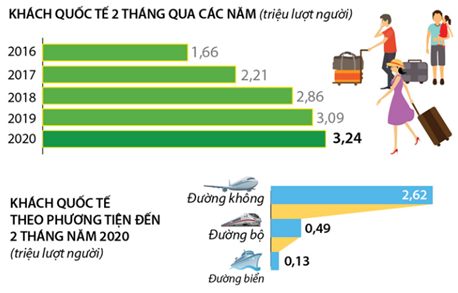
Hai tháng đầu năm 2019, lượng khách quốc tế đến Việt Nam đạt …. triệu lượt người?

Tổng bình phương các nghiệm của phương trình $\sqrt {4{{\rm{x}}^2} + x + 6}  = 4{\rm{x}} - 2 + 7\sqrt {x + 1} $ là:    

Cho hình lăng trụ $ABC.A’B’C’$ có đáy $ABC$ là tam giác vuông cân, $AC = BC = 3a.$ Hình chiếu vuông góc của $B’$ lên mặt đáy trùng với trọng tâm của tam giác $ABC,$ mặt phẳng $(ABB’A’)$ tạo với mặt phẳng $(ABC)$ một góc ${60^0}.$ Tính khoảng cách giữa hai đường thẳng $AB$ và $B’C.$

Khi hệ phương trình $\left\{ \begin{array}{l}x + 2my - z = 1\\2x - my - 2z = 2\\x - \left( {m + 4} \right)y - z = 1\end{array} \right.$ có nghiệm $\left( {x;y;z} \right)$ với $\left\{ \begin{array}{l}m \ne 0\\m \ne  - \dfrac{4}{3}\end{array} \right.$, giá trị $T = 2017x - 2018y - 2017z$ là

Bất phương trình $\dfrac{{3x + 5}}{2} - 1 \le \dfrac{{x + 2}}{3} + x$ có bao nhiêu nghiệm nguyên lớn hơn \( - 10?\)

Trong mặt phẳng với hệ toạ độ $Oxy,$  cho hình vuông $ABCD$  biết  $M\left( {2;1} \right);N\left( {4;-2} \right);P\left( {2;0} \right);Q\left( {1;2} \right)$  lần lượt thuộc cạnh $AB,BC,CD,AD.$  Hãy lập phương trình  cạnh $AB$  của hình vuông.

Phương trình đường tròn $(C)$ đi qua hai điểm \(A(0;1),B(1;0)\) và có tâm nằm trên đường thẳng: \(x + y + 2 = 0\) là:

Nghiệm của phương trình \(\sin 3x = \cos x\) là:

Một người làm việc cho một công ty. Theo hợp đồng trong năm đầu tiên, tháng lương thứ nhất là 6 triệu đồng và lương tháng sau cao hơn tháng trước là 200 ngàn đồng. Hỏi theo hợp đồng tháng thứ 7 người đó nhận được lương là bao nhiêu?

Cho 10 điểm trong không gian, trong đó không có 3 điểm nào thẳng hàng. Nếu trong 10 điểm trên không có 4 điểm nào đồng phẳng thì có bao nhiêu tứ diện được tạo thành?

Mỗi đề thi có $5$ câu được chọn ra từ $100$ câu có sẵn. $1$ học sinh học thuộc $80$ câu. Tính xác suất để học sinh rút ngẫu nhiên ra $1$ đề thi có $4$ câu đã học thuộc.

Cho đa thức \(f\left( x \right)\) thỏa mãn \(\mathop {\lim }\limits_{x \to 1} \dfrac{{f\left( x \right) - 5}}{{x - 1}} = 10\). Tính \(L = \mathop {\lim }\limits_{x \to 1} \dfrac{{\sqrt {f\left( x \right) + 4}  - 3}}{{x - 1}}\).

Tính đạo hàm của hàm số \(y = \dfrac{{\sin 2x + 2}}{{\cos 2x + 3}}\).

Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Gọi \(M\) là trung điểm \(SD\), \(N\) là trọng tâm tam giác \(SAB\). Đường thẳng \(MN\) cắt mặt phẳng \(\left( {SBC} \right)\) tại điểm \(I\). Tính tỷ số \(\dfrac{{IN}}{{IM}}\).

Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(B\), \(AB = a\), \(BC = 2a\), \(SA\) vuông góc với mặt phẳng đáy và \(SA = \sqrt {15} a\) (tham khảo hình bên)

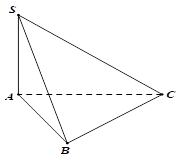
Góc giữa đường thẳng \(SC\) và mặt phẳng đáy bằng

Tìm nguyên hàm của hàm số  \(f(x) = {x^2} + \dfrac{2}{{{x^2}}}.\) 

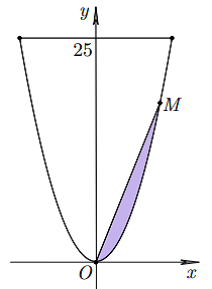
Ông B có một khu vườn giới hạn bởi đường parabol và một đường thẳng. Nếu đặt trong hệ tọa độ $Oxy$ như hình vẽ bên thì parabol có phương trình $y = {x^2}$và đường thẳng là $y = 25$. Ông B dự định dùng một mảnh vườn nhỏ được chia từ khu vườn bởi đường thẳng đi qua $O$ và điểm $M$ trên parabol để trồng hoa. Hãy giúp ông B xác định điểm $M$ bằng cách tính độ dài $OM$ để diện tích mảnh vường nhỏ bằng $\dfrac{9}{2}$.

Cho \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) thỏa mãn \(f\left( x \right) = f\left( {2020 - x} \right)\) và \(\int\limits_3^{2017} {f\left( x \right)dx}  = 4\). Khi đó \(\int\limits_3^{2017} {xf\left( x \right)dx} \) bằng:

Cho \(\int\limits_0^1 {\left( {1 + 3x} \right)f'\left( x \right)dx}  = 2019;\) \(4f\left( 1 \right) - f\left( 0 \right) = 2020.\) Tính \(\int\limits_0^{\frac{1}{3}} {f\left( {3x} \right)dx.} \)

Cho vật thể \(V\) được giới hạn bởi hai mặt phẳng \(x = 0\) và \(x =  - 2\), mặt phẳng vuông góc với trục \(Ox\) cắt \(V\) theo thiết diện \(S\left( x \right) = 2{x^2}\). Thể tích của \(V\) được tính bởi:

Anh A mua chiếc điện thoại giá 18.500.000 đồng nhưng chưa đủ tiền nên anh đã quyết định chọn mua hình thức trả góp và trả trước 5 triệu đồng trong 12 tháng, với lãi suất là 3,4%/tháng. Hỏi mỗi tháng anh A sẽ phải trả cho cửa hàng số tiền là bao nhiêu?

Tìm số nghiệm nguyên của bất phương trình \({\left( {\dfrac{1}{5}} \right)^{{x^2} - 2x}} \ge \dfrac{1}{{125}}\)

Nghiệm của bất phương trình ${\log _2}(x + 1) + {\log _{\frac{1}{2}}}\sqrt {x + 1}  \le 0$ là :

Tìm tập hợp tất cả các tham số $m$ sao cho phương trình ${4^{{x^2} - 2x + 1}} - m{.2^{{x^2} - 2x + 2}} + 3m - 2 = 0$ có 4 nghiệm phân biệt.

Đồ thị hàm số $y = {x^3} - \left( {3m + 1} \right){x^2} + \left( {{m^2} + 3m + 2} \right)x + 3$ có điểm cực tiểu và điểm cực đại nằm về hai phía của trục tung khi:

Tìm giá trị lớn nhất \(M\) và giá trị nhỏ nhất \(m\) của hàm số \(y = f\left( x \right) = {x^2} - 4x + 3\) trên đoạn \(\left[ { - 2;1} \right]\)

Cho hình chóp $S.ABCD$ có cạnh \(SA = x\) còn tất cả các cạnh khác có độ dài bằng 2. Tính thể tích \(V\) lớn nhất của khối chóp S.ABCD.

Cho số phức z thỏa mãn \(2iz + \overline z  = 1 - i\). Phần thực của số phức \(z\) là:

Xét các số phức z thỏa mãn \(\left( {z + 2i} \right)\left( {\overline z  + 2} \right)\) là số thuần ảo. Biết rằng tập hợp tất cả các điểm biểu diễn của z là một đường tròn, tâm của đường tròn đó có tọa độ là:

Cho số phức \(z\) thỏa mãn \(\left| {z + i} \right| = 1\). Biết rằng tập hợp các điểm biểu diễn số phức \(w = \left( {3 + 4i} \right)z + 2 + i\) là một đường tròn tâm \(I\), điểm \(I\) có tọa độ là $I(a;b)$, tính $a-b$

Trong mặt phẳng tọa độ Oxy cho các điểm A, B như hình vẽ bên.

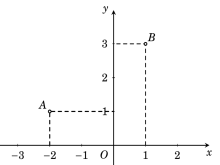
Trung điểm của đoạn thẳng AB biểu diễn số phức

Trong không gian $Oxyz$, cho ba điểm $A\left( {1,0,0} \right),B\left( {0,1,0} \right)$ và $C\left( {0,0,1} \right)$ . Phương trình mặt phẳng $\left( P \right)$  đi qua ba điểm $A,B,C$ là:

Đề thi THPT QG - 2021 - mã 103

Trong không gian \(Oxyz\), cho hai điểm \(A\left( {0;0;1} \right)\) và \(B\left( {1;2;3} \right)\). Mặt phẳng đi qua \(A\) và vuông góc với \(AB\) có phương trình là:

Trong không gian Oxyz, điểm N đối xứng với \(M(3; - 1;2)\) qua trục Oy là

Trong không gian \(Oxyz,\)  cho biết có hai mặt cầu có tâm nằm trên đường thẳng \(d:\dfrac{x}{2} = \dfrac{{y - 1}}{1} = \dfrac{{z + 2}}{{ - 1}},\) tiếp xúc đồng thời với hai mặt phẳng \(\left( \alpha  \right):x + 2y - 2z + 1 = 0\)  và\(\left( \beta  \right):2x - 3y - 6z - 2 = 0\) . Gọi \({R_1};{R_2}\left( {{R_1} > {R_2}} \right)\)  là bán kính của hai mặt cầu đó. Tỉ số \(\dfrac{{{R_1}}}{{{R_2}}}\)  bằng

Hình chiếu của điểm \(M\left( {0;2;1} \right)\) trên mặt phẳng \(\left( {Oxy} \right)\) thuộc:

Trong không gian với hệ tọa độ $Oxyz$,  cho tứ diện \(ABCD\)  có \(A(2; - 1;1)\), \(B(3;0; - 1)\), \(C(2; - 1;3)\) và $D$ thuộc trục $Oy$ . Tính tổng tung độ của các điểm $D$, biết thể tích tứ diện bằng $5$ .

Trong không gian với hệ trục tọa độ \(Oxyz\), hãy tính \(p\) và \(q\) lần lượt là khoảng cách từ điểm \(M\left( {5; - 2;0} \right)\) đến mặt phẳng \(\left( {Oxz} \right)\) và mặt phẳng \(\left( P \right):\,\,3x - 4z + 5 = 0\).

Trong không gian với hệ tọa độ $Oxyz$, cho mặt phẳng \((P):x - y - z - 1 = 0\) và đường thẳng $d:\dfrac{{x + 1}}{2} = \dfrac{{y - 1}}{1} = \dfrac{{z - 2}}{3}$.   Phương trình đường thẳng \(\Delta \)  qua \(A(1;1; - 2)\) vuông góc với $d$ và song song với $(P)$ là:

Trong không gian tọa độ \(\left( {Oxyz} \right)\), cho các điểm \(A\left( {0;0;1} \right),B\left( {1; - 1;2} \right),\)\(D\left( { - 3; - 2; - 1} \right),A'\left( {1;1;1} \right)\). Thể tích khối hộp \(ABCD.A'B'C'D'\) là:

Cho hình lăng trụ \(ABCD.A'B'C'D'\) có đáy $ABCD$ là hình chữ nhật với \(AB = \sqrt 3 ,AD = \sqrt 7 \). Hai mặt bên $\left( {ABB'A'} \right)$  và $\left( {ADD'A'} \right)$  lần lượt tạo với đáy những góc \({45^0}\) và \({60^0}\). Tính thể tích khối hộp nếu biết cạnh bên bằng $1$.

Hàm số $y =  - {x^4} - 2{x^2} + 3$ nghịch biến trên:

Hàm số $y = {x^3} - 3x^2 + 4$ đạt cực tiểu tại:

Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = \left( {{x^2} - 1} \right){\left( {x + 2} \right)^3}\), \(\forall x \in \mathbb{R}\). Hàm số có bao nhiêu điểm cực trị?

Gọi k là số giá trị nguyên của tham số \(m\) để hàm số \(y = \dfrac{1}{3}{x^3} - {x^2} \)\(+ \left( {{m^2} - 8m + 16} \right)x - 31\) có cực trị. Tìm k.

Một khối chóp tam giác có cạnh đáy bằng 6, 8, 10. Một cạnh bên có độ dài bằng \(4\) và tạo với đáy góc \({60^0}\). Thể tích của khối chóp đó là:

Cho hàm số $y = {x^4} - 2(m + 1){x^2} + m + 2$ có đồ thị $\left( C \right)$. Gọi $\Delta $ là tiếp tuyến với đồ thị $\left( C \right)$ tại điểm thuộc $\left( C \right)$ có hoành độ bằng $1$. Với giá trị nào của tham số $m$ thì $\Delta $ vuông góc với đường thẳng $d:y =  - \dfrac{1}{4}x - 2016$

Cho hai số thực $a$, $b$ thỏa mãn $a > b > \dfrac{4}{3}$ và biểu thức $P = 16{\log _a}\left( {\dfrac{{{a^3}}}{{12b - 16}}} \right) + 3\log _{\frac{a}{b}}^2a$ có giá trị nhỏ nhất. Tính $a + b.$

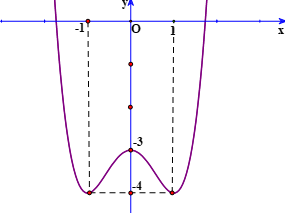
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ sau. Có bao nhiêu giá trị nguyên của \(m\) để phương trình \(f\left( {\sin x} \right) = m\) có đúng hai  nghiệm trên đoạn \(\left[ {0;\pi } \right]\).

Tìm giá trị lớn nhất của hàm số \(y = f\left( x \right) = \sqrt {x - 1}  + \sqrt {5 - x} \) trên đoạn \(\left[ {1;5} \right]\).