Cho hình chóp $S.ABCD$ có cạnh \(SA = x\) còn tất cả các cạnh khác có độ dài bằng 2. Tính thể tích \(V\) lớn nhất của khối chóp S.ABCD.
Trả lời bởi giáo viên
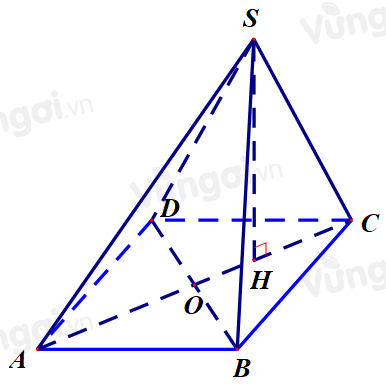
Bước 1: Gọi \(O\) là giao điểm của AC và BD. Chứng minh tam giác SAC vuông tại S.
Gọi \(O\) là giao điểm của AC và BD .
Ta có \(\Delta BAD = \Delta BSD = \Delta BCD\) nên \(AO = SO = CO\)
\( \Rightarrow SO = \dfrac{1}{2}AC\) \( \Rightarrow \Delta SAC\) vuông tại \(S\).
Bước 2: Biểu diễn AC, OD, BD theo x.
Do đó, \(AC = \sqrt {S{A^2} + S{C^2}} = \sqrt {{x^2} + 4} \)
\( \Rightarrow OD = \sqrt {A{D^2} - A{O^2}} = \sqrt {4 - \dfrac{{4 + {x^2}}}{4}} = \dfrac{{\sqrt {12 - {x^2}} }}{2}\)
\( \Rightarrow BD = \sqrt {12 - {x^2}} ,0 < x < 2\sqrt 3 .\)
Bước 3: Trong \(\Delta SAC\) hạ \(SH \bot AC\). Chứng minh \(SH \bot \left( {ABCD} \right)\)
Ta thấy \(\left\{ {\begin{array}{*{20}{l}}{BD \bot AC}\\{BD \bot SO}\end{array} \Rightarrow BD \bot (SAC)} \right.\).
Trong \(\Delta SAC\) hạ \(SH \bot AC\).
Khi đó, \(\left\{ {\begin{array}{*{20}{l}}{SH \bot AC}\\{SH \bot BD}\end{array} \Rightarrow SH \bot (ABCD)} \right.\).
Bước 4: Lập phương trình dựa vào hệ thức lượng trong tam giác vuông SAC, tìm x.
Xét tam giác vuông SAC có \(\dfrac{1}{{S{H^2}}} = \dfrac{1}{{S{A^2}}} + \dfrac{1}{{S{C^2}}}\)
\( \Rightarrow SH = \dfrac{{SA.SC}}{{\sqrt {S{A^2} + S{C^2}} }} = \dfrac{{2x}}{{\sqrt {4 + {x^2}} }}\)
\( \Rightarrow {V_{S.ABCD}} = \dfrac{1}{3} \cdot \dfrac{1}{2}\sqrt {{x^2} + 4} \cdot \sqrt {12 - {x^2}} \cdot \dfrac{{2x}}{{\sqrt {{x^2} + 4} }}\)
\( = \dfrac{1}{3}x.\sqrt {12 - {x^2}} \le \dfrac{1}{3}\dfrac{{{x^2} + 12 - {x^2}}}{2} = 2\)
Dấu "=" xảy ra khi và chỉ khi \({x^2} = 12 - {x^2} \Rightarrow x = \sqrt 6 \).
Hướng dẫn giải:
Bước 1: Gọi \(O\) là giao điểm của AC và BD. Chứng minh tam giác SAC vuông tại S.
Bước 2: Biểu diễn AC, OD, BD theo x.
Bước 3: Trong \(\Delta SAC\) hạ \(SH \bot AC\). Chứng minh \(SH \bot \left( {ABCD} \right)\)
Bước 4: Lập phương trình dựa vào hệ thức lượng trong tam giác vuông SAC, tìm x.