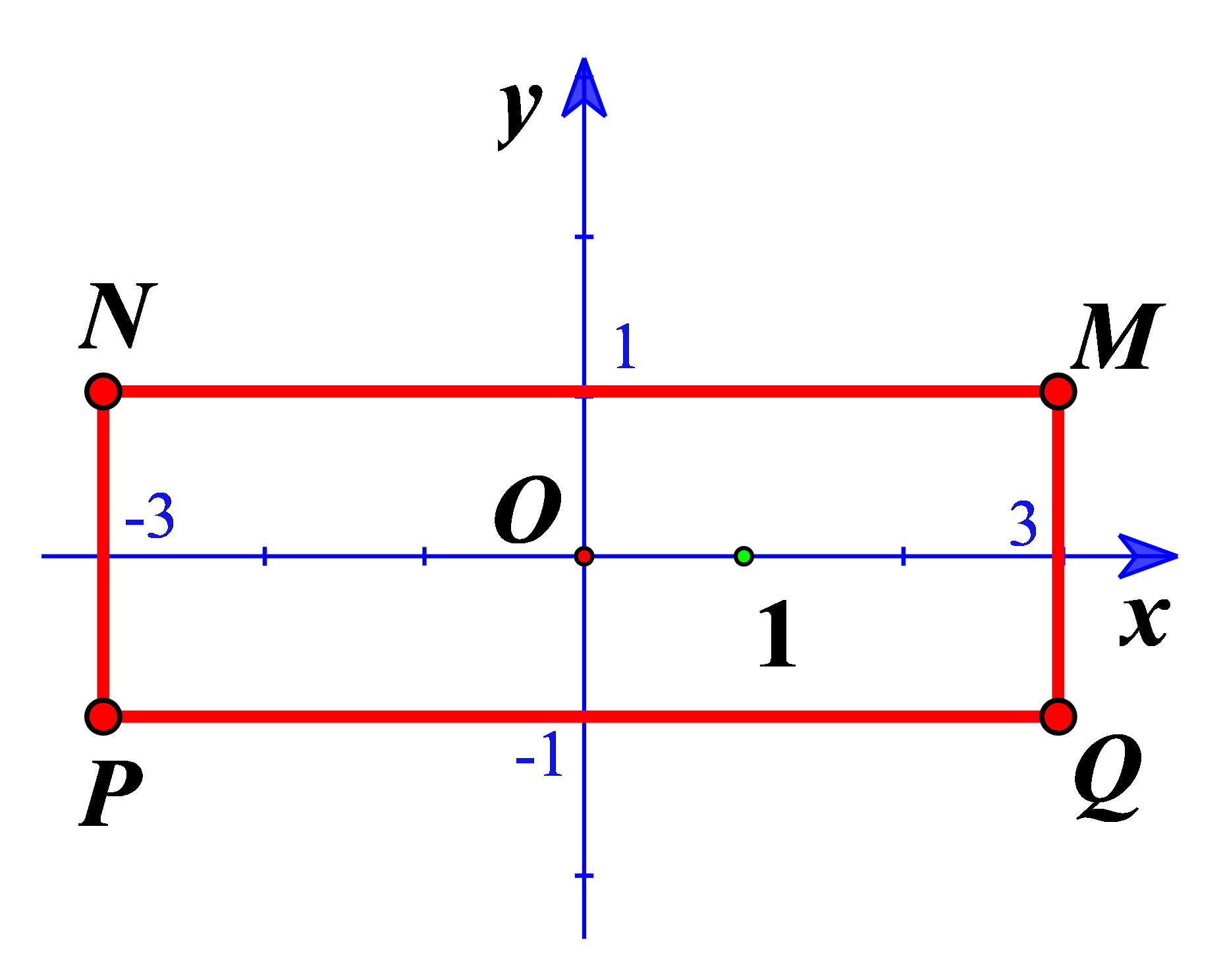
Gọi \({z_1}\) là nghiệm phức có phần ảo âm của phương trình \({z^2} - 2z + 5 = 0\). Hỏi điểm biểu diễn của \(w = (1 + i){z_1}\) là điểm nào trong các điểm trong các điểm M, N, P, Q ở hình bên?

\(4,2\% \)

\(4,26\% \)

\(4,3\% \)

\(4,5\% \)

$\left[ \begin{array}{l}m = 1\\m = 2\end{array} \right.$      

$\left[ \begin{array}{l}m < 1\\m > 2\end{array} \right.$

$1 < m < 2$

Không xác định được

$\dfrac{a}{{\sqrt 3 }}.$ 

$\dfrac{{2a}}{{\sqrt 3 }}.$

$\dfrac{a}{3}.$

$\dfrac{{\sqrt{3}a}}{2}.$

\(\left( {x;y} \right) = \left( { - 3 - \sqrt 3 ; - 2 + \sqrt 3 } \right)\) \(\left( {x;y} \right) = \left( { - 3 + \sqrt 3 ; - 2 - \sqrt 3 } \right)\).

\(\left( {x;y} \right) = \left( { - 3 - \sqrt 3 ; - 3 + \sqrt 3 } \right);\) \(\left( {x;y} \right) = \left( { - 2 - \sqrt 3 ; - 2 + \sqrt 3 } \right)\).

\(\left( {x;y} \right) = \left( { - 3; - 2} \right);\) \(\left( {x;y} \right) = \left( {3;2} \right)\)

\(\left( {x;y} \right) = \left( { - 3;3} \right);\) \(\left( {x;y} \right) = \left( {2;2} \right)\).

\(x \in \left[ { - \dfrac{1}{3};\dfrac{1}{3}} \right].\)

\(x \in \left( { - \infty ; - \dfrac{1}{3}} \right) \cup \left( {\dfrac{1}{3}; + \infty } \right).\)

\(x \in \left( { - \infty ; - \dfrac{1}{3}} \right] \cup \left[ {\dfrac{1}{3}; + \infty } \right).\)

\(x \in \left( { - \dfrac{1}{3};\dfrac{1}{3}} \right).\)

\({(x - 2)^2} + {(y - 1)^2} = 17\)

\({(x - 2)^2} + {(y - 1)^2} = 2\sqrt 5 \)

\({(x - 4)^2} + {(y - 2)^2} = 17\)

\({(x + 2)^2} + {(y + 1)^2} = 17\)