Cho hàm số $y = x + \dfrac{1}{x}.$ Giá trị nhỏ nhất của hàm số trên khoảng $\left( {0;\, + \infty } \right)$ là:
Trả lời bởi giáo viên
TXĐ: \(R\backslash \left\{ 0 \right\}\)
$y' = 1 - \dfrac{1}{{{x^2}}} = \dfrac{{{x^2} - 1}}{{{x^2}}}$
$y' = 0 \Leftrightarrow \dfrac{{{x^2} - 1}}{{{x^2}}} = 0 \Leftrightarrow {x^2} - 1 = 0 \Leftrightarrow x=1 (tm) $ hoặc $x=-1 (ktm)$
Bảng biến thiên:
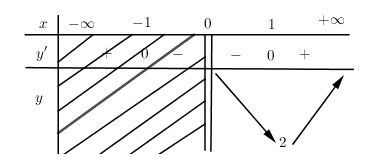
$ \Rightarrow \mathop {Min}\limits_{x \in \left( {0; + \infty } \right)} \,y = f\left( 1 \right) = 2$
Hướng dẫn giải:
- Bước 1: Tính $f'\left( x \right)$, giải phương trình $y' = 0$ tìm các nghiệm ${x_1},{x_2},...{x_n}$ thỏa mãn $a \leqslant {x_1} < {x_2} < ... < {x_n} \leqslant b$.
- Bước 2: Tính các giá trị $f\left( {{x_1}} \right),f\left( {{x_2}} \right),...,f\left( {{x_n}} \right)$ và $A = \mathop {\lim }\limits_{x \to {a^ + }} f\left( x \right);B = \mathop {\lim }\limits_{x \to {b^ - }} f\left( x \right)$.
- Bước 3: So sánh các giá trị tính được và kết luận.
Giải thích thêm:
Nhìn vào bảng biến thiên ta thấy GTNN của hàm số là $y = 2$ nên chúng ta không cần thiết phải tính các giới hạn tại $x = 0$ và $x = + \infty $
Câu hỏi khác
Cho biểu thức \(f\left( x \right) = 9{x^2} - 1.\) Tập hợp tất cả các giá trị của \(x\) để \(f\left( x \right) < 0\) là
\(x \in \left( { - \infty ; - \dfrac{1}{3}} \right) \cup \left( {\dfrac{1}{3}; + \infty } \right).\)
- Đề thi tư duy định lượng - Đề số 1 đánh giá năng lực ĐHQG Hà Nội có lời giải chi tiết
- Đề thi tư duy định lượng - Đề số 2 đánh giá năng lực ĐHQG Hà Nội có lời giải chi tiết
- Đề thi tư duy định lượng - Đề số 4 đánh giá năng lực ĐHQG Hà Nội có lời giải chi tiết
- Đề thi tư duy định lượng - Đề số 11 đánh giá năng lực ĐHQG Hà Nội có lời giải chi tiết
- Đề thi tư duy định lượng - Đề số 5 đánh giá năng lực ĐHQG Hà Nội có lời giải chi tiết
