Cho tứ diện $OABC$ có ba cạnh $OA,\,\,OB,\,\,OC$ đôi một vuông góc với nhau. Biết khoảng cách từ điểm $O$ đến các đường thẳng $BC,\,\,CA,\,\,AB$ lần lượt là $a,\,\,a\sqrt 2 ,\,\,a\sqrt 3$. Khoảng cách từ điểm $O$ đến mặt phẳng $\left( {ABC} \right)$ là $\dfrac{{2a\sqrt {m} }}{{11}}$. Tìm $m$.

Đáp án:

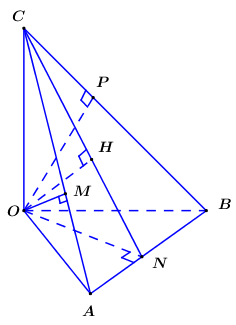
Bước 1: Kẻ $OM \bot AC\,\,\left( {M \in AC} \right)$, $ON \bot AB\,\,\left( {N \in AB} \right)$, $OP \bot BC\,\,\left( {P \in BC} \right)$.

Kẻ $OM \bot AC\,\,\left( {M \in AC} \right)$, $ON \bot AB\,\,\left( {N \in AB} \right)$, $OP \bot BC\,\,\left( {P \in BC} \right)$.

Khi đó ta có $OP = a,\,\,OM = a\sqrt 2 ,\,\,ON = a\sqrt 3$.

Bước 2: Trong $\left( {OCN} \right)$ kẻ $OH \bot CN\,\,\left( {H \in CN} \right)$, chứng minh $OH \bot \left( {ABC} \right)$.

Trong $\left( {OCN} \right)$ kẻ $OH \bot CN\,\,\left( {H \in CN} \right)$ ta có:

$\begin{array}{l}\left\{ \begin{array}{l}AB \bot ON\\AB \bot OC\end{array} \right. \Rightarrow AB \bot \left( {OCN} \right) \Rightarrow AB \bot OH\\\left\{ \begin{array}{l}OH \bot AB\\OH \bot CN\end{array} \right. \Rightarrow OH \bot \left( {ABC} \right) \Rightarrow d\left( {O;\left( {ABC} \right)} \right) = OH\end{array}$

Bước 3: Sử dụng hệ thức lượng trong tam giác vuông để tính khoảng cách.

Áp dụng hệ thức lượng trong tam giác vuông ta có: $\dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{C^2}}} + \dfrac{1}{{O{N^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} + \dfrac{1}{{O{C^2}}}$

Lại có

$\begin{array}{l}\dfrac{1}{{O{M^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{C^2}}};\,\,\dfrac{1}{{O{N^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}};\,\,\dfrac{1}{{O{P^2}}} = \dfrac{1}{{O{B^2}}} + \dfrac{1}{{O{C^2}}}\\ \Rightarrow \dfrac{1}{{O{M^2}}} + \dfrac{1}{{O{N^2}}} + \dfrac{1}{{O{P^2}}} = 2\left( {\dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} + \dfrac{1}{{O{C^2}}}} \right)\\ \Rightarrow \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} + \dfrac{1}{{O{C^2}}} = \dfrac{1}{2}\left( {\dfrac{1}{{O{M^2}}} + \dfrac{1}{{O{N^2}}} + \dfrac{1}{{O{P^2}}}} \right)\\ \Rightarrow \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} + \dfrac{1}{{O{C^2}}} = \dfrac{1}{2}\left( {\dfrac{1}{{2{a^2}}} + \dfrac{1}{{3{a^2}}} + \dfrac{1}{{{a^2}}}} \right) = \dfrac{{11}}{{12{a^2}}}\\ \Rightarrow \dfrac{1}{{O{H^2}}} = \dfrac{{11}}{{12{a^2}}} \Rightarrow OH = \dfrac{{2a\sqrt {33} }}{{11}}\end{array}$

=> $d\left( {O;\left( {ABC} \right)} \right) = \dfrac{{2a\sqrt {33} }}{{11}}$.

Vậy m=33.