Hàm số \(y = \left( {{x^2} - 1} \right){\left( {3x - 2} \right)^3}\) có bao nhiêu điểm cực đại?
Đáp án:
Trả lời bởi giáo viên
Đáp án:
Bước 1: Giải phương trình \(f'\left( x \right) = 0\).
+ \(y' = {\left( {3x - 2} \right)^2}\left( {15{x^2} - 4x - 9} \right)\)
+ \(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{2}{3}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {nghiem\,\,boi\,\,chan} \right)\\x = \dfrac{{2 + \sqrt {139} }}{{15}}\,\,\,\,\left( {nghiem\,\,boi\,\,le} \right)\\x = \dfrac{{2 - \sqrt {139} }}{{15}}\,\,\,\,\left( {nghiem\,\,boi\,\,le} \right)\end{array} \right.\)
Bước 2: Lập BBT của hàm số từ đó xác định điểm cực đại của hàm số.
\( \Rightarrow \) BBT:
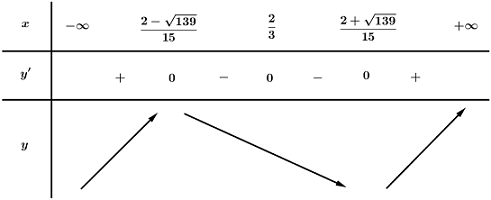
\( \Rightarrow \) Hàm số có 1 điểm cực đại
Hướng dẫn giải:
Bước 1: Giải phương trình \(f'\left( x \right) = 0\).
Bước 2: Lập BBT của hàm số từ đó xác định điểm cực đại của hàm số.
Câu hỏi khác
- Đề thi tư duy định lượng - Đề số 1 đánh giá năng lực ĐHQG Hà Nội có lời giải chi tiết
- Đề thi tư duy định lượng - Đề số 2 đánh giá năng lực ĐHQG Hà Nội có lời giải chi tiết
- Đề thi tư duy định lượng - Đề số 4 đánh giá năng lực ĐHQG Hà Nội có lời giải chi tiết
- Đề thi tư duy định lượng - Đề số 5 đánh giá năng lực ĐHQG Hà Nội có lời giải chi tiết
- Đề thi tư duy định lượng - Đề số 11 đánh giá năng lực ĐHQG Hà Nội có lời giải chi tiết
